P1930

[USACO3.3] 亚瑟王的宫殿

题目描述

很久以前，亚瑟王和他的骑士习惯每年元旦去庆祝他们的友谊。为了纪念上述事件， 我们把这些故事看作是一个棋盘游戏。有一个国王和若干个骑士被放置在一个由许多方格 组成的棋盘上，没有两个骑士在同一个方格内。

这个例子是标准的 \(8\times 8\) 棋盘。

国王可以移动到任何一个相邻的方格，从下图中黑子位置到下图中白子位置前提是他 不掉出棋盘之外。

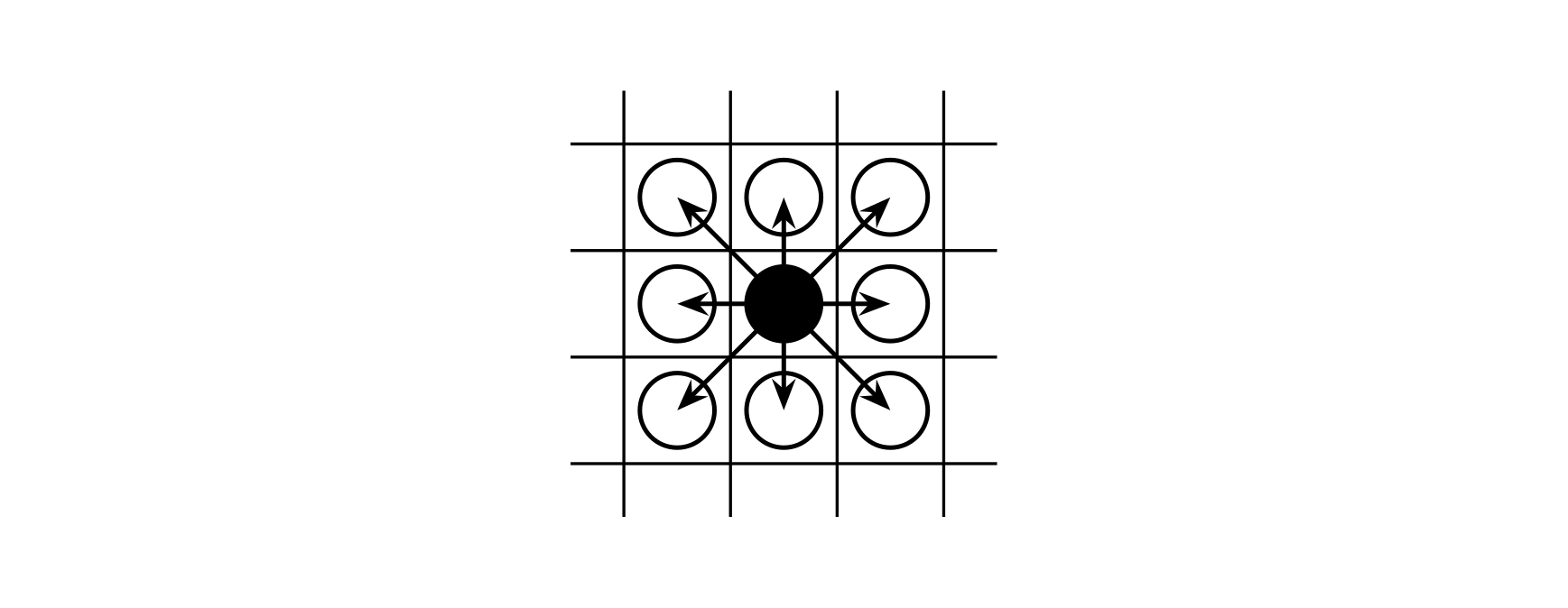
一个骑士可以从下图中黑子位置移动到下图中白子位置(走“日”字形） 但前提是他 不掉出棋盘之外。

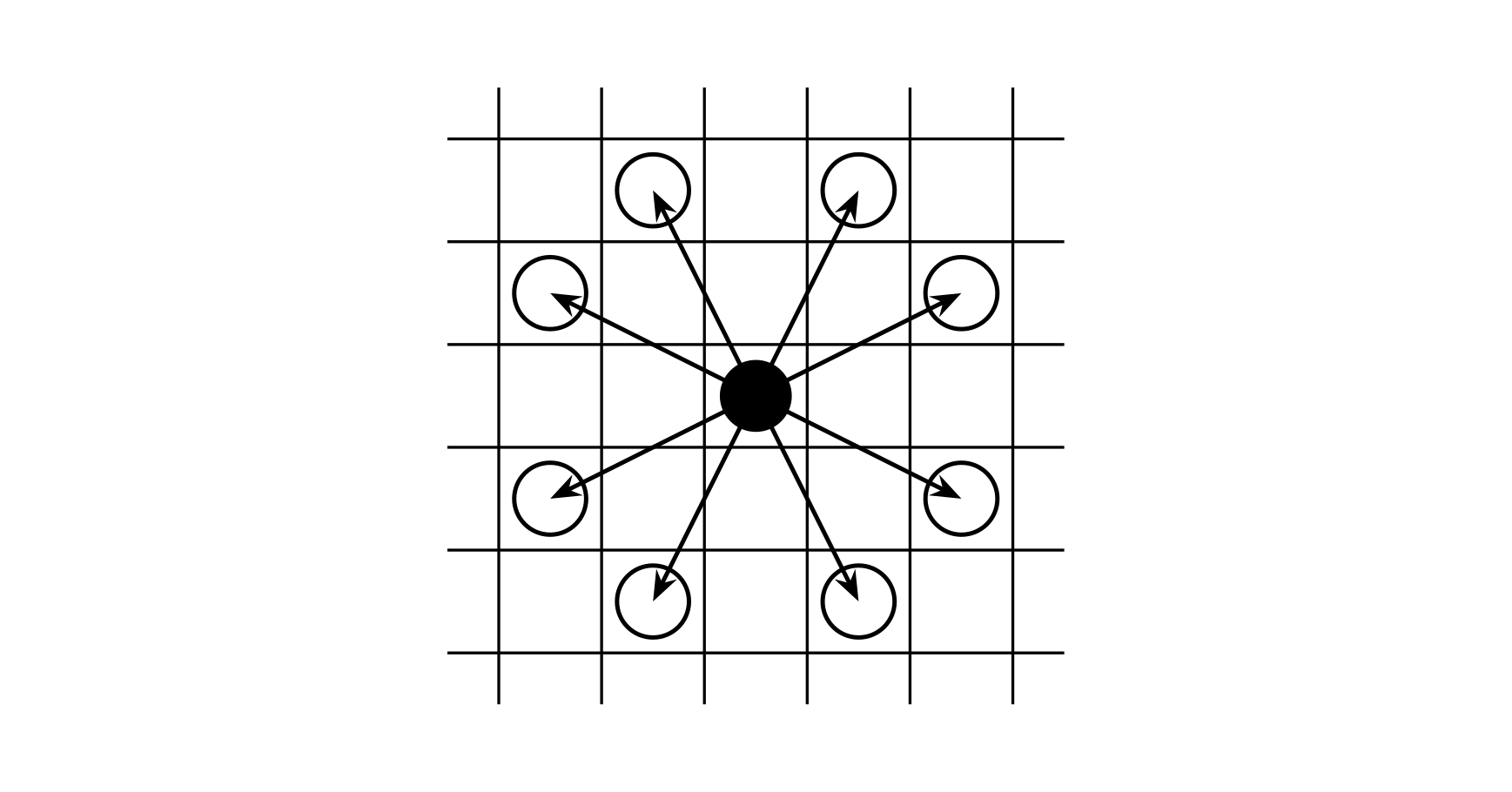
在游戏中，玩家可在每个方格上放不止一个棋子，假定方格足够大，任何棋子都不会 阻碍到其他棋子正常行动。

玩家的任务就是把所有的棋子移动到同一个方格里——用最小的步数。为了完成这个 任务，他必须按照上面所说的规则去移动棋子。另外，玩家可以选择一个骑士跟国王从他们两个相遇的那个点开始一起行动，这时他们按照骑士的行动规则行动，其他的单独骑士则自己一直走到集中点。骑士和国王一起走的时候，只算一个人走的步数。

请计算他们集中在一起的最小步数，而且玩家必须自己找出这个集中点。当然，这些 棋子可以在棋盘的任何地方集合。

输入格式

第一行：两个用空格隔开的整数：\(R,C\) 分别为棋盘行和列的长。不超过 \(26\) 列，\(40\) 行。

---

这道题我没有做出来，丢脸 つ﹏⊂死因是因为我一直想的是枚举一个接到国王的中转点，再枚举哪个骑士最好去救国王。这显然是很难做的很优秀的。

当时一直想的是：怎么样加快求出就国王的骑士最少能走多少。这似乎很难，其实应该可以引申出一个有意思的问题：走日从 \((0, 0)\) 到 \((x, y)\) 的最小步数。应该有数学推导式子，然后可以利用数学式子的特征加速。但是我并不知道这个问题怎么做，有没有巨神教教呢 qwq

因此就不要在这个死胡同里面兜圈子了。可以直接设 \(d(x, y, 0/1)\) 代表骑士在 \((x, y)\) 位置，有没有搭载上国王即可。转移显然，枚举终点时间复杂度 \(O(n^2m^2)\) 显然能过。

也许这个可以看成思维“往后退一步”。 比如我现在求出中转点，目的是为了求出一个最近的骑士能够搭载国王。再退一步，就是求哪个骑士能够在搭载上国王之后到集合点步数最少。这个是不用使用过于精细的做法的，一个极为简单的 dp 就行。

还是要多看看呐

#include <bits/stdc++.h>
using namespace std;
const int N = 50, inf = N * N * 2;
const int dx[9] = {1, -1, 1, -1, 2, -2, 2, -2};
const int dy[9] = {2, -2, -2, 2, 1, -1, -1, 1};
int Abs(int x) {
	return max(x, -x);
}
int n, m, kx, ky;
bool judge(int x, int y) {
	return ((x >= 1 && x <= n) && (y >= 1 && y <= m));
}
int dis[N + 10][N + 10][2];
bool vis[N + 10][N + 10][2];
struct node {
	int x, y, opt, val;
	node(int X, int Y, int O, int V) {
		x = X, y = Y, opt = O, val = V;
	}
	bool operator < (const node &other) const {
		return val > other.val;
	}
};
void bfs(int sx, int sy) {
	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= m; j++) {
			dis[i][j][0] = dis[i][j][1] = inf;
			vis[i][j][0] = vis[i][j][1] = 0;
		}

	dis[sx][sy][0]= 0 ;
	priority_queue <node> que;
	que.push(node(sx, sy, 0, 0));
	while(!que.empty()) {
		node fr = que.top(); que.pop();
		int x = fr.x, y = fr.y, w = fr.opt;
		if(vis[x][y][w]) continue;
		vis[x][y][w] = 1;

		if(!w) {
			if(dis[x][y][1] > dis[x][y][0] + max(Abs(x - kx), Abs(y - ky))) {
				dis[x][y][1] = dis[x][y][0] + max(Abs(x - kx), Abs(y - ky));
				que.push(node(x, y, 1, dis[x][y][1]));
			}
		}
		for(int i = 0; i < 8; i++) {
			int xx = x + dx[i];
			int yy = y + dy[i];
			if(!judge(xx, yy)) continue;

			if(dis[xx][yy][w] > dis[x][y][w] + 1) {
				dis[xx][yy][w] = dis[x][y][w] + 1;
				que.push(node(xx, yy, w, dis[xx][yy][w]));
			}
		}
	}
}
vector <node> knt;
int solve(int sx, int sy) {
	bfs(sx, sy);
	
	int sum = 0, minn = inf;
	for(int i = 0; i < knt.size(); i++) {
		int x = knt[i].x, y = knt[i].y;
		sum += dis[x][y][0];
		minn = min(minn, dis[x][y][1] - dis[x][y][0]);
	}

	return min(sum + max(Abs(sx - kx), Abs(sy - ky)), sum + minn);
}

int main() {
	cin >> m >> n;
	char tmp; cin >> tmp >> ky;
	kx = tmp - 'A' + 1;
	int t;
	while(cin >> tmp >> t)
		knt.push_back(node(tmp - 'A' + 1, t, 0, 0));

	int minn = inf;
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= m; j++)
			minn = min(minn, solve(i, j));
	}
	cout << minn << endl;
}