深度学习的激活函数 ：sigmoid、tanh、ReLU 、Leaky Relu、RReLU、softsign 、softplus、GELU

深度学习的激活函数  ：sigmoid、tanh、ReLU 、Leaky Relu、RReLU、softsign 、softplus、GELU

2019-05-06 17:56:43 wamg潇潇 阅读数 652更多

分类专栏： python机器学习 深度学习

 

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/qq_29831163/article/details/89887655

  【 tensorflow中文文档：tensorflow 的激活函数有哪些】

激活函数可以分为两大类 ：

• 饱和激活函数： sigmoid、 tanh
• 非饱和激活函数: ReLU 、Leaky Relu   、ELU【指数线性单元】、PReLU【参数化的ReLU 】、RReLU【随机ReLU】

相对于饱和激活函数，使用“非饱和激活函数”的优势在于两点：
    1.首先，“非饱和激活函数”能解决深度神经网络【层数非常多！！】的“梯度消失”问题，浅层网络【三五层那种】才用sigmoid 作为激活函数。
    2.其次，它能加快收敛速度。

---

目录

（1）sigmoid 函数 (以前最常用) 

（2）tanh  (双曲正切函数 ;Hyperbolic tangent function) 

  (3)  relu （Rectified linear unit; 修正线性单元 ）

（4）Leaky Relu  (带泄漏单元的relu )                     (5)  RReLU（随机ReLU）

（6）softsign                    （7）softplus                （8）Softmax   

（9）阈值函数 、阶梯函数                                    （10）分段线性函数 

---

 

（1）sigmoid 函数 (以前最常用) 

参数  α  > 0 可控制其斜率。 sigmoid 将一个实值输入压缩至[0,1]的范围,也可用于二分类的输出层。

---

（2）tanh  (双曲正切函数 ;Hyperbolic tangent function) 

 将 一个实值输入压缩至 [-1, 1]的范围，这类函数具有平滑和渐近性，并保持单调性.

---

(3)  relu （Rectified linear unit; 修正线性单元 ）

 深度学习目前最常用的激活函数

1.  
   # Relu在tensorflow中的实现： 直接调用函数
2.  
   tf.nn.relu( features, name= None )
3.  
        

与Sigmoid/tanh函数相比，ReLu激活函数的优点是：

•  使用梯度下降（GD）法时，收敛速度更快  
• 相比Relu只需要一个门限值，即可以得到激活值，计算速度更快  

 缺点是：  Relu的输入值为负的时候，输出始终为0，其一阶导数也始终为0，这样会导致神经元不能更新参数，也就是神经元不学习了，这种现象叫做“Dead Neuron”。

 为了解决Relu函数这个缺点，在Relu函数的负半区间引入一个泄露（Leaky）值，所以称为Leaky Relu函数。

---

 （4）Leaky Relu  (带泄漏单元的relu )

              数学表达式： y = max(0, x) + leak*min(0,x) 

与 ReLu 相比 ，leak 给所有负值赋予一个非零斜率，  leak是一个很小的常数  ，这样保留了一些负轴的值，使得负轴的信息不会全部丢失） 

leaky ReLU

 

1.  
   #leakyRelu在tennsorflow中的简单实现
2.  
   tf.maximum(leak * x, x),

       比较高效的写法为：

1.  
   import tensorflow as tf
2.  
   def LeakyReLU(x,leak=0.2,name="LeakyReLU"):
3.  
   with tf.variable_scope(name):
4.  
   f1 = 0.5*(1 + leak)
5.  
   f2 = 0.5*(1 - leak)
6.  
   return f1*x+f2*tf.abs(x)

---

(5)  RReLU（随机ReLU）

在训练时使用RReLU作为激活函数，则需要从均匀分布U(I,u)中随机抽取的一个数值  ，作为负值的斜率。

（6）softsign

数学表达式：

      ，导数：

---

（7）softplus

          Softplus函数是Logistic-Sigmoid函数原函数。  ,加了1是为了保证非负性。Softplus可以看作是强制非负校正函数max(0,x)平滑版本。红色的即为ReLU。

---

 

 （8）Softmax

  用于多分类神经网络输出

---

（11）GELU ：高斯误差线性单元

在这篇论文中，作者展示了几个使用GELU的神经网络优于使用ReLU作为激活的神经网络的实例。GELU也被用于BERT。

GELU、ReLU和LeakyReLU的函数

1.  
   def gelu(x):
2.  
   return 0.5 * x * (1 + math.tanh(math.sqrt(2 / math.pi) * (x + 0.044715 * math.pow(x, 3))))
3.  
   def relu(x):
4.  
   return max(x, 0)
5.  
   def lrelu(x):
6.  
   return max(0.01*x, x)

---

以下两个是以前使用的：

（9）阈值函数 、阶梯函数

相应的输出   为 

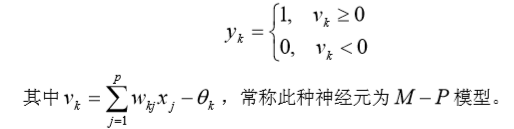
（10）分段线性函数 

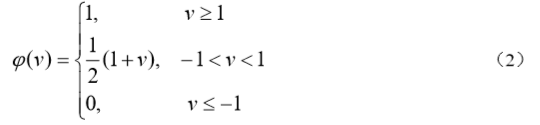
它类似于一个放大系数为 1 的非线性放大器，当工作于线性区时它是一个线性组合器， 放大系数趋于无穷大时变成一个阈值单元。 

 

3.Swish函数
Swish函数是一种自控门的激活函数，其定义：
Swish(x)=xσ(βx) Swish(x) = x\sigma(\beta x)
Swish(x)=xσ(βx)

其中，σ(⋅) \sigma(·)σ(⋅)函数是logistic函数，其值域在(−1,1) (-1,1)(−1,1)，β \betaβ是一个参数。也就是说当σ(⋅) \sigma(·)σ(⋅)趋近于1的时候，其输出和x xx本身近似；当σ(⋅) \sigma(·)σ(⋅)趋近于0的时候，其输出趋近于0。

3、基于Gate mechanism的GLU、GTU 单元

    介绍一下基于gate mechanism实现的，两个比较新颖的激活函数GTU和GLU。

    GTU（Gated Tanh Unit）的表达式为：

    f(X) = tanh(X*W+b) * O(X*V+c)

    GLU（Gated Liner Unit）的表达式为：

    f(X) = (X * W + b) * O(X * V + c)

    分析GTU和GLU的组成结构可以发现：

  Tanh激活单元：tanh(X*W+b)，加上一个Sigmoid激活单元：O(X*V+c)构成的gate unit，就构成了GTU单元。

   Relu激活单元：(X * W + b)，加上一个Sigmoid激活单元：O(X * V + c)构成的gate unit，就构成了GLU单元。

原文链接：https://blog.csdn.net/lqfarmer/article/details/72676715