浅谈人脸识别中的loss 损失函数

2019-04-17 17:57:33 liguiyuan112 阅读数 641更多

本文链接：https://blog.csdn.net/u012505617/article/details/89355690

在人脸识别中，算法的提高主要体现在损失函数的设计上，损失函数会对整个网络的优化有着导向性的作用。我们看到许多常用的损失函数，从传统的softmax loss到cosface, arcface 都有这一定的提高，这篇文章自己就来整理下这几个算法。

无论是SphereFace、CosineFace还是ArcFace的损失函数，都是基于Softmax loss来进行修改的。

Base line	Softmax loss
各种延伸的算法	Triplet loss, center loss
最新算法	A-Softmax Loss(SphereFace), Cosine Margin Loss, Angular Margin Loss, Arcface

1. Softmax loss

$\large L_1 = -\frac{1}{m}{\sum\limits_{i=1}^m}\log\left(\frac{e^{W^T_{y_i}x_i+b_{y_i}}}{ {\sum\limits_{j=1}^n}e^{W^T_jx_i+b_j} }\right)$

这就是softmax loss函数， ${W^T_{j}x_i+b_{j}}$ 表示全连接层的输出。在计算Loss下降的过程中，我们让 ${W^T_{j}x_i+b_{j}}$ 的比重变大，从而使得log() 括号内的数更变大来更接近1，就会 log(1) = 0，整个loss就会下降。

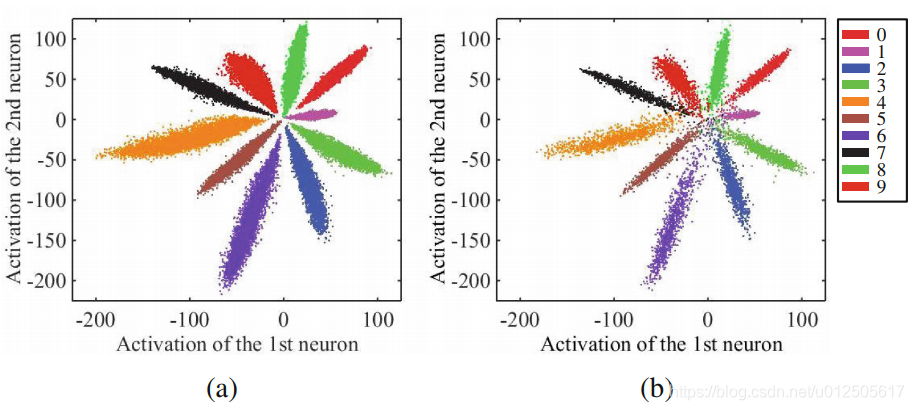
这种方式只考虑了能否正确分类，却没有考虑类间距离。所以提出了center loss 损失函数。(paper)

2. Center loss

$\large L_C = -\frac{1}{2}{\sum\limits_{i=1}^m}{||x_i-c_{y_i}||}^2$

$\large \Delta{c_j}=\frac{{\sum\limits_{i=1}^m}{\delta{(y_i=j)}\cdot{(c_j-x_i)}}}{1+{\sum\limits_{i=1}^m}{\delta{(y_i=j)}}}$

center loss 考虑到不仅仅是分类要对，而且要求类间有一定的距离。上面的公式中 $\large c_{y_i}$ 表示某一类的中心， $\large x_i$ 表示每个人脸的特征值。作者在softmax loss的基础上加入了 $\large L_C$ ，同时使用参数 $\large \lambda$ 来控制类内距离，整体的损失函数如下：

$\large L_2=L_S+L_C= -\frac{1}{m}{\sum\limits_{i=1}^m}\log\left(\frac{e^{W^T_{y_i}x_i+b_{y_i}}}{ {\sum\limits_{j=1}^n}e^{W^T_jx_i+b_j} }\right)+\frac{\lambda}{2}{\sum\limits_{i=1}^m}{||x_i-c_{y_i}||}^2$

3. Triplet Loss

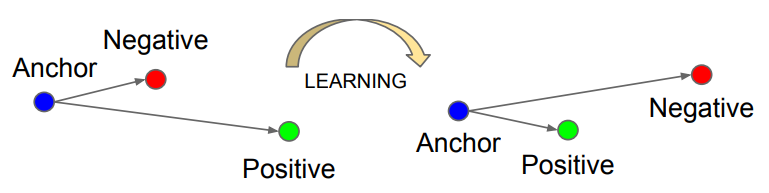
三元组损失函数，三元组由Anchor， Negative， Positive这三个组成。从上图可以看到，一开始Anchor离Positive比较远，我们想让Anchor和Positive尽量的靠近（同类距离），Anchor和Negative尽量的远离（类间距离）。

$\large L_3 = {\sum\limits_{i}^N}{\left [ ||f(x_i^a) - f(x_i^p)||^2_2 - ||f(x_i^a)-f(x_i^n)||_2^2 \right + \alpha ]}$

表达式左边为同类距离，右边为不同的类之间的距离。使用梯度下降法优化的过程就是让类内距离不断下降，类间距离不断提升，这样损失函数才能不断地缩小。

上面的几个算法都是比较传统老旧的，下面说一下比较新的算法。

4. L-softmax

前面Softmax loss函数没有考虑类间距离，Center loss函数可以使类内变得紧凑，但没有类间可分，而Triplet loss函数比较耗时，就产生了一下新的算法。

L-softmax函数开始就做了比较精细的改动，从softmax 函数log里面的 $\large e^{W^T_{y_i}x_i+b_{y_i}$ 转化到 $\large e^{||W_{yi}|| ||x_i||\psi{(\theta_{y_i})}}$ 。L-softmax函数不仅希望类间距离拉的更大，还能够把类内距离压缩的更紧凑。

$\LARGE L_4 = \frac{1}{N}\sum_{i=1}^N L_i = \frac{1}{N}\sum_{i=1}^N -log(\frac{e^{f_y_i}}{\sum_{j}e^{f_i}})$

$\LARGE L_i = -log(\frac{e^{||W_{yi}|| ||x_i||\psi{(\theta_{y_i})}}} {e^{||W_{yi}|| ||x_i||\psi{(\theta_{y_i})}} + \sum_{ j\neq y_i}{e^{||W_j|| ||x_i||cos(\theta_j)}}})$

把其中的cosθ改成了cos(mθ)，

$\large \psi(\theta) = \left\{\begin{matrix} \cos (m\theta ), 0\leqslant \theta \leqslant \frac{\pi }{m}& & \\ D(\theta), \frac{\pi}{m}\leqslant \theta \leqslant \pi & & \end{matrix}\right.$

m倍θ起到了增加 margin 的效果，让类内距离更加紧凑，同时类间距离变大。m越大类间距离就越大，因为在(0, π)区间cos函数单调递减，m越大 cos(mθ)趋向于0。

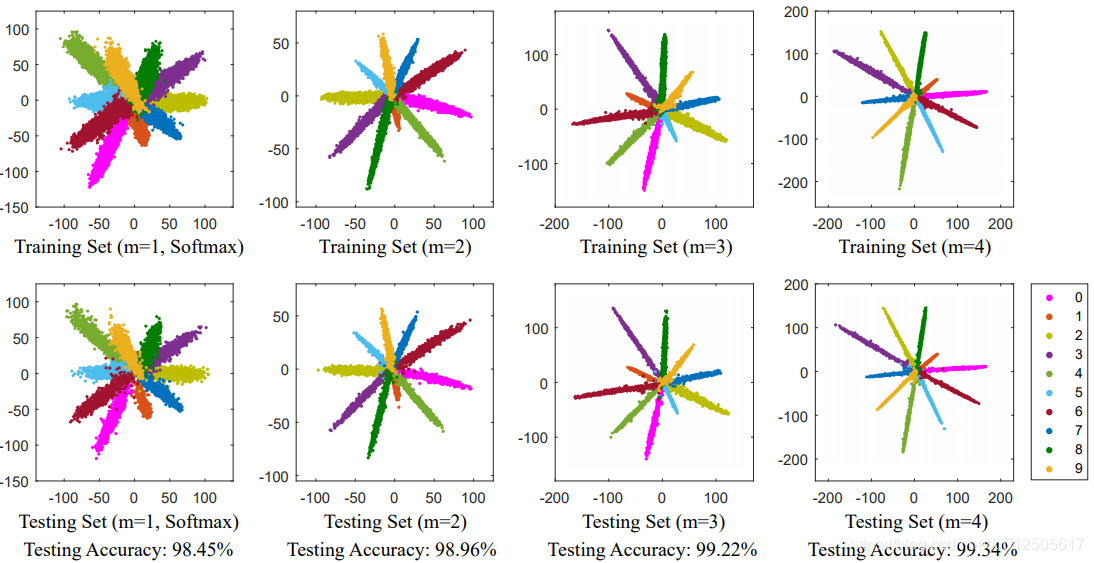
5. SphereFace(A-Softmax)

A-softmax 是在 L-softmax 函数上做了一个很小的修改，A-softmax 在考虑 margin时添加两个限制条件：将权重W归一化 $||W|| = 1$ ，b = 0。这使得模型的预测仅取决于 W 和 X 之间的角度。

$\LARGE L_5 = -\frac{1}{N}\sum_{i=1}^{N}log( \frac{e^{||x_i||\cos(m\theta_{y_i})}} {e^{||x_i||\cos(m\theta_{y_i})} + \sum_{j \neq y_i}{e^{||x_i||cos(\theta_j)}}})$

6. CosFace

cosface的loss函数如下：

$\LARGE L_6 = -\frac{1}{N} \sum_{i=1}^{N} log( \frac{e^{s(cos(\theta_{yi})-m)}}{e^{s(cos(\theta_{yi})-m)}+ \sum_{j=1, j\neq y_i}^k e^{scos \theta_j}})$

上式中，s为超球面的半径，m为margin。

7. ArcFace

对比arcface和cosface这两个函数，发现arcface是直接在角度空间中最大化分类界限，而cosface是在余弦空间中最大化分类界限，这样修改是因为角度距离比余弦距离在对角度的影响更加直接。

$\LARGE L_7= -\frac{1}{N} \sum_{i=1}^{N} log(\frac{e^{s(cos(\theta_{yi}+m))}}{e^{s(cos(\theta_{yi}+m))}+\sum_{j=1,j\neq y_i}^k e^{scos\theta_j}})$

分类的决策边界如下：

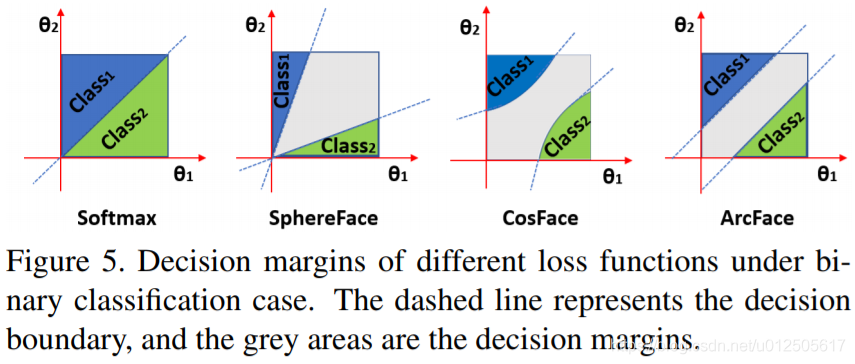
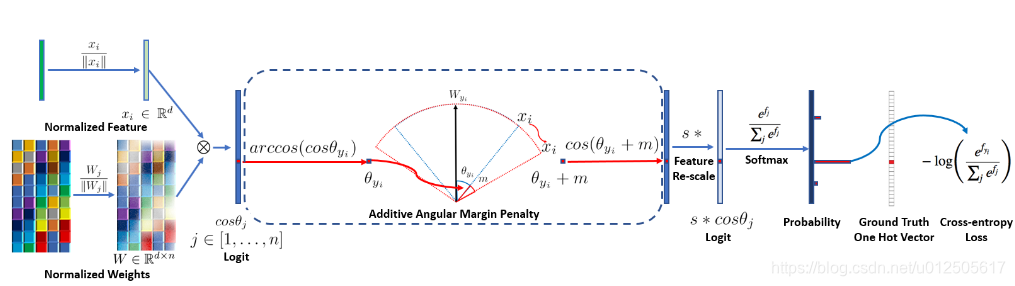
arcface算法流程如下：

posted on 2019-10-03 11:06 曹明阅读(4132) 评论(0) 编辑收藏举报