第七十四篇:机器学习优化方法及超参数设置综述
第七十四篇:机器学习优化方法及超参数设置综述
第七十四篇:机器学习优化方法及超参数设置综述
ps:很久没碰博客,长草了。。。应该坚持的。
摘 要
机器学习及其分支深度学习主要任务是模拟或者实现人类学习行为,这些学习方法近年来在目标分类、语音识别等各项任务中取得巨大突破。机器学的各种优化器极大了改善了学习模型的训练速度和泛化误差。优化方法和超参数作为观察训练模型的窗口,能够探索学习模型的结构和训练机制,是机器学习研究的重点之一。对机器学习的优化器与超参数理论研究进行了综述,回顾了超参数的一般搜索方法,对和优化器直接关联的批量大小、学习率超参数的设置方法进行了总结,对优化器和超参数需要进一步研究的问题进行了讨论。
关键词:机器学习;深度学习;梯度下降;优化器;超参数;学习率;批量大小;反向传播:
引言
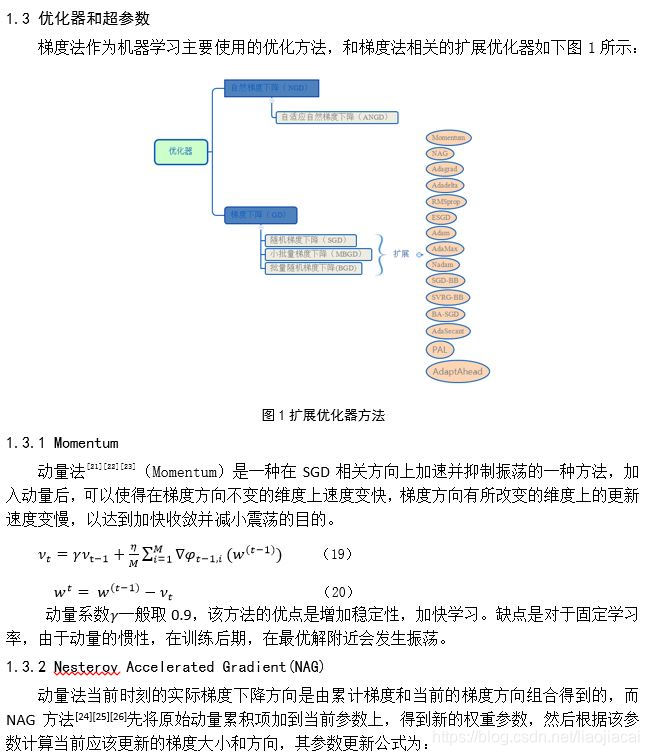
梯度下降法(GD)[1,2] 是解决无约束最优问题的一种方法,被广泛的使用在当前的机器学习[3,4]优化算法中。随着机器学习的发展,训练数据达到百万以上,如ImageNet[5],学习模型变得更深和更宽,训练时间长,收敛更慢,为了适应大数据和复杂模型的训练,解决这些训练问题,基于随机梯度下降扩展了各种优化器,并引入了更多的超参数,优化器的选择和超参数的设置影响网络的最终表现。深度学习的大多数模型可解释性较差,超参数及优化器可以作为一个观察、探索深度学习模型黑盒的一个工具,但是超参数设置仍然是当前机器学习训练的一个难题,手工调试超参数效率低下,近些年来提出了很多超参数的设置方法。本文从机器学习的问题、梯度下降和泛化误差的原理出发,分析梯度法与超参数的本质联系,并对基于理论产生的各种优化方法和超参数设置方法进行了总结。
机器学习优化算法:优化器及超参数
后记:很久没写博客了,CSDN用上了markdown,感觉还是不方便,截图挺好的。我传了这篇文档的pdf,大家可以下载看一下,欢迎大家指正错误,一起进步。下载地址:机器学习优化方法及超参数设置综述
参考文献
[1] ROBBINS, H MONRO S. A stochastic approximation method[J]. Statistics, 1951: 102–109.
[2] KALMAN R E. A New Approach to Linear Filtering and Prediction Problems[J]. Journal of Basic Engineering, 1960, 82(1): 35–45.
[3] LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. International Journal of Semantic Computing, 2016, 10(3): 417–439.
[4] JÜRGENSCHMIDHUBER. Deep Learning in Neural Networks : An Overview[J]. Neural Networks, 2014, 61: 85–117.
[5] DENG J, DONG W, RICHARD S et al. ImageNet : A Large-Scale Hierarchical Image Database[J]. 2009 IEEE Conference on Computer Vision and Pattern Recognition, IEEE, 2009: 248–255.
[6] QING A. An Introduction to Optimization[J]. Antennas & Propagation Magazine IEEE, 2013, 38(2): 60.
[7] YUAN Y. A Modified BFGS Algorithm for Unconstrained Optimization[J]. IMA Journal of Numerical Analysis, 1993, 11(3): 325–332.
[8] MOKHTARI A, RIBEIRO A. RES : Regularized Stochastic BFGS Algorithm[J]. IEEE Transactions on Signal Processing, 2014, 62(23): 6089–6104.
[9] ZHU C, H R, BYRD et al. Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization[J]. ACM Transactions on Mathematical Software, 1997, 23(4): 550–560.
[10] WILLIAMS D E R E H J. Learning internal representations by error propagation[M]. MIT Press Cambridge, MA, USA ©1988, 1988.
[11] HUTCHISON D, MITCHELL J C. Neural Networks: Tricks of the Trade[M]. 2012, 7700.
[12] J. DUCHI, E. HAZAN and Y S. Adaptive Subgradient Methods for Online Learningand Stochastic Optimization[J]. 2010: :2121–2159.
[13] GULCEHRE C, MOCZULSKI M, BENGIO Y. ADASECANT: Robust Adaptive Secant Method for Stochastic Gradient[J]. arXiv, 2014: arXiv:1412.7419.
[14] ITERATION S S. A GENERALIZATION OF THE HERMITIAN ANDSKEW-HERMITIAN SPLITTING ITERATION[J]. BIT Numerical Mathematics, 2003, 43(5): 881–900.
[15] SONG∗ S, CHAUDHURI† K, SARWATE‡ A D. Learning from Data with Heterogeneous Noise using SGD[J]. Journal of Machine Learning Research, 2015, 38: 1894–902.
[16] CHATURAPRUEK S, DUCHI J C, R´E C. Asynchronous stochastic convex optimization : the noise is in the noise and SGD don’t care[J]. Neural Information Processing Systems 2015, 2015.
[17] BOTTOU L, CURTIS F E, NOCEDAL J. Optimization Methods for Large-Scale Machine Learning[J]. SIAM Review, 2016, 60(2): 223–311.
[18] BOTTOU L´EON O B. The Tradeoffs of Large Scale Learning[J]. Advances in Neural Information Processing Systems 20, Proceedings of the Twenty-First Annual Conference on Neural Information Processing Systems, Vancouver, British Columbia, Canada, December 3-6, 2007. Curran Associates Inc. 2007., 2007: 161–168.
[19] PINHO M do R de, SHVARTSMAN I. Lipschitz continuity of optimal control and Lagrange multipliers in a problem with mixed and pure state constraints[J]. Discrete & Continuous Dynamical Systems - Series A (DCDS-A), 2012, 29(2): 505–522.
[20] WOOD G R, ZHANG B E. Estimation of the Lipschitz Constant of a Function[J]. Journal of Global Optimization, 1996, 8(1): 91–103.
[21] QIAN N. On the momentum term in gradient descent learning algorithms[J]. Neural Networks, 1999, 12(1): 145–151.
[22] POLYAK, JUDITSKY. Acceleration of Stochastic Approximation by Averaging[J]. SIAM Journal on Control and Optimization, 2014, 30(4): 838–855.
[23] YOSHUA B. Practical Recommendations for Gradient-Based Training of Deep Architectures[J]. arXiv, 2012: arXiv:1612.02803.
[24] NESTEROV Y. Convex Optimization[M]. Springer, Boston, MA, 2013.
[25] SU W, BOYD S, CANDES E J. A Differential Equation for Modeling Nesterov’s Accelerated Gradient Method: Theory and Insights[J]. Journal of Machine Learning Research, 2016, 17: 1–43.
[26] BUBECK S, LEE Y T, SINGH M. A geometric alternative to Nesterov’s accelerated gradient descent[J]. Mathematics, 2015: 1–9.
[27] DUCHI J, HAZAN E, YORAM SINGER et al. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization ∗[J]. 2011, 12: 2121–2159.
[28] JOHN C. ADADELTA: AN ADAPTIVE LEARNING RATE METHOD J. Mach. Learn. Res. 12 (2011), 2121 – 2159.[J]. 2011: 2009–2011.
[29] BECKER S, BOBIN J, BOBIN J. NESTA : A Fast and Accurate First-Order Method for Sparse Recovery ∗[J]. SIAM Journal on Imaging Sciences, 2011, 4(1): 1–39.
[30] DAUPHIN Y N, VRIES H De, BENGIO Y. Equilibrated adaptive learning rates for non-convex optimization[J]. NIPS’15 Proceedings of the 28th International Conference on Neural Information Processing Systems, 2015, 1: 1504–1512.
[31] KINGMA D P, BA J L. ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION[J]. ICLR, 2015: 1–15.
[32] REDDI S J, KALE S, KUMAR S. On the Convergence of Adam and Beyond[J]. arXiv, 2019: arXiv:1904.09237.
[33] DOZAT T. Incorporating Nesterov Momentum intoAdam[J]. - ICLR, 2016.
[34] FENG J, ZHANG H, ZHANG, TIEYAN et al. Adaptive Natural Gradient Algorithm for Blind Convolutive Source Separation[J]. International Symposium on Neural Networks: Advances in Neural Networks. Springer-Verlag, 2007: 715–720.
[35] AMARI S. Natural Gradient Works Efficiently in Learning[M]. Bradford Company Scituate, MA, USA ©1999, 1999.
[36] PASCANU R, BENGIO Y. Natural Gradient Revisited for deep networks[J]. Computer Science, 2014, 37(10–11): 1655–1658.
[37] DRIVALIARIS N A S J P D. Improved Jacobian Eigen-Analysis Scheme for Accelerating Learning in Feedforward Neural Networks[J]. Cognitive Computation, 2015, 7(1): 86–102.
[38] KARAKIDA R, OKADA M, AMARI S. Adaptive Natural Gradient Learning Algorithms for Unnormalized Statistical Models[J]. Artificial Neural Networks and Machine Learning – ICANN 2016, 2016, 1: 427–434.
[39] PARK H, AMARI S, FUKUMIZU K. Adaptive natural gradient learning algorithms for various stochastic models[J]. Neural Networks, 2000, 13(7): 755–764.
[40] ZHAO J, YU X. Neurocomputing Adaptive natural gradient learning algorithms for Mackey – Glass chaotic time prediction[J]. Neurocomputing, Elsevier, 2015, 157: 41–45.
[41] ZHANG Z, SUN H, PENG L. Natural gradient algorithm for stochastic distribution systems with output feedback ✩[J]. Differential Geometry and its Applications, Elsevier B.V., 2013, 31(5): 682–690.
[42] GUO W, WEI H, TIANHONG LIU et al. An Adaptive Natural Gradient Method with Adaptive Step Size in Multilayer Perceptrons[J]. 2017 Chinese Automation Congress (CAC), 2017: 1593–1597.
[43] MUTSCHLER M, ZELL A. PAL : A fast DNN optimization method based on curvature information[J]. arXiv, : arXiv:1903.11991.
[44] HOSEINI F, SHAHBAHRAMI A, BAYAT P. AdaptAhead Optimization Algorithm for Learning Deep CNN Applied to MRI Segmentation[J]. Journal of Digital Imaging, Journal of Digital Imaging, 2019, 32(1): 105–115.
[45] KESKAR N S, SOCHER R. Improving Generalization Performance by Switching from Adam to SGD[J]. arXiv, 2017: arXiv:1712.07628.
[46] R. S Y, ROSE D C, THOMAS P. KARNOWSKI et al. Optimizing deep learning hyper-parameters through an evolutionary algorithm[J]. MLHPC ’15 Proceedings of the Workshop on Machine Learning in High-Performance Computing Environments, 2015(August 2016): 1–5.
[47] TINCHCOMBE M. Multilayer Feedforward Networks are Universal Approximators[J]. Neural Networks, 1989, 2(5): 359–366.
[48] CHANDRA P, SINGH Y. An activation function adapting training algorithm for sigmoidal feedforward networks[J]. Neurocomputing, 2004, 61: 429–437.
[49] CHENEY M, BORDEN B, STATE C等. Regularization of Inverse Problems[M]. 2015.
[50] BREUEL T M. The Effects of Hyperparameters on SGD Training of Neural Networks[J]. Computer Science, 2015: 1–19.
[51] BENGIO Y. Continuous optimization of hyper-parameters[J]. Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks. IJCNN 2000, 2000, 1: 1305.
[52] SMITH S P. Differentiation of the Cholesky Algorithm[J]. Joumal of Computational and Graphical Statistics, 1995, 4(2): 134–147.
[53] Y L, LÉON B, ORR G B et al. Efficient BackProp[J]. Neural Networks: Tricks of the Trade, this book is an outgrowth of a 1996 NIPS workshop . Springer-Verlag, 1998: 9–50.
[54] BAO Y, LIU Z. A Fast Grid Search Method in Support Vector Regression Forecasting Time Series[M]. Intelligent Data Engineering and Automated Learning – IDEAL 2006, Springer Berlin Heidelberg, 2006.
[55] BERGSTRA J, BENGIO Y. Random Search for Hyper-Parameter Optimization James[J]. Journal of Machine Learning Research, 2012, 13(1): 281–305.
[56] BERGSTRA J, YAMINS D, COX D D. Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures[J]. Proceedings of the 30th International Conference on Machine Learning, 2013: 115–123.
[57] HUTTER F, HOOS H, LEYTON-BROWN K. Sequential Model-Based Optimization for General Algorithm Configuration Lecture Notes in Computer Science[J]. International Conference on Learning and Intelligent Optimization, 2011: 507–523.
[58] BERGSTRA J, BARDENET R, YOSHUA BENGIO et al. Algorithms for Hyper-Parameter Optimization Algorithms for Hyper-Parameter Optimization[J]. 25th Annual Conference on Neural Information Processing Systems (NIPS 2011), 2011(December): 2546–2554.
[59] LI L, JAMIESON K, GIULIA DESALVO et al. Hyperband: A Novel Bandit-Based Approach to Hyperparameter Optimization[J]. Journal of Machine Learning Research, 2016, 18: 1–52.
[60] LORENZO P R, NALEPA J, MICHAL KAWULOK et al. Particle swarm optimization for hyper-parameter selection in deep neural networks-p481-ribalta_lorenzo[J]. : 481–488.
[61] KOUTNÍK J, SCHMIDHUBER J, GOMEZ F. Evolving deep unsupervised convolutional networks for vision-based reinforcement learning[J]. GECCO ’14 Proceedings of the 2014 Annual Conference on Genetic and Evolutionary Computation, 2014: 541–548.
[62] KOUTNÍK J, SCHMIDHUBER J, GOMEZ F. Online evolution of deep convolutional network for vision-based reinforcement learning[J]. International Conference on Simulation of Adaptive Behavior, 2014: 260–269.
[63] VERBANCSICS P, HARGUESS J. Image classification using generative neuro evolution for deep learning[J]. 2015 IEEE Winter Conference on Applications of Computer Vision, WACV 2015, IEEE, 2015: 488–493.
[64] LEVY E, DAVID O E, NETANYAHU N S. Genetic algorithms and deep learning for automatic painter classification[J]. GECCO ’14 Proceedings of the 2014 Annual Conference on Genetic and Evolutionary Computation, 2014(Dl): 1143–1150.
[65] LANDER S, SHANG Y. EvoAE-A New Evolutionary Method for Training Autoencoders for Deep Learning Networks[J]. 2015 IEEE 39th Annual International Computers, Software & Applications Conference, IEEE, 2015, 2: 790–795.
[66] VERMA B, GHOSH R. Combination Strategies for Finding Optimal Neural Network Architecture and Weights[J]. Neural Information Processing: Research and Development, 2004: 294–319.
[67] VILALTA R, DRISSI Y. A Perspective View and Survey of Meta-Learning[J]. Artificial Intelligence Review, 2002, 18(2): 77–95.
[68] MOHAMED MAHER S S. SmartML : A Meta Learning-Based Framework for Automated Selection and Hyperparameter Tuning for Machine Learning Algorithms[J]. the 22nd International Conference on Extending Database Technology (EDBT), 2019: 554–557.
[69] WISTUBA M, SCHILLING N, SCHMIDT-THIEME L. Hyperparameter optimization machines[J]. Proceedings - 3rd IEEE International Conference on Data Science and Advanced Analytics, DSAA 2016, IEEE, 2016: 41–50.
[70] BARDENET R, BRENDEL M, BAL´AZS K´EGL et al. Collaborative hyperparameter tuning[J]. Applied Physics Express, 2011, 4(5): 199–207.
[71] ILIEVSKI I, AKHTAR T, JIASHI FENG et al. Efficient Hyperparameter Optimization of Deep Learning Algorithms Using Deterministic RBF Surrogates[J]. AAAI, 2016: 822–829.
[72] YOGATAMA D, MANN G. Efficient Transfer Learning Method for Automatic Hyperparameter Tuning[J]. Proceedings of the Seventeenth International Conference on Artificial Intelligence and Statistics, PMLR, 2014, 33: 1077–1085.
[73] SNOEK J, LAROCHELLE H, ADAMS R P. Practical Bayesian Optimization of Machine Learning Algorithms[J]. NIPS’12 Proceedings of the 25th International Conference on Neural Information Processing Systems, 2012, 2: 1–12.
[74] MUTNY M, KRAUSE A. Efficient High Dimensional Bayesian Optimization with Additivity and Quadrature Fourier Features[J]. 2018(NeurIPS): 9019–9030.
[75] CHRIS THORNTON, FRANK HUTTER , HOLGER H. HOOS K L-B. Auto-WEKA: Combined Selection and Hyperparameter Optimization of Classification Algorithms[J]. Proceedings of the 19th ACM SIGKDD international conference on Knowledge discovery and data mining, 2013: 847–855.
[76] AARON KLEIN S F, BARTELS, SIMON et al. Fast Bayesian Optimization of Machine Learning Hyperparameters on Large Datasets[J]. the 20th International Conference on Artificial In- telligence and Statistics (AISTATS) 2017, 2016, 54: 1–10.
[77] MURUGAN P. Hyperparameters Optimization in Deep Convolutional Neural Network / Bayesian Approach with Gaussian Process Prior[J]. arXiv, 2017: arXiv:1712.07233.
[78] KIM J, KIM S, CHOI S. Learning to Warm-Start Bayesian Hyperparameter Optimization[J]. NIPS, 2017: 1–14.
[79] HINTON G E. A Practical Guide to Training Restricted Boltzmann Machines[J]. Neural Networks: Tricks of the Trade, 2012: 599–619.
[80] CHENGWEI YAO D C, JIAJUN BU et al. Pre-training the deep generative models with adaptive hyperparameter optimization[J]. Neurocomputing, Elsevier B.V., 2017, 247: 144–155.
[81] BOYAN A, MOORE A W. Learning evaluation functions for global optimization and boolean satisfiability[J]. AAAI, 1998: 3–10.
[82] GAMBARDELLA L M, DORIGO M. Ant-Q: A Reinforcement Learning approach to the traveling salesman problem[J]. Machine Learning Proceedings 1995, 2014: 252–260.
[83] ENGINEERS E. Global Search in Combinatorial Optimization using Reinforcement Learning Algorithms Global Search in Combinatorial Optimization using Reinforcement Learning Algorithms[J]. Proceedings of the 1999 Congress on Evolutionary Computation-CEC99, 1999: 189–196.
[84] MOLL R, PERKINS T J, BARTO A G. Machine Learning for Subproblem Selection[J]. Proc. 17th International Conf. on Machine Learning, 2000: 615–622.
[85] HANSEN S. Using Deep Q-Learning to Control Optimization Hyperparameters[J]. arXiv, 2016: arXiv:1602.04062.
[86] POGGIO T. Regularization algorithms for learning that are equivalent to multilayer networks[J]. Science, 1990, 247(4945): 978–982.
[87] BROWN B M. Martingale Central Limit Theorems[J]. The Annals of Mathematical Statistics, 1971, 42(1): 59–66.
[88] BALLES L, ROMERO J, HENNIG P. Coupling Adaptive Batch Sizes with Learning Rates[J]. Association for Uncertainty in Artificial Intelligence, 2017: 410–419.
[89] KROGH* A, HERTZ J A. A Simple Weight Decay Can Improve Generalization[J]. NIPS’91 Proceedings of the 4th International Conference on Neural Information Processing Systems, 1991: 950–957.
[90] BYRD R H, CHIN G M, NOCEDAL, JORGE et al. Sample size selection in optimization methods for machine learning[J]. Mathematical Programming, 2012, 134(1): 127–155.
[91] MASTERS D, LUSCHI C. Revisiting Small Batch Training for Deep Neural Networks[J]. 2018: 1–18.
[92] PEDREGOSA F. Hyperparameter optimization with approximate gradient[J]. the 33rd International Conference on Machine Learning, 2016, 48: 737–746.
[93] LI M, ZHANG T, YUQIANG CHEN et al. Efficient mini-batch training for stochastic optimization[J]. Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining - KDD ’14, 2014: 661–670.
[94] AKIBA T, SUZUKI S, FUKUDA K. Extremely Large Minibatch SGD: Training ResNet-50 on ImageNet in 15 Minutes[J]. arXiv, 2017: arXiv:1711.04325.
[95] YOU Y, LI J, SASHANK REDDI et al. Large Batch Optimization for Deep Learning: Training BERT in 76 minutes[J]. arXiv, 2019: arXiv:1904.00962v3.
[96] YIN P, LUO P, NAKAMURA T. Small Batch or Large Batch? Gaussian Walk with Rebound Can Teach[J]. Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2017: 1275–1284.
[97] JADERBERG M, DALIBARD V, SIMON OSINDERO et al. Population Based Training of Neural Networks[J]. arXiv, 2017: arXiv:1711.09846.
[98] HAZAN E, KLIVANS A, YUAN Y. Hyperparameter Optimization: A Spectral Approach[J]. ICLR, 2018: 1–18.
[99] KESKAR N S, MUDIGERE D, NOCEDAL, JORGE et al. On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima[J]. ICLR, 2017.
[100] HOCHREITER S, SCHMIDHUBER J. FLAT MINIMA[J]. Neural Computation, 1997, 9(1): 1–42.
[101] DEVARAKONDA A, NAUMOV M, GARLAND M. AdaBatch: Adaptive Batch Sizes for Training Deep Neural Networks[J]. ARXIV, 2017: 1–14.
[102] YOU Y, GITMAN I, GINSBURG B. Scaling SGD Batch Size to 32K for ImageNet Training[J]. arXiv, 2017: arXiv:1708.03888v2.
[103] DE S, YADAV A, JACOBS D et al. Big Batch SGD: Automated Inference using Adaptive Batch Sizes[J]. International Conference on Artificial Intelligence and Statistics, 2016, 2017: 1–20.
[104] DE S, YADAV A, DAVID J et al. Automated Inference with Adaptive Batches[J]. Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, 2017, 54: 1504–1513.
[105] HOFFER E, HUBARA I, SOUDRY D. Train longer, generalize better: closing the generalization gap in large batch training of neural networks[J]. Advances in Neural Information Processing Systems, 2017: 1729–1739.
[106] SAMUEL L. SMITH∗ P-J K et al. Don’t Decay the Learning Rate, Increase the Batch Size[J]. ICLR, 2018.
[107] SMITH S L, LE Q V. A Bayesian Perspective on Generalization and Stochastic Gradient Descent[J]. ICLR, 2018.
[108] MANDIC D P, CHAMBERS J A. Towards the Optimal Learning Rate for Backpropagation[J]. Neural Processing Letters, 2000, 11(1): 1–5.
[109] XIAO-HU YU, GUO-AN CHEN, SHI-XIN CHENG. Dynamic learning rate optimization of the backpropagation algorithm[J]. IEEE Transactions on Neural Networks, 1995, 6(3): 669–677.
[110] SEONG S, LEE Y, YOUNGWOOK K et al. Towards Flatter Loss Surface via Nonmonotonic Learning Rate Scheduling[J]. In UAI2018 Conference on Uncertainty in Artificial Intelligence,Association for Uncertainty in Artificial Intelligence (AUAI), 2018.
[111] POLYAK B T. Some methods of speeding up the convergence of iteration methods[J]. USSR Computational Mathematics and Mathematical Physics, 1964, 4(5): 1–17.
[112] OBERMAN A M, PRAZERES M. Stochastic Gradient Descent with Polyak’s Learning Rate. (arXiv:1903.08688v1 [math.OC])[J]. arXiv Optimization and Control, 2019, 0167.
[113] JEFFREY DEAN, GREG S. CORRADO R M. Large Scale Distributed Deep Networks[J]. NIPS’12 Proceedings of the 25th International Conference on Neural Information Processing Systems, 2012, 1: 1223–1231.
[114] MARTENS J. Deep learning via Hessian-free optimization[J]. ICML’10 Proceedings of the 27th International Conference on International Conference on Machine Learning, 2010: 735–742.
[115] SCHAUL T, ZHANG S, LECUN Y. No More Pesky Learning Rates[J]. the 30th International Conference on International Conference on Machine Learning, 2013, 28: 343–351.
[116] RAVAUT M, GORTI S. Gradient descent revisited via an adaptive online learning rate[J]. arXiv, 2018: arXiv:1801.09136.
[117] BENGIO Y. Practical Recommendations for Gradient-Based Training of Deep Architectures BT - Neural Networks: Tricks of the Trade: Second Edition[M]. Springer, 2012.
[118] GEORGE A P, POWELL W B. Adaptive stepsizes for recursive estimation with applications in approximate dynamic programming[J]. Machine Learning, 2006, 65: 167–198.
[119] LUO H, HANAGUD S. Dynamic learning rate neural network training and delamination detection[J]. AIAA, 2013, 35(9): 1522–1527.
[120] SMITH L N. Cyclical learning rates for training neural networks[J]. Proceedings - 2017 IEEE Winter Conference on Applications of Computer Vision, WACV 2017, 2017, 1: 464–472.
[121] MISHRA S, YAMASAKI T, IMAIZUMI H. Improving image classifiers for small datasets by learning rate adaptations[J]. arXiv, 2019: arXiv:1903.10726.
[122] SCHAUL T, LECUN Y. Adaptive learning rates and parallelization for stochastic, sparse, non-smooth gradients[J]. arXiv, 2013: arXiv:1301.3764.
[123] TAKASE T, OYAMA S, KURIHARA M. Effective neural network training with adaptive learning rate based on training loss[J]. Neural Networks, Elsevier Ltd, 2018, 101: 68–78.
[124] YEDIDA R, SAHA S. A novel adaptive learning rate scheduler for deep neural networks[J]. arXiv, 2019: arXiv:1902.07399.
[125] SMITH L N. A disciplined approach to neural network hyper-parameters: Part 1 – learning rate, batch size, momentum, and weight decay[J]. arXiv, 2018: arXiv:1803.09820.
[126] LOSHCHILOV I, HUTTER F. SGDR: Stochastic Gradient Descent with Warm Restarts[J]. ICLR, 2017.
[127] WU X, WARD R, BOTTOU L. WNGrad: Learn the Learning Rate in Gradient Descent[J]. arXiv, 2018: arXiv:1803.02865.
[128] TAN† C, MA† S, AYU-HONG D et al. Barzilai-Borwein Step Size for Stochastic Gradient Descent[J]. the 30th International Conference on Neural Information Processing Systems, 2016: 685–693.
[129] CHANDRA B, SHARMA R K. Deep learning with adaptive learning rate using laplacian score[J]. Expert Systems with Applications, Elsevier Ltd, 2016, 63: 1–7.
[130] REN G, CAO Y, SHIPING W et al. A modified Elman neural network with a new learning rate scheme[J]. Neurocomputing, Elsevier B.V., 2018, 286: 11–18.
[131] HSIEH H L, SHANECHI M M. Optimizing the learning rate for adaptive estimation of neural encoding models[M]. PLoS Computational Biology, 2018, 14(5).


































 浙公网安备 33010602011771号
浙公网安备 33010602011771号