贝叶斯优化 Bayesian Optimization
贝叶斯优化 Bayesian Optimization
关键字:提取函数aquisition function,熵,响应曲面
简介:所谓优化,实际上就是一个求极值的过程,数据科学的很多时候就是求极值的问题。那么怎么求极值呢?很显然,很容易想到求导数,这是一个好方法,但是求导即基于梯度的优化的条件是函数形式已知才能求出导数,并且函数要是凸函数才可以。然而实际上很多时候是不满足这两个条件的,所以不能用梯度优化,贝叶斯优化应运而生了。
贝叶斯优化常原来解决反演问题,
(反演问题是指由结果及某些一般原理(或模型)出发去确定表征问题特征的参数(或模型参数))
贝叶斯优化的好处在于只需要不断取样,来推测函数的最大值。并且采样的点也不多。
一、贝叶斯优化的适用条件
不知道函数的具体形态即表达式
但是如果给定一个x,可以计算y。这里的计算方法可以使用之前的GPR,如果(x,y)够多了,那么就基本知道函数图像的走势了。
适用于小于20维的空间上优化
二、目的
找出函数的最值,这是最主要的目的。因为很多时候数据科学的一大部分问题都是做非线性函数f(x)的在范围A内的优化,或者简 单的说,求最大值/最小值。比如需要确定拟合的参数,可以求出关于参数的代价函数,求得该代价函数的最小值就可以确定 对应的最优参数了。那么求这个最小值就需要贝叶斯优化了。
大致知道函数长什么样子:与响应曲面相比,贝叶斯只知道最后函数大概什么走向,但是不知道自变量与因变量的关系。可以大致理解为构建响应曲面(虽然响应曲面努力拟合自变量与因变量的关系,下面是关于响应曲面)
响应曲面设计是利用合理的试验设计方法并通过实验得到一定数据,采用多元二次回归方程来拟合与响应值之间的函数关系,通过对回归方程的分析来寻求最优工艺参数,解决多变量问题的一种统计方法。
将响应看作是因素的函数,使用图形技术体现这种函数。一般假设指标和因素之间的关系可以用线性模型表示,即使用多元线性回归的方法。考虑m个因素和n个结果之间的关系,经常使用最小二乘法(就是我们数学上的曲线拟合。注意网页的线性最小二乘法的那一项,很重要。)
对于超定方程组,引入残差平方和函数,最优解为
三、思路
1.因为GP可以得到在一个新的点x的后验概率P(f(x)|x,D),这里的D为数据集,所以如果想求得极值,可以从GP计算出的x点的均值和方差考虑。可以根据该后验概率的一些指标确定下一个我应该取哪一个点,才有较大的概率尽快的达到极值。
2.如何选取下一个点:求提取函数u达到极值对应的x。这就是上一条的所谓指标。
3.基本算法
可以看出,这里就是不断的求max(AF)对应的点Xt,计算Xt的Yt,即取样,加到数据集。周而复始的循环。
原谅我写的X,Y都是大写,否则x和t一样大了,强迫症发作
关于D,D中的数据周围的方差都较小,也就是我们对他们周围的点了解较多,所以只要有足够多的数据到D里面,那么就会收敛到f(x)
4.Xt的选取
是x点的均值,
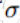
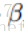
5.优化方向
explore 探索未知的空间,尽可能的探索未知的空间,这样对f(x)的后验概率才会更接近f(x)
exploit,强化已有的结果,在现有最大值的附近进行探索,保证找到的f(x)会更大
6.常用的AF
6.1 probability of improvement(POI)
目的:新的采样能提升最大值的概率最大
表达式为:MPI(maximum probability of improvement),或P算法
Φ(·) 表示的是正态累计分布函数
改进:这里的参数为trade-off系数,可以控制倾向explore还是exploit
这里倾向于局部搜索
6.2 Expected improvement(EI)
可以在explore和explot之间平衡,explore时选择均值大的点,exploit选择方差大的点
参数通常选0.01
6.3 Upper confidence bound
直接比较置信区间的最大值,效果非常好
参考:http://blog.sina.com.cn/s/blog_76d02ce90102xqs6.html




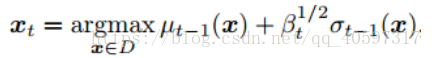
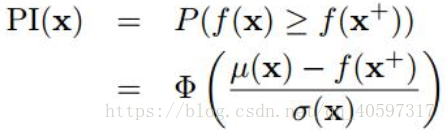
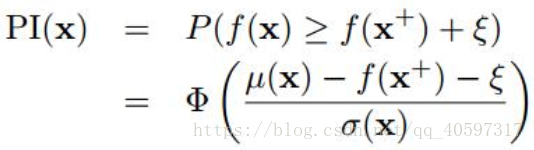
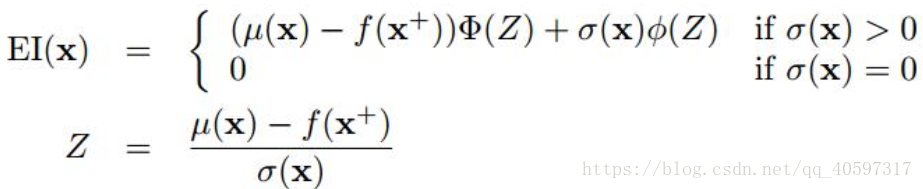
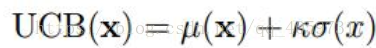

 浙公网安备 33010602011771号
浙公网安备 33010602011771号