FLeiss Kappa系数和Kappa系数的Python实现
FLeiss Kappa系数和Kappa系数的Python实现
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
Kappa系数和Fleiss Kappa系数是检验实验标注结果数据一致性比较重要的两个参数,其中Kappa系数一般用于两份标注结果之间的比较,Fleiss Kappa则可以用于多份标注结果的一致性检测,我在百度上面基本上没有找到关于Fleiss Kappa系数的介绍,于是自己参照维基百科写了一个模板出来,参考的网址在这里:维基百科-Kappa系数
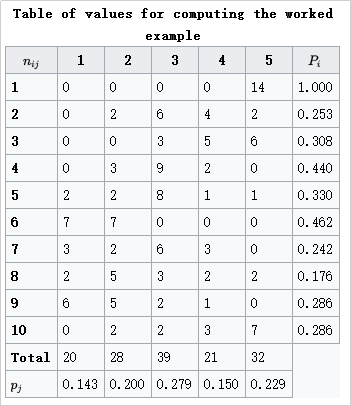
这里简单介绍一下Fleiss Kappa系数的计算过程,假设有以下数据:
以上是14个人对于10个任务进行的5级标注的结果(N = 10,n = 14, k = 5),以上计算Fleiss Kappa系数的过程如下:
①对于Pj的计算,为每一列结果相乘除以任务总数,这里任务总数为14*10=140,对应于Kappa系数中每个分类的随机一致概率,然后由于Fleiss Kappa没有一个参照的标注值,因此这里计算Pe理论一致性的时候,将每个Pj进行平方求和,例如求Pj=1的计算情况如下:
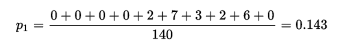
②而对于Pi的计算,是对每一个标注任务进行实际一致性的计算,也就是要计算:在所有的排列中(这里用组合也可以,但是包含顺序比较方便计算),具有一致性的排列有多少个,所以分母就是全排列的个数n*(n-1),而分子是这一行所有数平方和减去n(标注人数),表示实际上一致的标注对数(pairs)。为什么要减去n?因为直接各项平方相加包含了这n个标注人员自己和自己标注结果组成的pair,这样会有重复,所以要减去n。因此,Pi=2的计算情况如下:
③最后计算Fleiss Kappa系数,有:
这里附上实现相应的python代码:
-
# -*- encoding: utf-8 -*-
-
-
# 2017-7-27 by xuanyuan14
-
# 求Kappa系数和Fleiss Kappa系数的模板
-
# 分集0.0~0.20极低的一致性(slight)、0.21~0.40一般的一致性(fair)、0.41~0.60 中等的一致性(moderate)
-
# 0.61~0.80 高度的一致性(substantial)和0.81~1几乎完全一致(almost perfect)
-
-
import numpy as np
-
-
def kappa(testData, k): #testData表示要计算的数据,k表示数据矩阵的是k*k的
-
dataMat = np.mat(testData)
-
P0 = 0.0
-
for i in range(k):
-
P0 += dataMat[i, i]*1.0
-
xsum = np.sum(dataMat, axis=1)
-
ysum = np.sum(dataMat, axis=0)
-
#xsum是个k行1列的向量,ysum是个1行k列的向量
-
Pe = float(ysum*xsum)/k**2
-
P0 = float(P0/k*1.0)
-
cohens_coefficient = float((P0-Pe)/(1-Pe))
-
return cohens_coefficient
-
-
def fleiss_kappa(testData, N, k, n): #testData表示要计算的数据,(N,k)表示矩阵的形状,说明数据是N行j列的,一共有n个标注人员
-
dataMat = np.mat(testData, float)
-
oneMat = np.ones((k, 1))
-
sum = 0.0
-
P0 = 0.0
-
for i in range(N):
-
temp = 0.0
-
for j in range(k):
-
sum += dataMat[i, j]
-
temp += 1.0*dataMat[i, j]**2
-
temp -= n
-
temp /= (n-1)*n
-
P0 += temp
-
P0 = 1.0*P0/N
-
ysum = np.sum(dataMat, axis=0)
-
for i in range(k):
-
ysum[0, i] = (ysum[0, i]/sum)**2
-
Pe = ysum*oneMat*1.0
-
ans = (P0-Pe)/(1-Pe)
-
return ans[0, 0]
-
-
-
if __name__ == "__main__":
-
dataArr1 = [[1.1, 1.2], [3.23, 4.78]]
-
dataArr2 = [[0, 0, 0, 0, 14],
-
[0, 2, 6, 4, 2],
-
[0, 0, 3, 5, 6],
-
[0, 3, 9, 2, 0],
-
[2, 2, 8, 1, 1],
-
[7, 7, 0, 0, 0],
-
[3, 2, 6, 3, 0],
-
[2, 5, 3, 2, 2],
-
[6, 5, 2, 1, 0],
-
[0, 2, 2, 3, 7]]
-
res1 = kappa(dataArr1, 2)
-
res2 = fleiss_kappa(dataArr2, 10, 5, 14)
-
print res1, res2
-
-
#>>>0.855919552608 0.209930704422
-



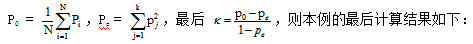
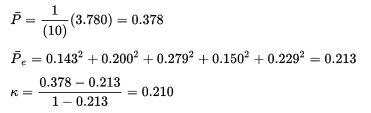

 浙公网安备 33010602011771号
浙公网安备 33010602011771号