预测评价指标RMSE、MSE、MAE、MAPE、SMAPE
预测评价指标RMSE、MSE、MAE、MAPE、SMAPE
假设:
预测值:yˆ={y1ˆ,y2ˆ,...,ynˆ}\mathbf{\hat{y}}=\{\hat{y_1}, \hat{y_2} , ... , \hat{y_n}\}y^={y1^,y2^,...,yn^}
真实值:y={y1,y2,...,yn}\mathbf{y}=\{y_1, y_2, ..., y_n\}y={y1,y2,...,yn}
MSE
均方误差(Mean Square Error)
MSE=1n∑ni=1(yˆi−yi)2MSE=\frac{1}{n} \sum_{i=1}^{n} (\hat{y}_i - y_i)^2MSE=n1i=1∑n(y^i−yi)2
范围[0,+∞),当预测值与真实值完全吻合时等于0,即完美模型;误差越大,该值越大。
RMSE
均方根误差(Root Mean Square Error),其实就是MSE加了个根号,这样数量级上比较直观,比如RMSE=10,可以认为回归效果相比真实值平均相差10。
RMSE=1n∑ni=1(yˆi−yi)2−−−−−−−−−−−−−−√RMSE=\sqrt{\frac{1}{n} \sum_{i=1}^{n} (\hat{y}_i - y_i)^2}RMSE=n1i=1∑n(y^i−yi)2
MAE
平均绝对误差(Mean Absolute Error)
MAE=1n∑ni=1∣yˆi−yi∣MAE=\frac{1}{n} \sum_{i=1}^{n} |\hat{y}_i - y_i|MAE=n1i=1∑n∣y^i−yi∣
范围[0,+∞),当预测值与真实值完全吻合时等于0,即完美模型;误差越大,该值越大。
MAPE
平均绝对百分比误差(Mean Absolute Percentage Error)
MAPE=100%n∑ni=1∣∣yˆi−yiyi∣∣MAPE=\frac{100\%}{n}\sum_{i=1}^n \left |\frac{ \hat{y}_i - y_i }{ y_i } \right |MAPE=n100%i=1∑n∣∣∣∣yiy^i−yi∣∣∣∣
范围[0,+∞),MAPE 为0%表示完美模型,MAPE 大于 100 %则表示劣质模型。
可以看到,MAPE跟MAE很像,就是多了个分母。
注意点:当真实值有数据等于0时,存在分母0除问题,该公式不可用!
SMAPE
对称平均绝对百分比误差(Symmetric Mean Absolute Percentage Error)
SMAPE=100%n∑ni=1∣yˆi−yi∣(∣yˆi∣+∣yi∣)/2SMAPE=\frac{100\%}{n}\sum_{i=1}^n \frac{ |\hat{y}_i - y_i| }{ (|\hat{y}_i| + |y_i|)/2 }SMAPE=n100%i=1∑n(∣y^i∣+∣yi∣)/2∣y^i−yi∣
注意点:当真实值有数据等于0,而预测值也等于0时,存在分母0除问题,该公式不可用!
Python代码
# coding=utf-8
import numpy as np
from sklearn import metrics
# MAPE和SMAPE需要自己实现
def mape(y_true, y_pred):
return np.mean(np.abs((y_pred - y_true) / y_true)) * 100
def smape(y_true, y_pred):
return 2.0 * np.mean(np.abs(y_pred - y_true) / (np.abs(y_pred) + np.abs(y_true))) * 100
y_true = np.array([1.0, 5.0, 4.0, 3.0, 2.0, 5.0, -3.0])
y_pred = np.array([1.0, 4.5, 3.5, 5.0, 8.0, 4.5, 1.0])
# MSE
print(metrics.mean_squared_error(y_true, y_pred)) # 8.107142857142858
# RMSE
print(np.sqrt(metrics.mean_squared_error(y_true, y_pred))) # 2.847304489713536
# MAE
print(metrics.mean_absolute_error(y_true, y_pred)) # 1.9285714285714286
# MAPE
print(mape(y_true, y_pred)) # 76.07142857142858
# SMAPE
print(smape(y_true, y_pred)) # 57.76942355889724
MAPE 平均绝对百分误差
from fbprophet.diagnostics import performance_metrics
df_p = performance_metrics(df_cv)
df_p.head()
| horizon | mse | rmse | mae | mape | coverage | |
|---|---|---|---|---|---|---|
| 3297 | 37 days | 0.481970 | 0.694241 | 0.502930 | 0.058371 | 0.673367 |
| 35 | 37 days | 0.480991 | 0.693535 | 0.502007 | 0.058262 | 0.675879 |
| 2207 | 37 days | 0.480936 | 0.693496 | 0.501928 | 0.058257 | 0.675879 |
| 2934 | 37 days | 0.481455 | 0.693870 | 0.502999 | 0.058393 | 0.675879 |
| 393 | 37 days | 0.483990 | 0.695694 | 0.503418 | 0.058494 | 0.675879 |
mape平均绝对百分误差
-
- 定义
- 定义
-
def evalmape(preds, dtrain):
-
gaps = dtrain.get_label()
-
err = abs(gaps-preds)/gaps
-
err[(gaps==0)] = 0
-
err = np.mean(err)*100
-
return 'error',err
-
回归评价指标:MSE、RMSE、MAE、R2、Adjusted R2
1、均方误差:MSE(Mean Squared Error)
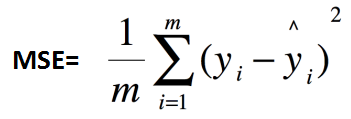
其中,![]() 为测试集上真实值-预测值。
为测试集上真实值-预测值。
2、均方根误差:RMSE(Root Mean Squard Error)
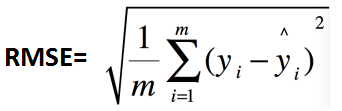
可以看出,RMSE=sqrt(MSE)。
3、平均绝对误差:MAE(Mean Absolute Error)
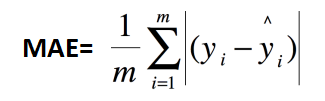
以上各指标,根据不同业务,会有不同的值大小,不具有可读性,因此还可以使用以下方式进行评测。
4、决定系数:R2(R-Square)
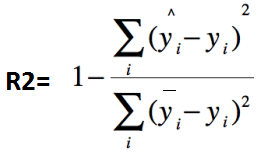
其中,分子部分表示真实值与预测值的平方差之和,类似于均方差 MSE;分母部分表示真实值与均值的平方差之和,类似于方差 Var。
根据 R-Squared 的取值,来判断模型的好坏,其取值范围为[0,1]:
如果结果是 0,说明模型拟合效果很差;
如果结果是 1,说明模型无错误。
一般来说,R-Squared 越大,表示模型拟合效果越好。R-Squared 反映的是大概有多准,因为,随着样本数量的增加,R-Square必然增加,无法真正定量说明准确程度,只能大概定量。
5、校正决定系数(Adjusted R-Square)
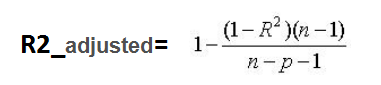
其中,n 是样本数量,p 是特征数量。
Adjusted R-Square 抵消样本数量对 R-Square的影响,做到了真正的 0~1,越大越好。
python中可以直接调用
-
from sklearn.metrics import mean_squared_error #均方误差
-
from sklearn.metrics import mean_absolute_error #平方绝对误差
-
from sklearn.metrics import r2_score#R square
-
#调用
-
MSE:mean_squared_error(y_test,y_predict)
-
RMSE:np.sqrt(mean_squared_error(y_test,y_predict))
-
MAE:mean_absolute_error(y_test,y_predict)
-
R2:r2_score(y_test,y_predict)
-
Adjusted_R2::1-((1-r2_score(y_test,y_predict))*(n-1))/(n-p-1)
- 1



 浙公网安备 33010602011771号
浙公网安备 33010602011771号