beta分布


beta分布介绍

相信大家学过统计学的都对 正态分布 二项分布 均匀分布 等等很熟悉了，但是却鲜少有人去介绍beta分布的。

用一句话来说，beta分布可以看作一个概率的概率分布，当你不知道一个东西的具体概率是多少时，它可以给出了所有概率出现的可能性大小。

举一个简单的例子，熟悉棒球运动的都知道有一个指标就是棒球击球率(batting average)，就是用一个运动员击中的球数除以击球的总数，我们一般认为0.266是正常水平的击球率，而如果击球率高达0.3就被认为是非常优秀的。

现在有一个棒球运动员，我们希望能够预测他在这一赛季中的棒球击球率是多少。你可能就会直接计算棒球击球率，用击中的数除以击球数，但是如果这个棒球运动员只打了一次，而且还命中了，那么他就击球率就是100%了，这显然是不合理的，因为根据棒球的历史信息，我们知道这个击球率应该是0.215到0.36之间才对啊。

对于这个问题，我们可以用一个二项分布表示（一系列成功或失败），一个最好的方法来表示这些经验（在统计中称为先验信息）就是用beta分布，这表示在我们没有看到这个运动员打球之前，我们就有了一个大概的范围。beta分布的定义域是(0,1)这就跟概率的范围是一样的。

接下来我们将这些先验信息转换为beta分布的参数，我们知道一个击球率应该是平均0.27左右，而他的范围是0.21到0.35，那么根据这个信息，我们可以取α=81,β=219


之所以取这两个参数是因为：

  • beta分布的均值是\frac{\alpha}{\alpha+\beta}=\frac{81}{81+219}=0.27
  • 从图中可以看到这个分布主要落在了(0.2,0.35)间，这是从经验中得出的合理的范围。

在这个例子里，我们的x轴就表示各个击球率的取值，x对应的y值就是这个击球率所对应的概率。也就是说beta分布可以看作一个概率的概率分布。

那么有了先验信息后，现在我们考虑一个运动员只打一次球，那么他现在的数据就是”1中;1击”。这时候我们就可以更新我们的分布了，让这个曲线做一些移动去适应我们的新信息。beta分布在数学上就给我们提供了这一性质，他与二项分布是共轭先验的（Conjugate_prior）。所谓共轭先验就是先验分布是beta分布，而后验分布同样是beta分布。结果很简单：


\mbox{Beta}(\alpha_0+\mbox{hits}, \beta_0+\mbox{misses})

其中α0和β0是一开始的参数，在这里是81和219。所以在这一例子里，α增加了1(击中了一次)。β没有增加(没有漏球)。这就是我们的新的beta分布Beta(81+1,219)，我们跟原来的比较一下：


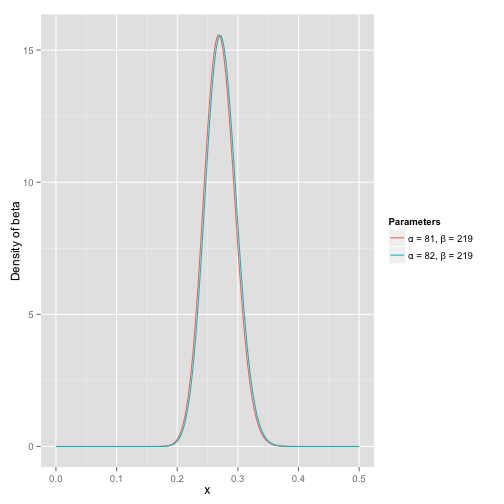
可以看到这个分布其实没多大变化，这是因为只打了1次球并不能说明什么问题。但是如果我们得到了更多的数据，假设一共打了300次，其中击中了100次，200次没击中，那么这一新分布就是：


\mbox{beta}(81+100, 219+200)

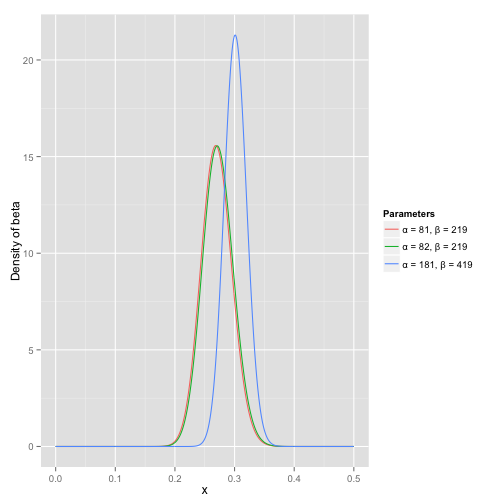
注意到这个曲线变得更加尖，并且平移到了一个右边的位置，表示比平均水平要高。

一个有趣的事情是，根据这个新的beta分布，我们可以得出他的数学期望为：\frac{\alpha}{\alpha+\beta}=\frac{82+100}{82+100+219+200}=.303，这一结果要比直接的估计要小 \frac{100}{100+200}=.333 。你可能已经意识到，我们事实上就是在这个运动员在击球之前可以理解为他已经成功了81次，失败了219次这样一个先验信息。

因此，对于一个我们不知道概率是什么，而又有一些合理的猜测时，beta分布能很好的作为一个表示概率的概率分布。

beta分布与二项分布的共轭先验性质二项分布

二项分布即重复n次独立的伯努利试验。在每次试验中只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，与其它各次试验结果无关，事件发生与否的概率在每一次独立试验中都保持不变，则这一系列试验总称为n重伯努利实验，当试验次数为1时，二项分布服从0-1分布

二项分布的似然函数：


P(data|\theta) \propto \theta^z(1-\theta)^{N-z} \\ z=\sum_{i=1}^NX_i
beta分布
Beta(a,b)=\frac{\theta^{a-1}(1-\theta)^{b-1}}{B(a,b)}\propto \theta^{a-1}(1-\theta)^{b-1}


在beta分布中，B函数是一个标准化函数，它只是为了使得这个分布的概率密度积分等于1才加上的。

贝叶斯估计

我们做贝叶斯估计的目的就是要在给定数据的情况下求出θ的值，所以我们的目的是求解如下后验概率：


P(\theta |data)=\frac{P(data|\theta)P(\theta)}{P(data)}\propto P(data|\theta)P(\theta)


注意到因为P(data)与我们所需要估计的θ是独立的，因此我们可以不考虑它。

我们称P(data|θ)为似然函数，P(θ)为先验分布

共轭先验

现在我们有了二项分布的似然函数和beta分布，现在我们将beta分布代进贝叶斯估计中的P(θ)中，将二项分布的似然函数代入P(data|θ)中，可以得到：


P(\theta |data) \propto \theta^z(1-\theta)^{N-z}*\theta^{a-1}(1-\theta)^{b-1} \\ \propto \theta^{a+z-1}(1-\theta)^{b+N-z-1}


我们设a′=a+z,b′=b+N−z
最后我们发现这个贝叶斯估计服从Beta(a’,b’)分布的，我们只要用B函数将它标准化就得到我们的后验概率：


P(\theta |data)=\frac{\theta^{a'-1}(1-\theta)^{b'-1}}{B(a',b')}
参考资料：

1.Understanding the beta distribution (using baseball statistics)
2.20 - Beta conjugate prior to Binomial and Bernoulli likelihoods


作为分享主义者(sharism)，本人所有互联网发布的图文均遵从CC版权，转载请保留作者信息并注明作者a358463121专栏:a358463121的专栏，如果涉及源代码请注明GitHub地址：358463121 (QJ) · GitHub。商业使用请联系作者。
参考原文：

Beta Distribution

Beta Distribution Definition:

 

f(x; a,b) = \frac{1}{B(\alpha, \beta)} x^{\alpha - 1}(1 - x)^{\beta - 1},

这里，因为Beta分数是二项分布的参数p的概率分布, 所以x（即p）的取值范围为0 <= x <= 1

where the normalisation, B, is thebeta function, Beta function could also be expressed by Gamma function:

Gamma函数 在实数域可以表示为：

Gamma函数 在整数域可以表示为：

Γ(n)=(n−1)!

Gamma函数有以下性质：

因为Beta函数可以表示为Gamma函数，所以Beta分布还可以表示为：

0 <= x <= 1

Beta分布可以理解为二项分布的参数p的分布，所以，这里重新定义Beta分布：

Beta分布的期望：

 

Beta分布的方差：

 

Beta分布的 众数 mode:


 

Beta分布的偏度 Skewness：


 

Beta分布的 峰度 Kurtosis:


 

Beta Distribution Examples

Beta分布可以说是一个百变星君，根据参数a,b的不同，可以呈现出多种完全不同的概率分布图.

生成Beta分布的代码：

 

[python] view plain copy
 
 在CODE上查看代码片派生到我的代码片
  1. from scipy.stats import beta  
  2. import matplotlib.pyplot as plt  
  3. import numpy as np  
  4.   
  5. a, b = 2, 1  
  6.   
  7. mean, var, skew, kurt = beta.stats(a, b, moments='mvsk')  
  8.   
  9. x = np.linspace(0, 1, 100)  
  10. plt.plot(x, beta.pdf(x, a, b), 'r-', lw=5, alpha=0.6, label='beta pdf')  
  11. plt.show()  

 

然后，根据调整代码中的a,b的取值，可以得到不同的Beta分布：

a, b = 2, 1:

a, b = 2, 2

a, b = 8, 2

a, b = 0.01, 20

a, b = 1, 1

这样一个一个的绘制，是不是太逊了， 画在一起：

代码：

 

[python] view plain copy
 
 在CODE上查看代码片派生到我的代码片
  1. from scipy.stats import beta  
  2. import matplotlib.pyplot as plt  
  3. import numpy as np  
  4.   
  5. x = np.linspace(0, 1, 100)  
  6.   
  7. a_array = [1, 2, 4, 8]  
  8. b_array = [1, 2, 4, 8]  
  9.   
  10. fig, axarr = plt.subplots(len(a_array), len(b_array))  
  11.   
  12. for i, a in enumerate(a_array):  
  13.   for j, b in enumerate(b_array):  
  14.     axarr[i, j].plot(x, beta.pdf(x, a, b), 'r', lw=1, alpha=0.6, label='a='+str(a)+',b='+str(b))  
  15.     axarr[i, j].legend(frameon=False)  
  16.   
  17. plt.show()  

 

将所有的Beta分布绘制在一个图上：

代码：

 

[python] view plain copy
 
 在CODE上查看代码片派生到我的代码片
  1. from scipy.stats import beta  
  2. import matplotlib.pyplot as plt  
  3. import numpy as np  
  4.   
  5. x = np.linspace(0, 1, 100)  
  6.   
  7. a_array = [1, 2, 4, 8]  
  8. b_array = [1, 2, 4, 8]  
  9.   
  10. for i, a in enumerate(a_array):  
  11.   for j, b in enumerate(b_array):  
  12.     plt.plot(x, beta.pdf(x, a, b), lw=1, alpha=0.6, label='a='+str(a)+',b='+str(b))  
  13.   
  14. plt.legend(frameon=False)  
  15. plt.show()  

 

Beta Mean

由公式可以得到，Beta分布的均值，也可以通过采样的方法，在一个Beta分布中，采样，计算均值。

代码：

 

[python] view plain copy
 
 在CODE上查看代码片派生到我的代码片
  1. import numpy as np  
  2. import numpy.random as nprnd  
  3. import scipy.stats as spstat  
  4. import scipy.special as ssp  
  5. import itertools as itt  
  6.   
  7. import matplotlib.pyplot as plt  
  8. import pylab as pl  
  9.   
  10. N = (np.arange(200) + 3) ** 2 * 20  
  11.   
  12. betamean = np.zeros_like(N, dtype=np.float64)  
  13.   
  14. for idx, i in enumerate(N):  
  15.     betamean[idx] = np.mean(nprnd.beta(2, 1, i))  
  16.   
  17. plt.plot(N, betamean, color='steelblue', lw=2)  
  18. plt.xscale('log')  
  19. plt.show()  
  20.   
  21. print spstat.beta(2, 1).mean()  
  22.   
  23. print spstat.beta(2, 1).mean(), 2.0 / (2 + 1)  
  24. print spstat.beta(2, 1).var(), 2 * 1.0 / (2 + 1 + 1) / (2 + 1) ** 2  

 

运行结果：

这里可以看到，随着采样点的增加，样本点的均值也就更加的收敛，更加的接近⅔,  ⅔ 是一个通过公式计算得到的。 这样，这个图片的结果也符合大数定理，随着采样点的增加，只要样本点无限大，那么最终的均值就会无限的接近⅔.

Conjugate Prior

A conjugate prior,p(p), of a likelihood, p(x|p), is a distribution that results in a posterior distribution, p(p|x)with the same functional form as the prior and a parameterisation that incorporates the observationx.

这句话，猛的一读，晕头转向，但是，仔细读上三五遍，基本上就理解了什么叫“共轭先验”。

基本上说，一个参数的共轭先验p(p)是这样的一个分布：在这个分布的基础上加上观测样本能够得到一个与先验分布具有相同的函数形式的后验概率分布p(p|x)，并且这个后验概率分布p(p|x)融合了观测样本x。也就是说共轭先验p(p)和后验概率分布p(p|x)具有相当的函数形式。

说点人话吧。。。

Beta分布是二项分布的参数p的共轭先验，也就是说，二项分布的参数p的共轭先验是一个Beta分布，其中，Beta分布中的两个参数a,b可以看作两个二项分布的参数p的先验知识，可以称为伪计数，例如 a, b = 2, 1, 这就意味着，二项分布的参数p的先验知识为：在三次实验中，a出现两次，b出现1次，也可以理解为发生了2次，没有发生的有1次。

后验概率也符合Beta分布：

Beta(p|a, b) + count(m1, m2) = Beta(p| a+m1, b+m2)

在二项分布的参数的先验分布的基础上，加上观测数据，就可以得到二项分布的参数p的后验概率分布也符合Beta分布。这里， m1, m2 分别表示对应于 x=1 和 x=0在观测数据中出现的次数。

话说，共轭先验中的参数即Beta分布中的两个参数a,b 是非常有意义的hyperparameter的解释，前面已经提到了，a,b 可以理解为在观测样本 (m1, m2)的基础上的先验知识，或者可以理解为伪计数，即在我们的先验知识中， x=1和x=0分别应该出现多少次，并且，这个先验知识的取值，对于后验概率的计算有比较大的影响。

二项分布的参数p的后验概率分布仍然符合Beta分布可以通过下面的公式推到进行证明：

下面给出上面公式的推导过程：

假定集合C是服从N Bernoulli分布的一个集合，其中c=1或者c=0，那么可以根据贝叶斯参数估计计算集合C 的后验参数估计：

 

所以，由上面的推导可以证明二项分布的参数p的后验概率分布也服从Beta分布。

其中，上面公式中的Z可以进行如下推导：


 

 

公式2中用到了一个Beta分布的公式Beta函数：


 

所以，公式2中

 

posted @ 2017-03-21 13:06  Thinkando  阅读(8546)  评论(0)  编辑  收藏  举报