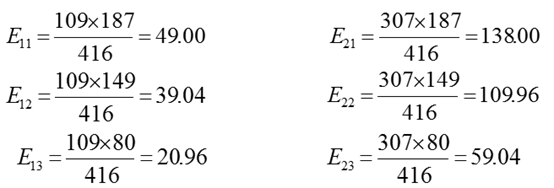第五章 χ2检验
第五章 χ2检验
一、χ2检验的定义
二、χ2检验与连续型资料假设检验的区别
三、χ2检验的用途
χ2 检验(Chi-square test)
对样本的频数分布所来自的总体分布是否服从某种理论分布或某种假设分布所作的假设检验，即根据样本的频数分布来推断总体的分布。
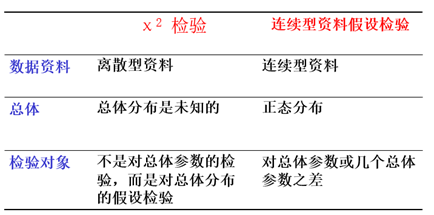
χ2检验与测量数据假设检验的区别
测量数据的假设检验，其数据属于连续变量，而χ2检验的数据属于点计而来的间断变量。
测量数据所来自的总体要求呈正态分布，而χ2检验的数据所来自的总体分布是未知的。
测量数据的假设检验是对总体参数或几个总体参数之差所进行的假设检验，而χ2 检验在多数情况下不是对总体参数的检验，而是对总体分布的假设检验。
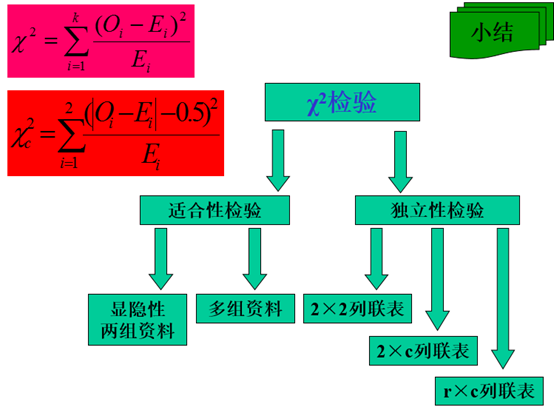
三、χ2检验的用途
适合性检验；独立性检验；同质性检验
适合性检验（吻合度检验）
是指对样本的理论数先通过一定的理论分布推算出来，然后用实际观测值与理论数相比较，从而得出实际观测值与理论数之间是否吻合。因此又叫吻合度检验。
独立性检验
是指研究两个或两个以上的计数资料或属性资料之间是相互独立的或者是相互联系的假设检验，通过假设所观测的各属性之间没有关联，然后证明这种无关联的假设是否成立。
同质性检验
在连续型资料的假设检验中，对一个样本方差的同质性检验，也需进行χ2 检验。
第一节： χ2检验的原理与方法
χ2检验的基本原理
χ2检验统计量的基本形式
χ2值的特点
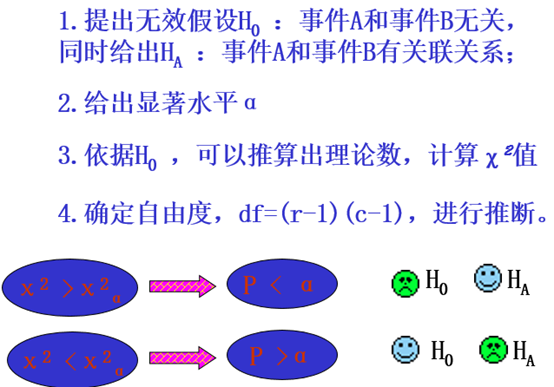
χ2检验的基本步骤
χ2检验的注意事项
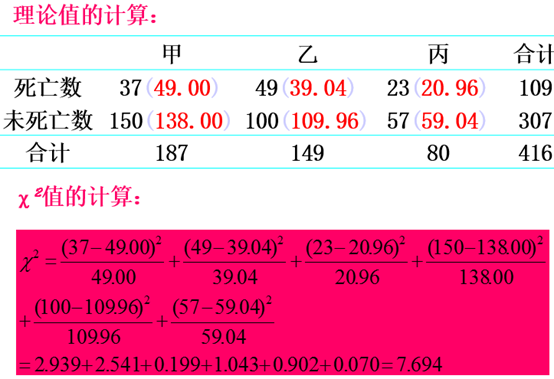
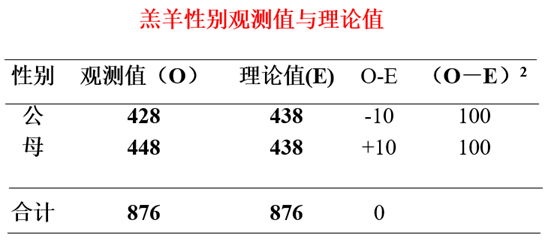
χ2检验就是统计样本的实际观测值与理论推算值之间的偏离程度。
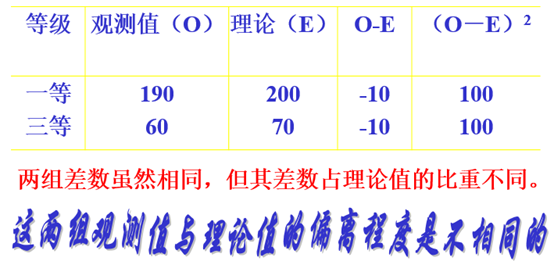
实际观测值与理论推算值之间的偏离程度就决定其χ2值的大小。理论值与实际值之间偏差越大， χ2值就越大，越不符合；偏差越小，χ2值就越小，越趋于符合；若两值完全相等时， χ2值就为0，表明理论值完全符合。
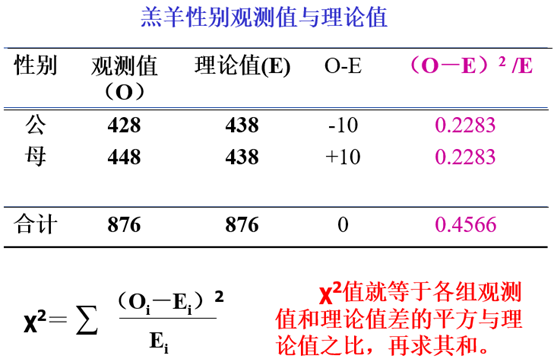
χ2值的特点，可加性，非负值，随O和E而变化
χ2值与概率P成反比， χ2值越小，P值越大，说明实际值与理论值之差越小，样本分布与假设的理论分布越相一致;
χ2值与概率P成反比， χ2值越小，P值越大，说明实际值与理论值之差越小，样本分布与假设的理论分布越相一致;
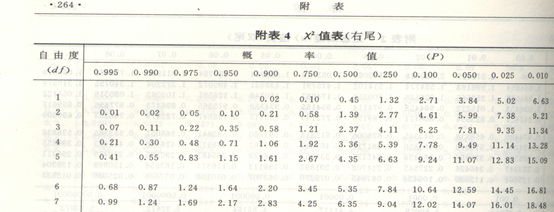
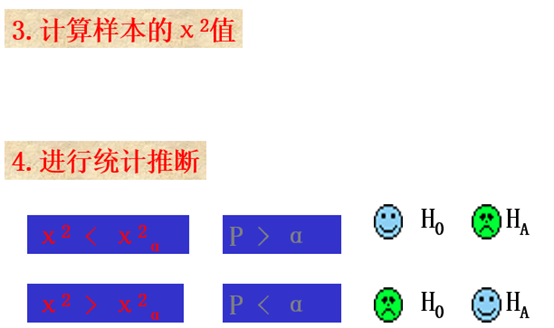
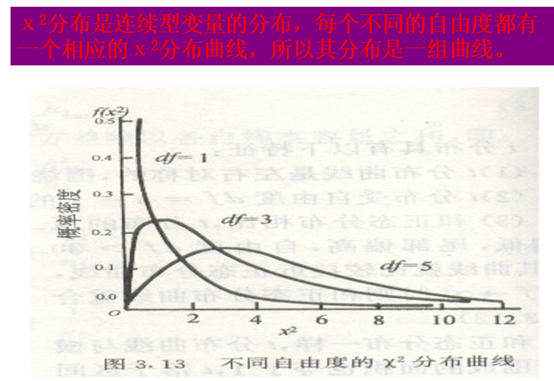
由于检验的对象－次数资料是间断性的，而χ2分布是连续型的，检验计算所得的χ2值只是近似地服从χ2分布，所以应用连续型的χ2分布的概率检验间断性资料所得的χ2值就有一定的偏差。
由次数资料算得的χ2均有偏大的趋势，即概率偏低。当df=1，尤其是小样本时，必须作连续性矫正。
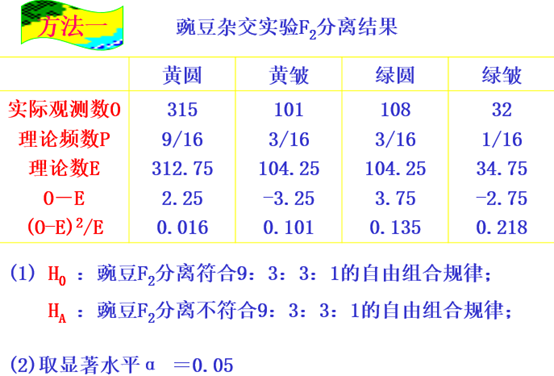
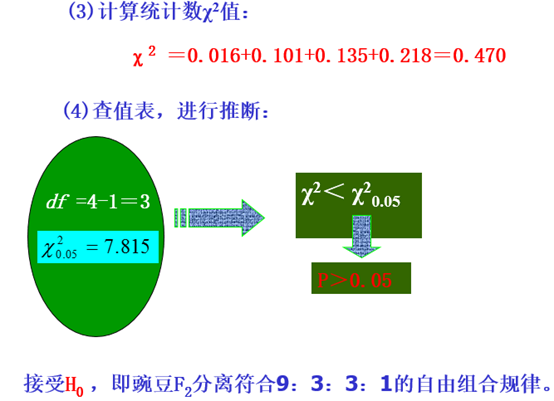
第二节：适合性检验
适合性检验：比较观测数与理论数是否符合的假设检验。
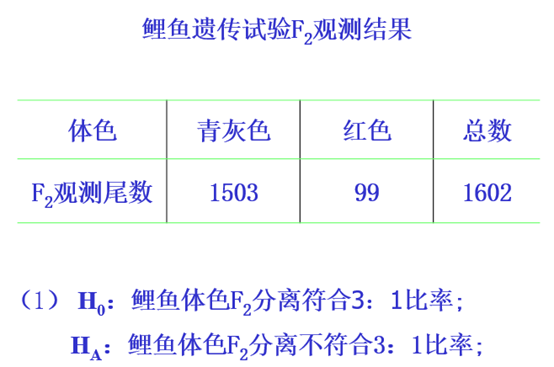
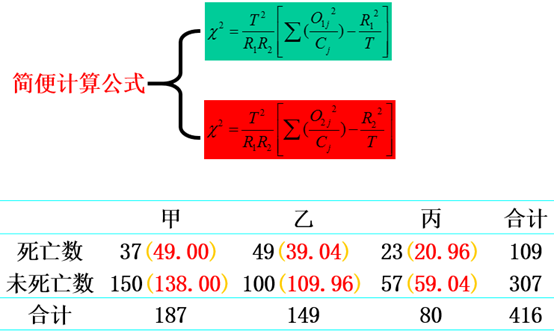
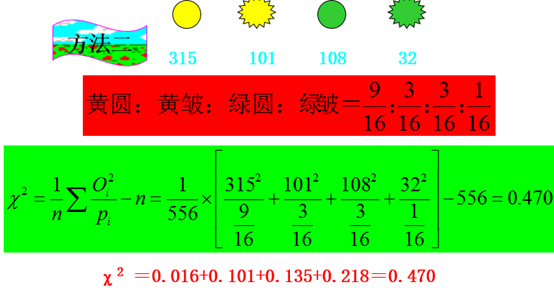
在遗传学中，有许多显、隐性比率可以划分为两组的资料，如欲测其与某种理论比率的适合性，则χ2值可用下表中的简式进行计算：
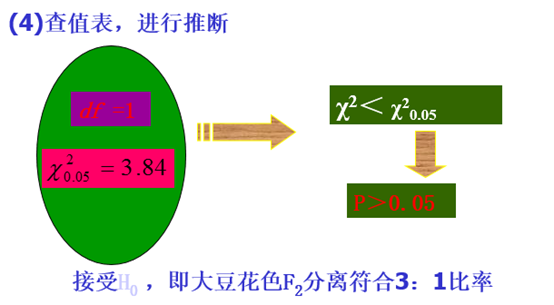
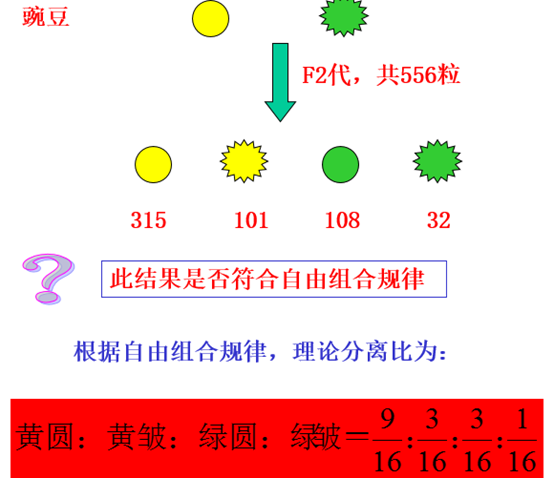
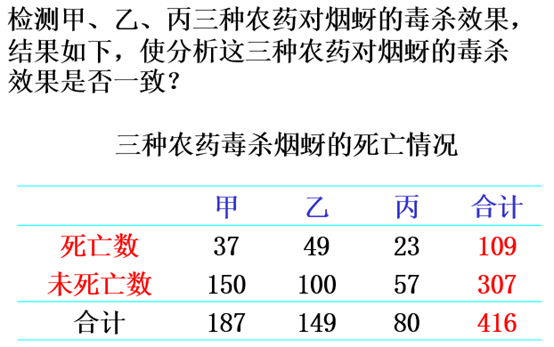
第三节：独立性检验
独立性检验的定义
2×2 列联表的独立性检验
2×ｃ列联表的独立性检验
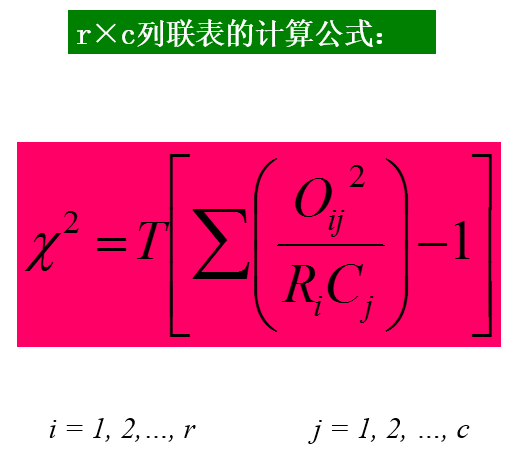
r×ｃ列联表的独立性检验
独立性检验（independence test）
又叫列联表（contigency table）χ2检验，它是研究两个或两个以上因子彼此之间是独立还是相互影响的一类统计方法。
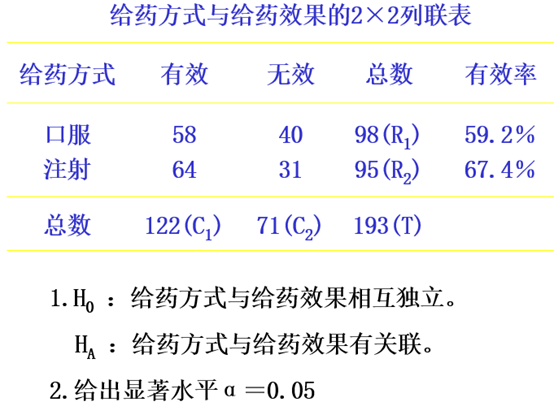
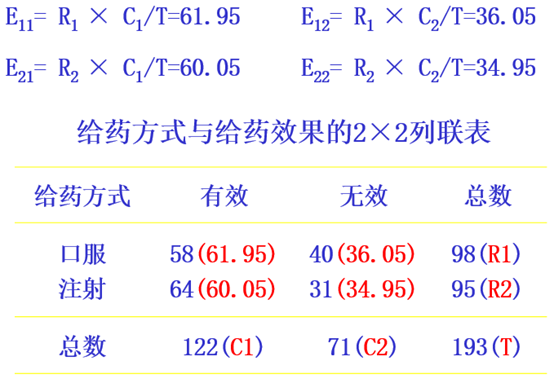
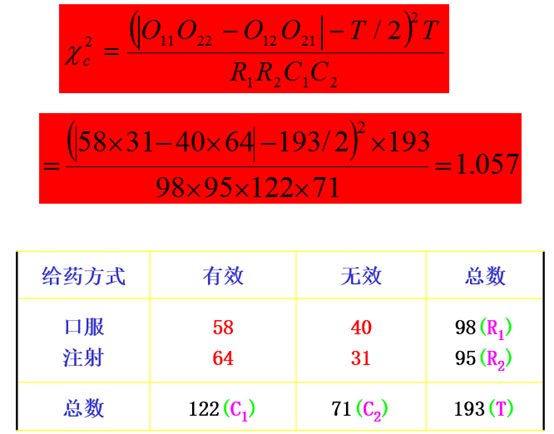
（一）2×2列联表的独立性检验
设A，B是一个随机试验中的两个事件，其中A可能出现r1 、r2个结果，B可能出现c1、c2个结果，两因子相互作用形成4格数，分别以O11 、O12 、O21 、O22表示，下表是2×2列联表的一般形式
