第四章 统计推断
第四章 统计推断
统计推断: 由一个样本或一糸列样本所得的结果来推断总体的特征(1 假设检验、2、参数估计)


第一节 假设检验的原理与方法
一 概念 : 假设检验(hypothesis test)又称显著性检验(significance test),就是根据总体的理论分布和小概率原理,对未知或不完全知道的总体提出两种彼此对立的假设,然后由样本的实际结果 ,经过一定的计算,作出在一定概率意义上应该接受的那种假设的推断。
小概率原理:
概率很小的事件在一次抽样试验中实际是几乎不可能发生的。

二 、假设检验的步骤








三 、双尾检验与单尾检验

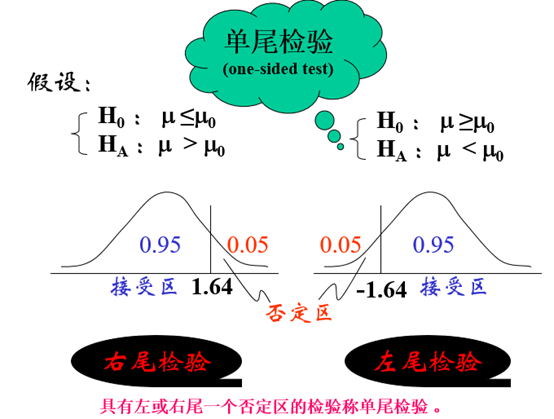

四 、两类错误

第一类错误(type I error),又称弃真错误或a 错误;
第二类错误( type II error ) ,又称纳伪错误或b 错误




第二节 样本平均数的假设检验
一、一个样本平均数的假设检验
适用范围:检验某一样本平均数x所属的总体平均数m是否和某一指定的总体平均数m0相同。若相同,则说明该样本属于这个以m0为平均数的指定总体;若不相同,则说明该样本所属的总体与这个指定总体( m0 )不同,即有显著或极显著差异。
1、总体方差σ2已知,无论n是否大于30都可采用u检验法








二、两个样本平均数的假设检验
适用范围:检验两个样本平均数x1和x2所属的总体平均数m1和m2是否来自同一总体。









试验设计:
- 成组数据平均数的比较
如果两个样本的各个变量是从各自总体中随机抽取的,两个样本之间的变量没有任何关联,即两个抽样样本彼此独立,则不论两样本的容量是否相同,所得数据皆为成组数据。两组数据以组平均数作为相互比较的标准,来检验其差异的显著性。
根据两样本所属的总体方差是否已知和样本大小不同而采用不同的检验方法。




















成对数据平均数的比较
将性质相同的两个样本(供试单位)配偶成对,每一对除随机地给予不同处理外,其他试验条件应尽量一致,以检验处理的效果,所得的观测值称为成对数据。




第三节 样本频率的假设检验




一、一个样本频率的假设检验

在二项分布中,事件A发生的频率 x/n称为二项成数,即百分数或频率。则二项成数的平均数和标准差分别为:







二、两个样本频率的假设检验


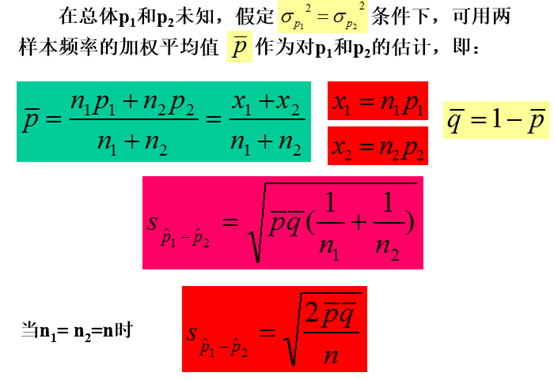









第四节:参数的区间估计与点估计
一、参数区间估计与点估计的原理
二、一个总体平均数的区间估计与点估计
三、两个总体平均数差数的区间估计与点估计
四、一个总体频率、两个总体频率差数的区间估计与点估计
参数的区间估计与点估计是建立在一定理论基础上的一种方法。
由中心极限定理和大数定律,只要抽样为大样本,不论其总体是否为正态分布,其样本平均数都近似服从正态分布N(μ,σ2/n)。




参数的区间估计也可用于假设检验。
置信区间是在一定置信度P=1-α下总体参数的所在范围,故对参数所进行的假设如果落在该区间内,就说明这个假设与真实情况没有不同,因而就可以接受零假设。
对参数所进行的假设如果落在该区间之外,就说明这个假设与真实情况有本质的不同,因而就否定零假设,接受备择假设。
无论区间估计还是点估计,都与概率显著水平α的大小联系在一起。
α越小,则相应的置信区间就越大,也就是说用样本平均数对总体平均数估计的可靠程度越高,但这时估计的精度就降低了。
在实际应用中,应合理选取概率显著水平α的大小,不能认为α取值越小越好。
二、一个总体平均数μ的区间估计和点估计
当为大样本时,不论总体方差σ2为已知或未知,可以利用样本平均数x和总体方差σ2作出置信度为P=1-α的总体平均数的区间估计为:

当样本为小样本且总体方差σ2未知时, σ2需由样本方差s2来估计,于是置信度为P=1-α的总体平均数μ的置信区间可估计为

Tа为正态分布下置信度P=1- α时的t临界值










例题 用高蛋白和低蛋白两种饲料饲养一月龄大白鼠,在三个月时,测定两组大白鼠的增重重量(g),
两组的数据分别为:
高蛋白组:134,146,106,119,124,161,107,83,113,129,97,123
低蛋白组:70,118,101,85,107,132,94
试进行置信度为95%时两种蛋白饲料饲养的大白鼠增重的差数区间估计和点估计。


四、一个总体频率p、两总体频率差数p1-p2的区间估计和点估计. 在置信度P=1- α下,对一 个总体频率P的区间估计为:


在进行两个总体频率p1-p2的区间估计和点估计时,一般应明确两个频率有显著差异才有意义。
在置信度为P=1-α下,两总体频率差数p1-p2的区间估计为







第五节 方差的同质性检验
所谓方差的同质性,就是指各个总体的方差是相同的。
方差的同质性检验就是要从各样本的方差来推断其总体方差是否相同
一、 一个样本方差的同质性检验












 浙公网安备 33010602011771号
浙公网安备 33010602011771号