第二章 试验资料的整理与特征数的计算
第二章 试验资料的整理与特征数的计算
一、试验资料的类型
对试验资料进行分类是统计归纳的基础。

一、数量性状资料
数量性状(quantitative character)是指能够以计数和测量或度量的方式表示其特征的性状。观察测定数量性状而获得的数据就是数量性状资料 (data of quantitative characteristics)。数量性状资料的获得有计数和测量两种方式,因而数量性状资料又分为计数资料和计量资料两种。
1、计数资料:指用计数方式获得的数量性状资料。在这类资料中,它的各个观察值只能以整数表示,在两个相邻整数间不得有任何带小数的数值出现,因此各观察值是不连续的,所以该类资料也称为非连续变量资料或间断变量资料或离散变量资料。
2、计量资料 :指用测量或度量法获得的数量性状资料,即用度、量、衡等计量工具直接测定获得的数据资料。其数据是用长度、重量、容积、温度、浓度等来表示,要带单位。这种资料的各个观测值不一定是整数,两个相邻的整数间可以有带小数的任何数值出现,其小数位数的多少由度量工具的精确度而定, 它们之间的变异是连续性的,因此计量资料也称为连续变量资料。
二、质量性状资料
质量性状(qualitative character)是指能观察到而不能直接测量的性状。观察质量性状而获得的数据就是质量性状资料(data of qualitative characteristics),也称为属性性状资料。这类性状本身不能直接用数值表示,要获得这类性状的数据资料,须对其观察结果作数量化处理,其方法有以下两种:
1、统计次数法
在一定的总体或样本中,根据某一质量性状的类别统计其次数,以次数作为质量性状的数据。例如,在研究豌豆的花色遗传时,红花与白花杂交,子二代中红花、紫花和白花的株数分类统计。这种由质量性状数量化得来的资料又叫次数资料。
2、评分法
对某一质量性状分成不同级别,对不同级别进行评分来表示其性状差异的方法。从而将质量性状进行数量化,以便统计分析。
二、试验资料的搜集

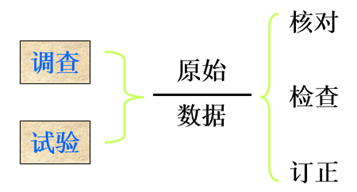
一、调查
调查是对已经存在的事情的资料按某种方案进行收集的方法。资料的调查又可以分为两种:普查和抽样调查。
1、普查
是对研究对象的全部个体逐一进行调查的方法。普查一般要求在一定的时间或范围进行,要求准确和全面。
2、抽样调查
是根据一定的原则从研究对象中抽取一部分具有代表性的个体进行调查的方法。通过抽样将获得的样本资料进行统计处理,然后利用样本的特征数对总体进行推断。生物学研究中,进行普查的情况较少,多数情况下还是进行抽样调查。
随机抽样必须满足2个条件:一是总体中每个个体被抽中的机会是均等的;二是总体中任意一个个体是相互独立的,是否被抽中不受其他个体的影响。
二、试验
试验是对已有的或没有的事物加以处理的方法。
常见的试验设计方法有:对比设计、随机区组设计、平衡不完全区组设计、裂区设计、拉丁方设计、正交设计、正交旋转设计等等。
试验设计须遵循的三大原则是:随机、重复和局部控制。
三、试验资料的整理
(一)原始资料的检查与核对
检查和核对原始资料的目的:确保原始资料的完整性和正确性。
(二)次数分布表
统计表的结构和要求:结构简单,层次分明,安排合理,重点突出,数据准确。

1 计数资料的整理
计数资料基本上采用单项式分组法进行整理。
特点:用样本变量自然值进行分组,每组用一个或几个变量值来表示。
2 计量资料的整理
计量资料一般采用组距式分组法。

(1) 求全距,又称极差(range):R=Xmax- Xmin
(2) 确定组数和组距(class boundary)

组距=全距/组数,
(3)确定组限(class limit)和组中值(class midvalue)

(4) 分组
确定好组数和各组上下限后,可按原始资料中各观测值的次序,将各个数值归于各组,计算各组的观测数次数、频率、累积频率,制成一个次数分布表。

(三)次数分布图和频率分布图
定义:把次数(频率)分布资料画成统计图形。
特点:直观、形象
包括:条形图bar chart又称柱形图 柱形之间要间隔一定的距离 
直方图 (histogram),又称矩形图 各组之间没有距离 
多边形图(polygon),又称折线图(broken-line chart)
饼图(pie chart)和散点图(scatter)
统计图绘制的基本要求:
(1)标题简明扼要,列于图的下方;
(2)纵、横两轴应有刻度,注明单位;
(3)横轴由左至右,纵轴由下而上,数值由小到大;图形长宽比例约5:4或6:5;
(4)图中需用不同颜色或线条代表不同事物时,应有图例说明。
特征数的计算
变量的分布具有两种明显的基本特征:集中性和离散性。
集中性 是变量在趋势上有着向某一中心聚集,或者说以某一数值为中心而分布的性质。
离散性 是变量有着离中分散变异的性质。
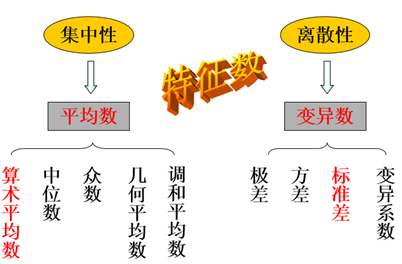
一、平均数
平均数 平均数是统计学中最常用的统计量,是计量资料的代表值,表示资料中观测数的中心位置,并且可作为资料的代表与另一组相比较,以确定二者的差异情况。
1. 算术平均数 (arithmetic mean)
定义:总体或样本资料中所有观测数的总和除以观测数的个数所得的商,简称平均数、均数或均值。

2. 中位数(median) (Md)
资料中所有观测数依大小顺序排列,居于中间位置的观测数称为中位数或中数。
3. 众数(mode) (M0)
资料中出现次数最多的那个观测值或次数最多一组的组中值或中点值。
注意:
(1)对于某些数据而言,如均匀分布,并不存在众数;
(2)对于某些数据存在两个或两个以上的众数;
(3)主要用来描述频率分布。
4. 几何平均数 (geometric mean)(G)
资料中有n个观测数,其乘积开n次方所得数值。

适用范围:几何均数适用于变量X为对数正态分布, 经对数转换后呈正态分布的资料。
5. 调和平均数 (harmonic mean) (H)
资料中各观测值倒数的算术平均数的倒数。

适用范围:主要用于反映生物不同阶段的平均增长率或不同规模的平均规模。
(三)算术平均数的重要性质
离均差之和等于零。

离均差平方和最小。

四)算术平均数的作用
(1)指出一组数据资料内变量的中心位置,标志着资料所代表性状的数量水平和质量水平。
(2)作为样本或资料的代表数与其他资料进行比较。
(3)通过平均数提供计算样本变异数的基本数据。
(4)用样本的平均数估计总体平均数。
(一)极差(全距,range)(R)
极差是数据分布的两端变异的最大范围,即样本变量值最大值和最小值之差,用R表示。它是资料中各观测值变异程度大小的最简便的统计量。
方差(Variance)
各个观测值与平均数的离差,即离均差。
平方和(SS)
平方和的平均数
方差(均方) (n-1 自由度)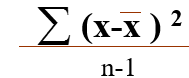

标准差(standard deviation, Sd)
样本方差带有原观测单位的平方单位,在仅表示一个资料中各观测值的变异程度而不作其它分析时,常需要与平均数配合使用,这时应将平方单位还原,即求出样本方差的平方根。

特点:1 标准差的大小,受多个观测数影响,如果观测数与观测数间差异较大,则离均差也大,因而标准差也大,反之则小。
2各观测数加上或减去一个常数,其标准差不变;
3各观测数乘以或除以一个常数a,其标准差扩大或缩小a倍。

表示变量分布的离散程度。
可以概括估计出变量的次数分布及各类观测数在总体中所占的比例。
估计平均数的标准误。
进行平均数的区间估计和变异系数计算。
(四)变异系数(coefficient of variability, CV )
定义:样本的标准差除以样本平均数,所得到的比值就是变异系数。

特点:是样本变量的相对变异量,不带单位。可以比较不同样本相对变异程度的大小。
用途:比较度量衡单位不同的多组资料的变异度。
比较均数相差悬殊的多组资料的变异度。


