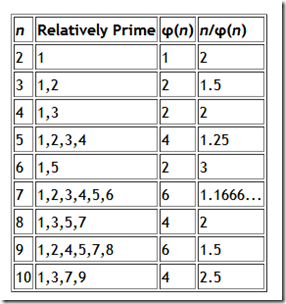
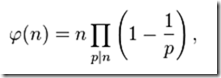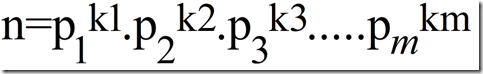欧拉函数φ(n)(有时也叫做phi函数)可以用来计算小于n 的数字中与n互质的数字的个数。
当n小于1,000,000时候,n/φ(n)最大值时候的n。
这里的是p是n的素因子,当素因子有相同的时候只取一个
任意一个正整数都能分解成若干个素数乘积的形式
如下所示:
long phi(int n){ long res=0; int pi=0; if(n==1) return 0; res = n; pi = 2; while(n!=1){ if(n%pi==0){ res*=(pi-1); res/=pi; while(n%pi==0){ n/=pi; } } pi++; } return res; }
上面res是存放φ(n)
是素因子的数更行res
由于素因子可能相同的
while(n%pi==0){ n/=pi; }
然而运行结果:
// 510510 5.539388020833333 // running time=270s483ms
这里要变量一百万次,内循环还要遍历,时间已经超过了欧拉工程的一分钟原则
参考网上程序,改成下面的形式:
long phi2(int n){ long res = 0; if(n==1) return 0; int pi=2; res = n; while(pi*pi <=n){ if(n%pi==0){ res*=(pi-1); res/=pi; while(n%pi==0){ n/=pi; } } pi++; } if(n>1){ res*=(n-1); res/=n; } return res; }
一个结束条件是while(n!=1)
一个结束条件是while(pi*pi<=n) n的素因子一定小于等于根号n,当pi大于根号n的时候的循环完全是拜拜浪费时间
此时你一定想到素数的循环,这里很类似
运行结果:
// 510510 5.539388020833333 // running time=1s292ms
时间少了很多
在题解报告中,看到用到素数
当这个数的是素数的时候,欧拉函数φ(n) = n-1
当不是素数时候,找出小于n的素数,且能不n整除的数是n的素因子
long phi3(int n){ long res = n; int pi=2; if(isPrime(n)||n==1) res = n-1; else{ while(pi<=n){ if(n%pi==0 &&isPrime(pi)){ res*=(pi-1); res/=pi; } pi++; } } return res; }
结果:
// 510510 5.539388020833333 // running time=1885s497ms
上面程序对找到的素因子,没有去除,同时循环是while(pi<=n),可以进一步优化
while(pi<=n){ if(n%pi==0 &&isPrime(pi)){ res*=(pi-1); res/=pi; while(n%pi==0){ n/=pi; } } pi++; }
结果:
// 510510 5.539388020833333 // running time=111s291ms
时间少了好多
while(pi*pi<=n){ if(n%pi==0 &&isPrime(pi)){ res*=(pi-1); res/=pi; // while(n%pi==0){ // n/=pi; // } } pi++; }
结果:
// 510510 5.539388020833333 // running time=4s531ms
然而while(pi*pi<=n) + 去除相同素因子 的,程序结果不对!!!
while(pi*pi<=n){ if(n%pi==0 &&isPrime(pi)){ res*=(pi-1); res/=pi; while(n%pi==0){ n/=pi; } } pi++; } if(n>1) res = res/n*(n-1);
这样就对了
结果:
// 510510 5.539388020833333 // running time=1s454ms
去重后,最后一个n也是符合条件的
这个时间竟然比第2个的时间还要长。
Python程序:
import time as time def phi(n): if n==1 :return 0 res = n pi = 2 while(pi*pi<=n): if n%pi==0: res=res/pi*(pi-1) while n%pi==0: n/=pi pi+=1 if n>1:res=res/n*(n-1) return res # 510510 # running time: 32.007999897 s if __name__ == '__main__': t0 = time.time() Max_n = 1000000 result= 1 value = 0.0 for n in range(2,Max_n): euler = phi(n) temp = n/(euler*1.0) if temp>value: value = temp result = n print result print "running time:",(time.time() - t0),'s'
全部的Java程序:
package project61; public class P69{ void run(){ long max_n = 1000000; double value = 0.0; long euler = 0; long N=0; for(int i=2;i<=max_n;i++){ euler = phi3(i); // System.out.println(i+" "+euler); double temp = (double)i/(euler*1.0); if(temp>value){ value = temp; N = i; } } System.out.println(N+" "+value); } long phi3(int n){ long res = n; int pi=2; if(isPrime(n)||n==1) res = n-1; else{ while(pi*pi<=n){ if(n%pi==0 &&isPrime(pi)){ res*=(pi-1); res/=pi; while(n%pi==0){ n/=pi; } } pi++; } if(n>1) res = res/n*(n-1); } return res; } // 510510 5.539388020833333 // running time=1885s497ms // 510510 5.539388020833333 // running time=111s291ms // 510510 5.539388020833333 // running time=4s531ms // 510510 5.539388020833333 // running time=1s454ms boolean isPrime(int num){ if(num==2||num==3||num==5||num==7) return true; if(num<=1||num%2==0||num%3==0) return false; for(int i=2;i<=Math.sqrt(num)+1;i++){ if(num%i==0) return false; } return true; } long phi2(int n){ long res = 0; if(n==1) return 0; int pi=2; int k =0; res = n; while(pi*pi <=n){ if(n%pi==0){ res*=(pi-1); res/=pi; while(n%pi==0){ n/=pi; } } pi++; } if(n>1){ res*=(n-1); res/=n; } return res; } // 510510 5.539388020833333 // running time=1s292ms long phi(int n){ long res=0; int pi=0; if(n==1) return 0; res = n; pi = 2; while(n!=1){ if(n%pi==0){ res*=(pi-1); res/=pi; while(n%pi==0){ n/=pi; } } pi++; } return res; } // 510510 5.539388020833333 // running time=270s483ms public static void main(String[] args){ long start = System.currentTimeMillis(); new P69().run(); long end = System.currentTimeMillis(); long time = end - start; System.out.println("running time="+time/1000+"s"+time%1000+"ms"); } }