人生路径规划-蒙特卡洛树搜索

　 1、人的一生几十年，总会有那么几个关键节点需要决策，常见的有：

•    高中学文科还是理科？
•    高考考那所大学？  学什么专业？
•    本科毕业后，要不要继续读硕士？ 硕士毕业后要不要继续读博士？
•    毕业后在国内发展，还是去国外发展？
•    每年都有大量的公司去学校校招，该选那家公司就业了？甚至是自己单干创业了？
•    每年都有大量的岗位招人，该去应聘哪些岗位了？
•    工作几年了，应该在哪买房了？ 买完房要不要立即考虑结婚生子的事了？

      这些都是人生的重大的路口，每个分支都有可能改变人生的轨迹。对于普通的个体而言，在关键的分岔口前怎么选择才能达到最优了？

      回顾一下之前TSP的解决思路：以树的形式列举所有可能的路线，然后从“终点”开始往根节点回溯，每遇到一个分支就PK另一个相连分支的成本，通过二选一的形式找出成本最低的分支后继续往上回溯（感觉好残酷，类似大厂内部不同团队做同样的产品，最终只能有团队一个活着），直到达到根节点！蒙特卡洛树搜索的思路基本一致，也是从某个节点开始expansion，计算这个分支的成本，并和另一个相连的分支PK，成本低的分支保留，继续向上回溯。整个算法的核心流程如下：

•     selection: 选择某个分支
•     expansion：从这个分支的叶子节点扩展
•     simulation:  从这个叶子节点模拟后续的发展路径
•     backpropagation:  往上回溯，看看这个分支的成本或收益和另一个分支比咋样，要不要保留这个分支

      

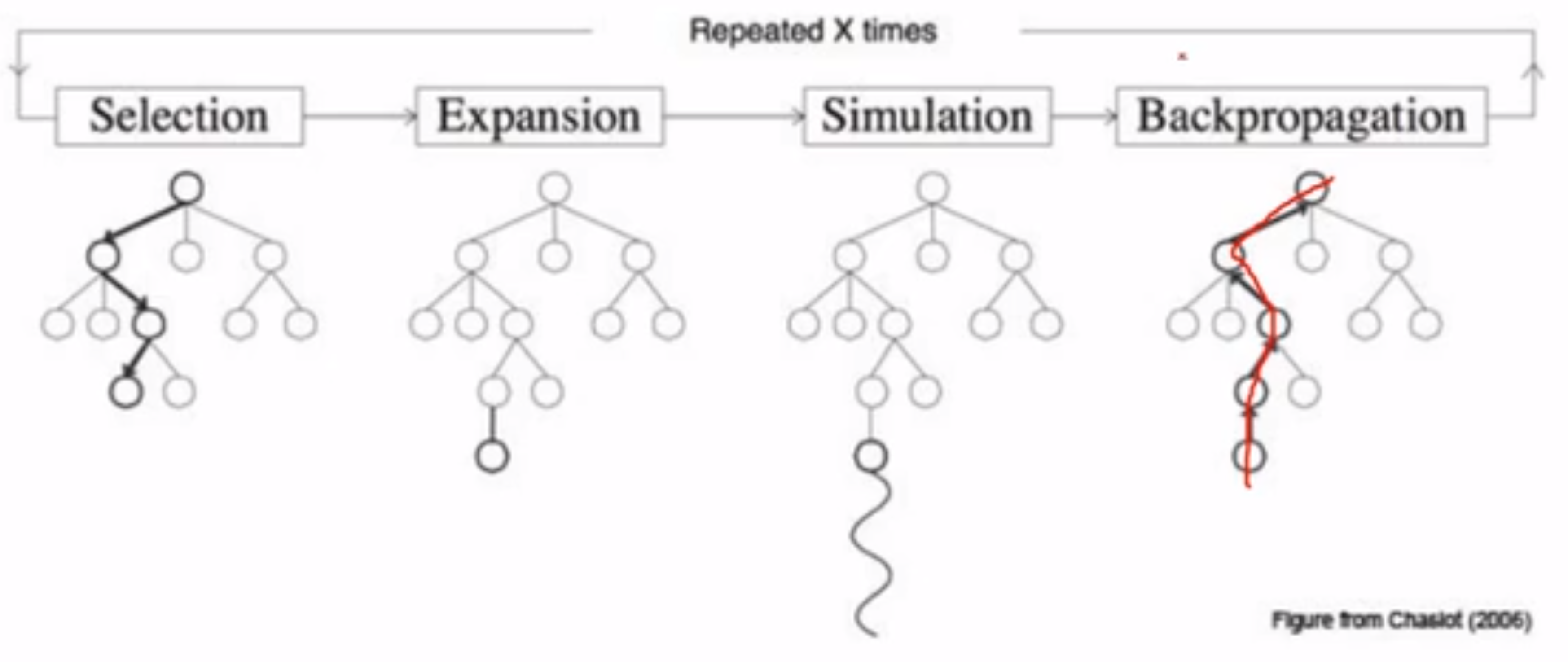
      怎么样？是不是很像人生的决策？ 读高中的时候不知道选文科还是理科，读大学不知道学数学、物理、化学、生物、计算机、环境、医学等，都可以参考这种思路，穷举所有的可能分支，计算每条分支的预取收益或成本，最终选择最优的那条！比如高中读理科，大学学医学，毕业做医生是一条路径；高中读理科、大学学计算机，毕业当码农又是一条路径。这两条路径那条的收益高、成本低了? 

　　2、（1）手动遍历前先介绍一下整个过程的核心计算公式：UCB1（Upper Confidence Bound，上置信区间）公式来计算一个节点的”潜力“：UCB1越大，说明该节点的潜力越大，后续就从该节点继续分叉（这也是本算法的精要所在：面临多个选择的时候选择最优的路线，节约后续的时间成本），其他有共同父节点的相邻节点就不要了！那么这个公式每个变量的含义是啥？ 为啥又能代表该节点的潜力了？

        （2）公式如下：UCB1(Si)代表Si节点的“潜力值”，是Si状态的平均value（下面会介绍具体的计算方法），N是Si状态父节点的考察次数，ni是Si状态的考察次数；可以看出“潜力值”是由Si状态平均值和考察次数决定的：

• 平均值代表的是胜率高/价值大，意味着最后赢的概率较大，当然应该多花些精力分析其后续走法。
• 被考察次数少的节点意味着该节点（状态）尚未经过充分研究，有成为黑马的可能。（1）通过logN让考察次数的权重产生一定比例的“折损”；比如N=0的时候是无穷大，肯定要考察该点；N增加，这部分的权重并不会线性增加（可以看看logN的函数图就知道了），再除以子节点的考察次数、开平方后，数值会“直线”下降；这里可以看出考察次数的权重被严格限制，N和ni越大，这部分的权重越小！（2）N取父节点的考察次数，ni取自己的考察次数。N越大，父节点被考察越多；ni越小，自己被考察越少，说明父节点的N是被其他子节点撑大的（其他子节点已经被考察多次了），logN/ni  这个值就越大，说明自己自己被考察的少，兄弟节点被考察的多，自己的潜力还没被充分挖掘，成为“黑马”的可能性也就越大！
• 平均值低、考察次数又多的点，说明已经“吃干榨尽”，没啥利用价值了，可以直接忽略丢弃，后续用再考虑了继续分叉了，借此大量减少分支的计算，加快计算速度！
• C值越大，考察次数的权重也就越大，潜力值就越倾向于考察次数；

          

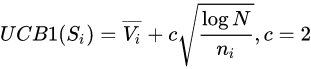
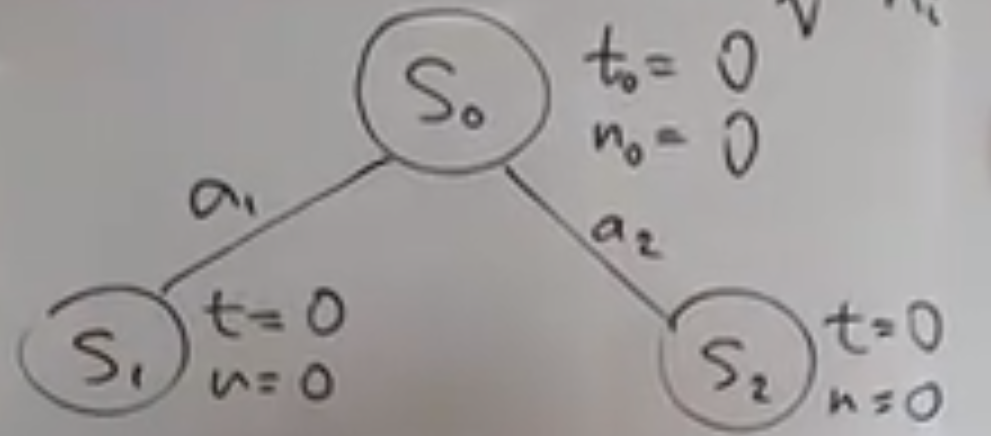
         （3）现在手动开始考察每个状态：

•    初始状态如下：S0是根状态，S1和S2是两个不同的下一个状态。初始的考察次数、value都是0；

         

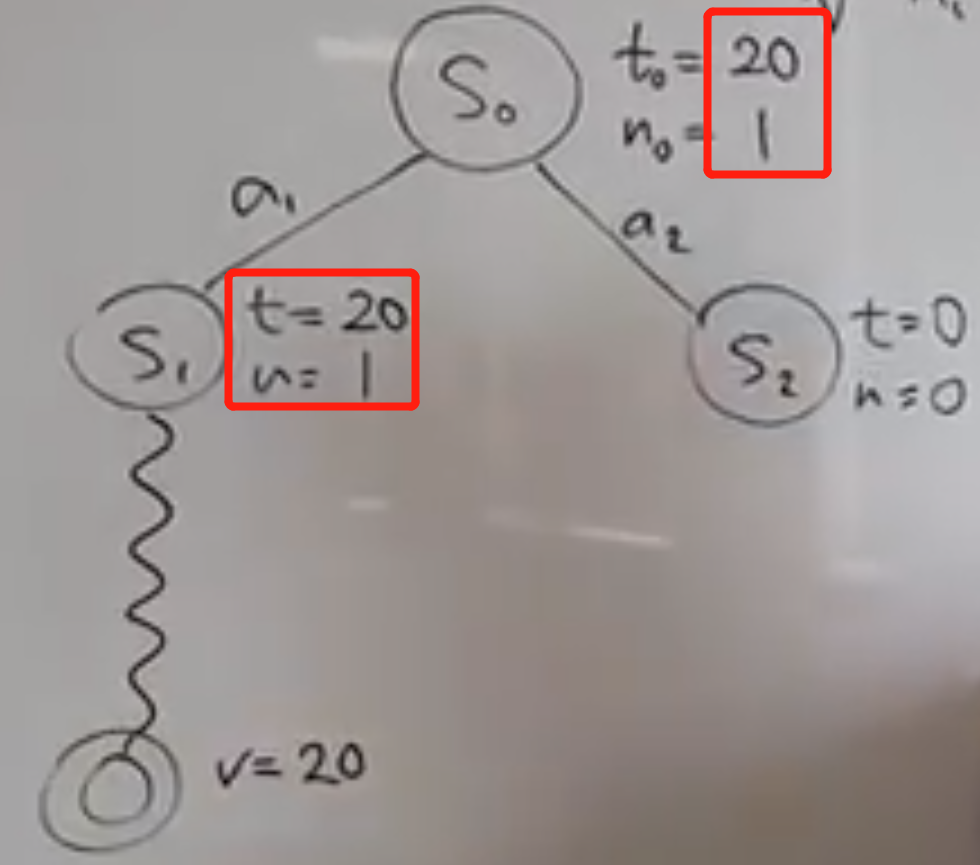
•     这是选S1还是S2没区别，随机选S1扩展吧。这是个叶子节点，并且还未考察过，就从这个节点开始rollout；假设最终的value=20（这里的value可以是多次尝试后的收益、赢的次数/概率、资产收益等），此时需要往上回溯把S1和S0的状态和value都更改：如图中标红的部分，至此算法第一步迭代已经完成；站在业务角度：父节点相当于部门的leader，子节点相当于部门的员工。考察次数当相当于员工的作业成本，value相当于员工的收益。作为部门leader，下属的成本和收益肯定也是要算到leader头上的，这就考验leader的管理水平了！

         

• 第一轮迭代完成，需要继续下一次迭代。问题又来了，该选那个状态继续了？ 此时就要计算不同状态的UCB1值了。很明显，S2的UCB1比S1大，此时从S2继续迭代；

        

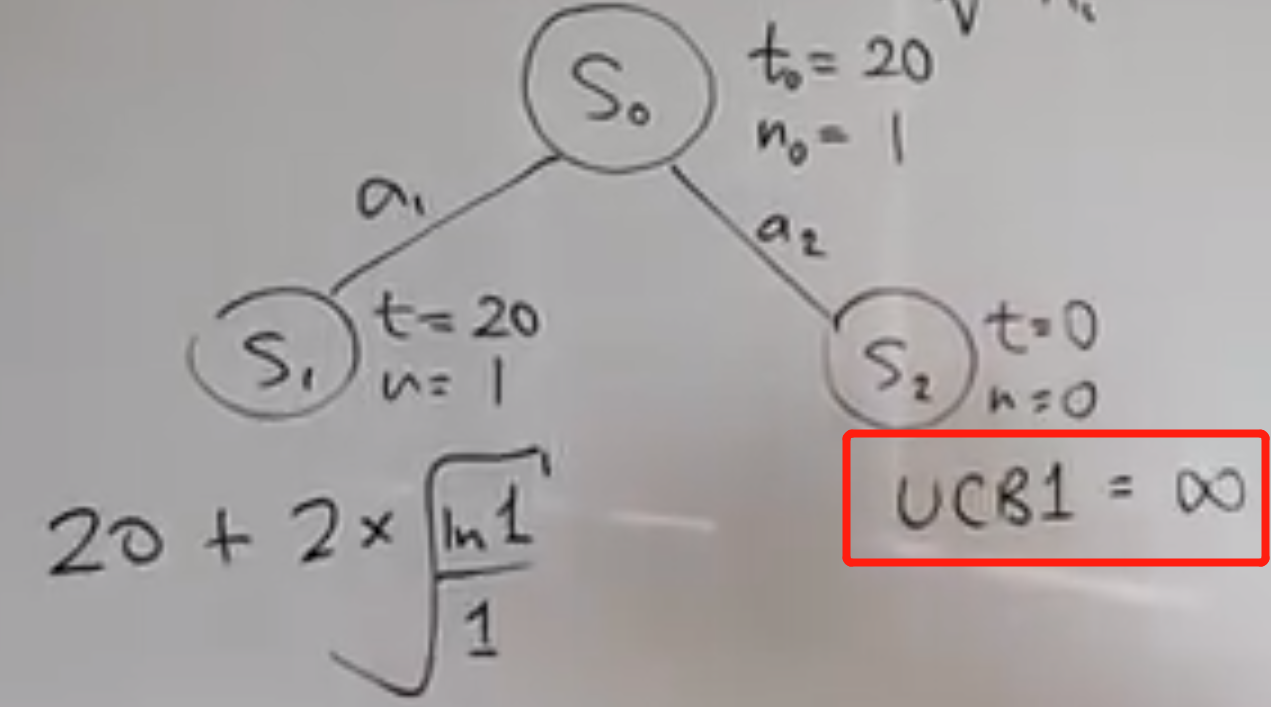
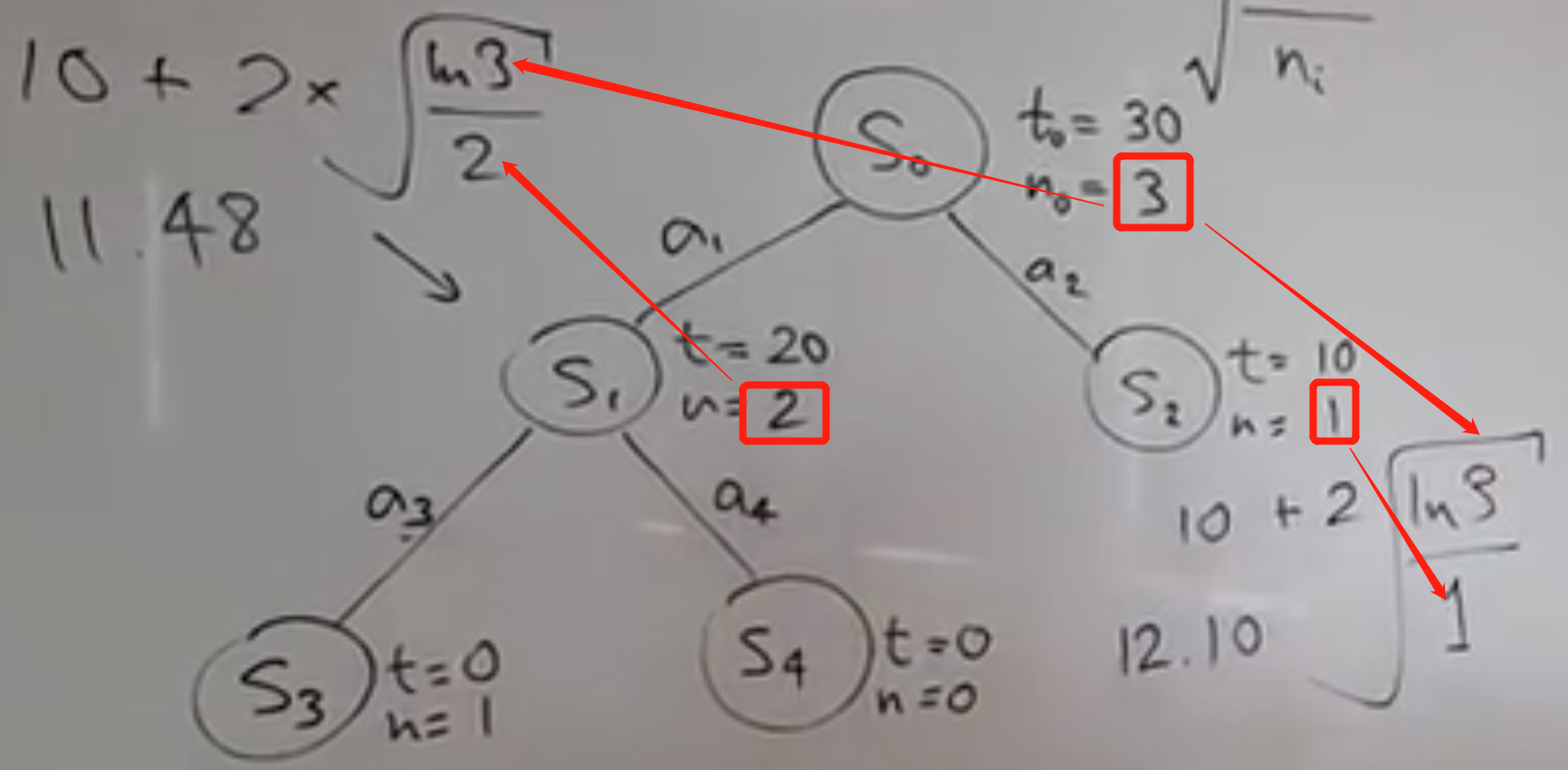
       从S2开始rollout，假设value=10，此时要往上回溯：跟新S2和S0的value和考察次数（都是累加），结局看红框框的地方：

       

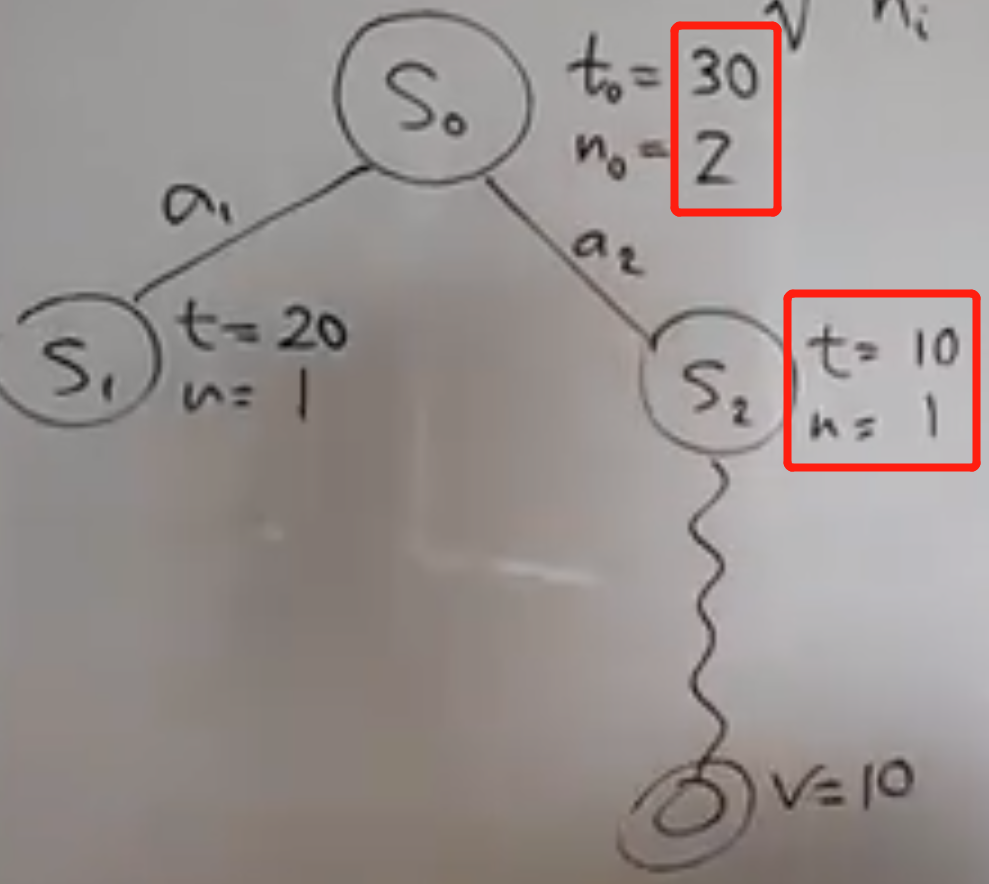
      第2轮迭代就此完成；接下来要进行第3次迭代，还是面临同样的问题：从S1还是S2开始了？老办法：看看UCB1的值！选择潜力值大的点下手！计算S1和S2的UCB1（注意，logN用的是父节点的考察次数），明显S1的比S2大，接着从S1开始扩展（expansion）；

      

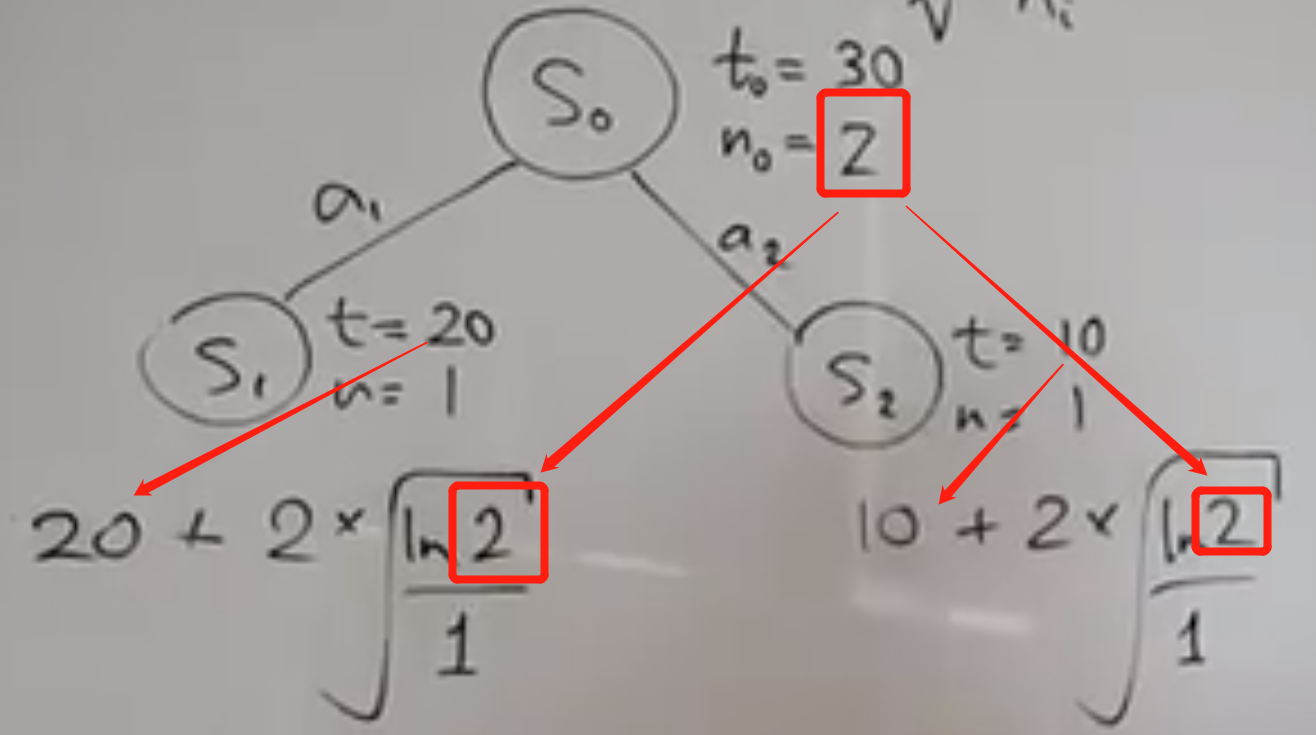
•   S1扩展出了S3和S4，此时两个节点的UCB1一样，随机从S3开始rollout。假设这次的value=0，那么往上回溯的时候S1和S0的value不变，考察次数分别+1，已经标红；第4次迭代就此结束；

      

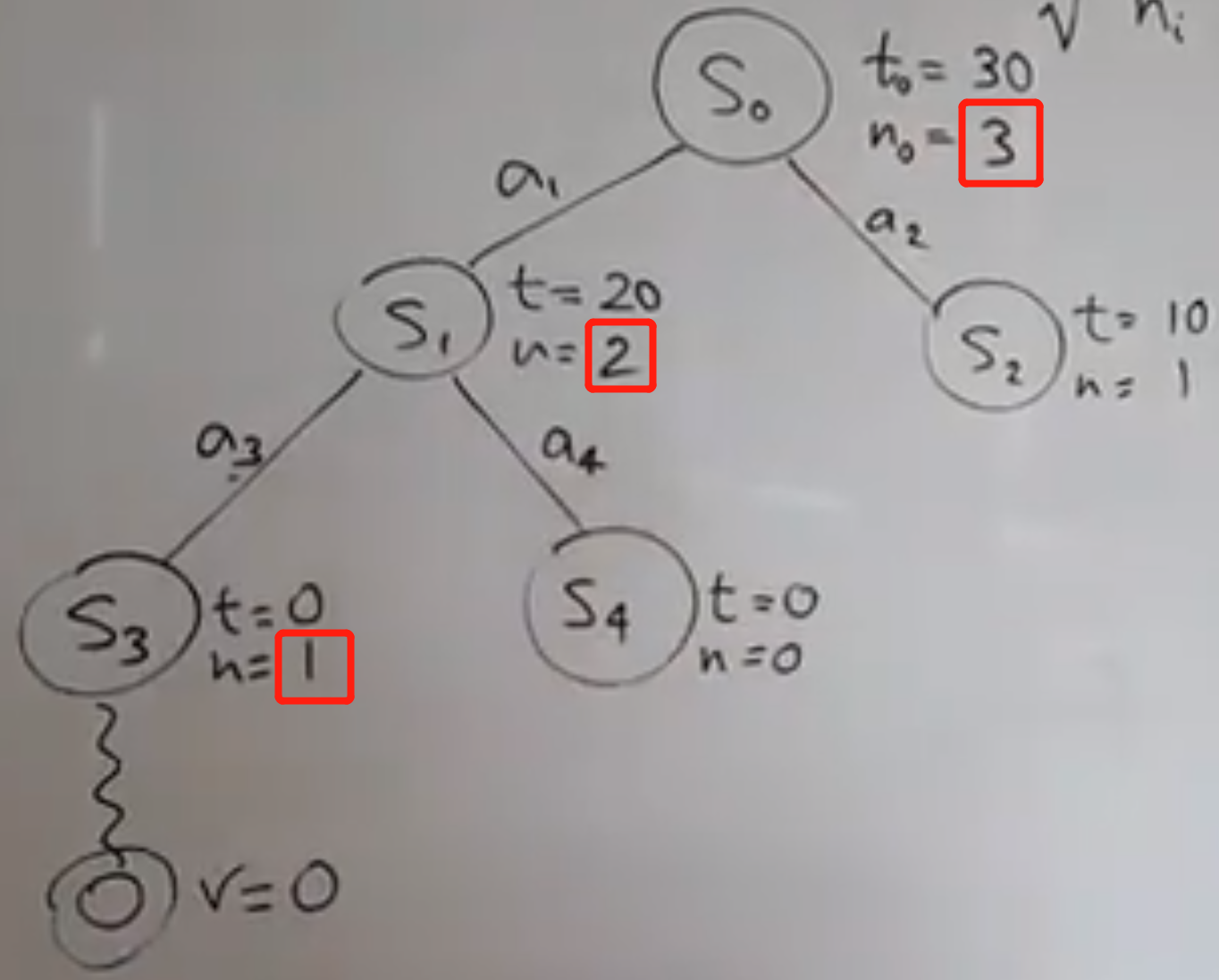
•      这里假设S4状态已经结束，不再rollout和expansion，第5次迭代又从哪开始了？ 只能回到上一层的S1和S2继续比较；因为刚才S1考察值更新，UCB1值肯定要变的，此时根据公式重新计算得到：11.48；注意：logN用的是根节点的S0的考察次数，此时是3；ni是自己的考察次数，此时是2；value是平均值，用总value除以自己的总考察次数，为20/2=10；同样的方法计算S2的UCB1，为12.10，比S1的大，下次从S2开始expansion；

       

•       从S2继续expansion的结果如下：分裂出S5和S6，两种状态都一样，随机选S5开始rollout，假设value=14，往上回溯S2和S0的value、考察次数（已经标红）！然后选择S6节点rollout、得到value后继续计算UCB1，对比S5和S6的UCB1，选择下一个expansion的节点！

       

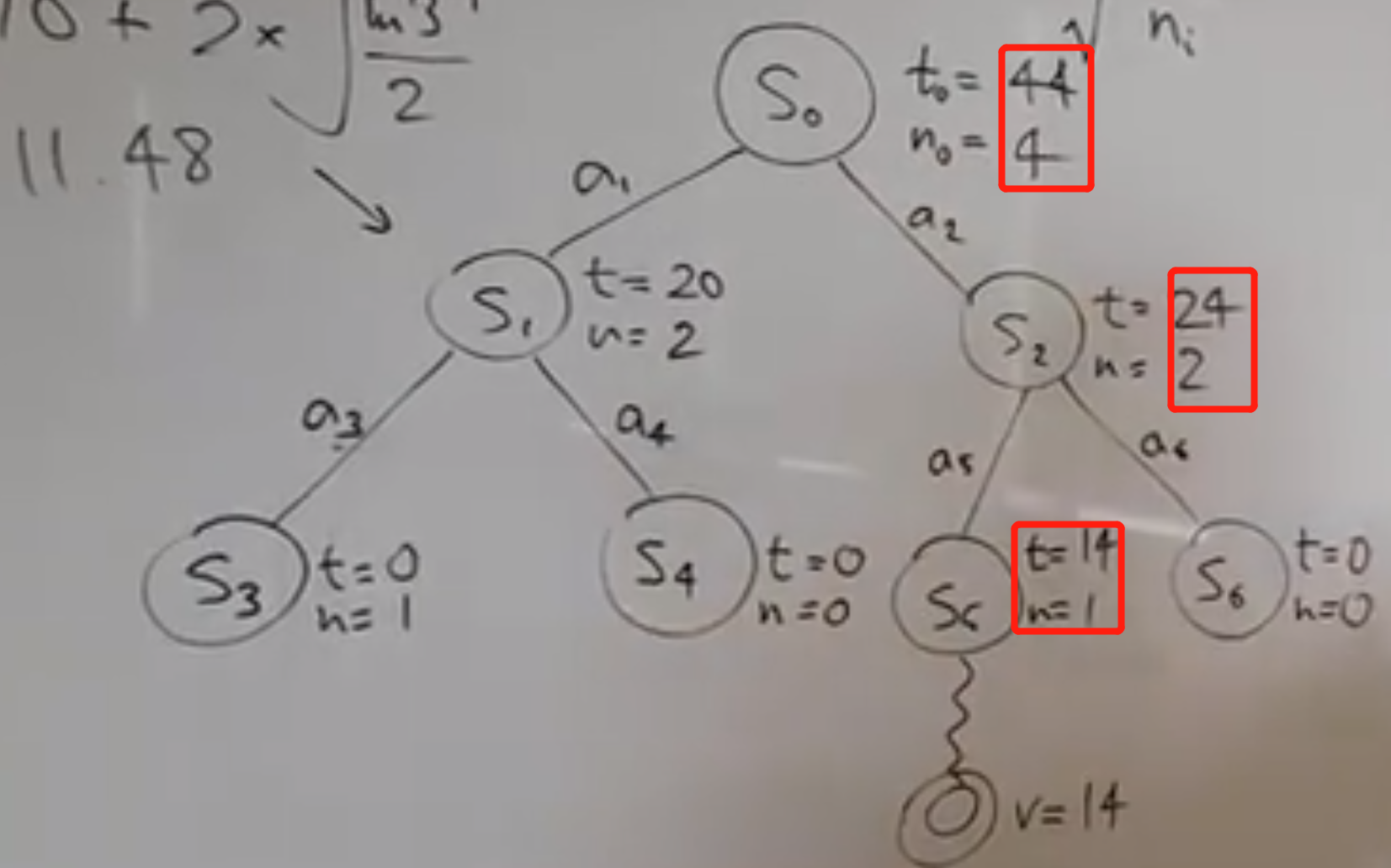
•  如此这般的往复迭代，什么时候才是尽头了？限制迭代次数或迭代时间！就目前的现状看，由于S2的潜力值是24，比S1的20大，但次数和S1是相同的，建议从S2走！

      3、回到本文刚开始抛出的问题：怎么选择才能让人生后续的发展最优了？ 这里就需要大量样本了（实际上很多人很是这么干的，只是没系统性地总结和提炼成算法）：

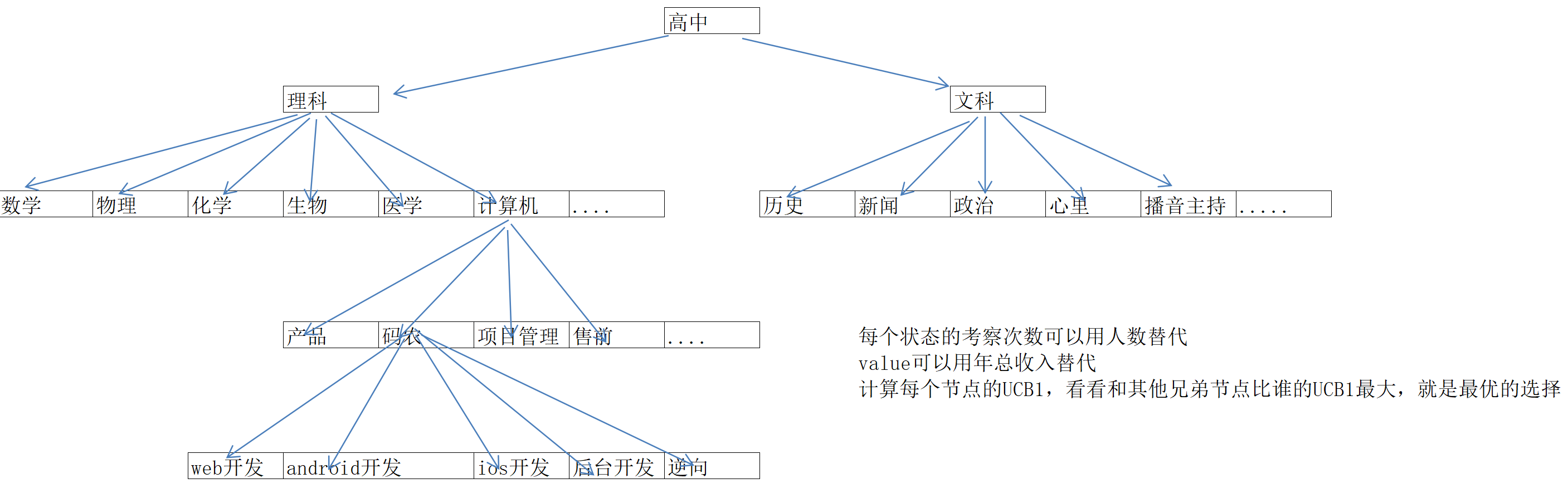
•       从高中（也就是根节点开始），统计不同选择后不同的收益，比如多少人选择理科（相当于节点被考察的次数），毕业后第一分工作的收入（相当于rollout的value）；选择UCB1高的节点继续expansion；比如理科节点的UCB1比文科节点的UCB1高，继续从理科节点expansion，这次分裂就看专业了；
•       根据计算机、生物、化学、物理、数学等不同专业的就学人数和毕业工资，再次对比不同专业的（也就是不同节点）的UCB1值，继续选择UCB1高的节点expansion；近些年互联网是热门，应届同学的待遇水涨船高，秒杀其他专业，这里选择计算机继续expansion
•       互联网也又很多工种，比如研发、产品、运维、销售、项目管理等；那么工种才是最有前途的了？ 继续根据人数和待遇计算不同工种的UCB1；这里假设码农的UCB1最高，继续从码农节点expansion
•       码农也分很多种，比如web前端、Android开发、IOS开发、后台发开、大数据开发、数据挖掘分析，还有我这种对逆向感兴趣的技术人员，用同样的方式计算不同岗位的UCB1，依次类推，肯定能找到最优钱途的位置！

         

 

 

 

参考：1、https://www.bilibili.com/video/BV1CJ411A7K9/?spm_id_from=333.788.videocard.0   大约从3:30开始演示演示算法过程

           2、https://zhuanlan.zhihu.com/p/43758287  蒙特卡洛树搜索 - 以蛮力对抗智慧

          3、https://juejin.cn/post/6844904054527623182  蒙特卡洛树搜索入门