K-SVD字典学习及其实现（Python）

算法思想

算法求解思路为交替迭代的进行稀疏编码和字典更新两个步骤. K-SVD在构建字典步骤中，K-SVD不仅仅将原子依次更新，对于原子对应的稀疏矩阵中行向量也依次进行了修正. 不像MOP，K-SVD不需要对矩阵求逆，而是利用SVD数学分析方法得到了一个新的原子和修正的系数向量.

固定系数矩阵X和字典矩阵D，字典的第\(k\)个原子为\(d_k\)，同时\(d_k\)对应的稀疏矩阵为\(X\)中的第\(k\)个行向量\(x^k_T\). 假设当前更新进行到原子\(d_k\)，样本矩阵和字典逼近的误差为：

\[\|Y - DX\|^2_F = \|Y - \sum\limits^K_{j=1}d_jx^j_T\|^2_F = \|(Y - \sum\limits_{j\neq k}d_jx^j_T) - d_kx^j_T\|^2_F = \|E_k -d_kx^k_T\|^2_F \]

在得到当前误差矩阵\(E_k\)后，需要调整\(d_k\)和\(X^k_T\)，使其乘积与\(E_k\)的误差尽可能的小.

如果直接对\(d_k\)和\(X^k_T\)进行更新，可能导致\(x^k_T\)不稀疏. 所以可以先把原有向量\(x^k_T\)中零元素去除，保留非零项，构成向量\(x^k_R\)，然后从误差矩阵\(E_k\)中取出相应的列向量，构成矩阵\(E^R_k\). 对\(E^R_k\)进行SVD（Singular Value Decomposition）分解，有\(E^R_k = U\Delta V^T\)，由\(U\)的第一列更新\(d_k\)，由\(V\)的第一列乘以\(\Delta (1,1)\)所得结果更新\(x^k_R\).

Python实现

import numpy as np
from sklearn import linear_model
import scipy.misc
from matplotlib import pyplot as plt


class KSVD(object):
    def __init__(self, n_components, max_iter=30, tol=1e-6,
                 n_nonzero_coefs=None):
        """
        稀疏模型Y = DX，Y为样本矩阵，使用KSVD动态更新字典矩阵D和稀疏矩阵X
        :param n_components: 字典所含原子个数（字典的列数）
        :param max_iter: 最大迭代次数
        :param tol: 稀疏表示结果的容差
        :param n_nonzero_coefs: 稀疏度
        """
        self.dictionary = None
        self.sparsecode = None
        self.max_iter = max_iter
        self.tol = tol
        self.n_components = n_components
        self.n_nonzero_coefs = n_nonzero_coefs

    def _initialize(self, y):
        """
        初始化字典矩阵
        """
        u, s, v = np.linalg.svd(y)
        self.dictionary = u[:, :self.n_components]

    def _update_dict(self, y, d, x):
        """
        使用KSVD更新字典的过程
        """
        for i in range(self.n_components):
            index = np.nonzero(x[i, :])[0]
            if len(index) == 0:
                continue

            d[:, i] = 0
            r = (y - np.dot(d, x))[:, index]
            u, s, v = np.linalg.svd(r, full_matrices=False)
            d[:, i] = u[:, 0].T
            x[i, index] = s[0] * v[0, :]
        return d, x

    def fit(self, y):
        """
        KSVD迭代过程
        """
        self._initialize(y)
        for i in range(self.max_iter):
            x = linear_model.orthogonal_mp(self.dictionary, y, n_nonzero_coefs=self.n_nonzero_coefs)
            e = np.linalg.norm(y - np.dot(self.dictionary, x))
            if e < self.tol:
                break
            self._update_dict(y, self.dictionary, x)

        self.sparsecode = linear_model.orthogonal_mp(self.dictionary, y, n_nonzero_coefs=self.n_nonzero_coefs)
        return self.dictionary, self.sparsecode


if __name__ == '__main__':
    im_ascent = scipy.misc.ascent().astype(np.float)
    ksvd = KSVD(300)
    dictionary, sparsecode = ksvd.fit(im_ascent)
    plt.figure()
    plt.subplot(1, 2, 1)
    plt.imshow(im_ascent)
    plt.subplot(1, 2, 2)
    plt.imshow(dictionary.dot(sparsecode))
    plt.show()

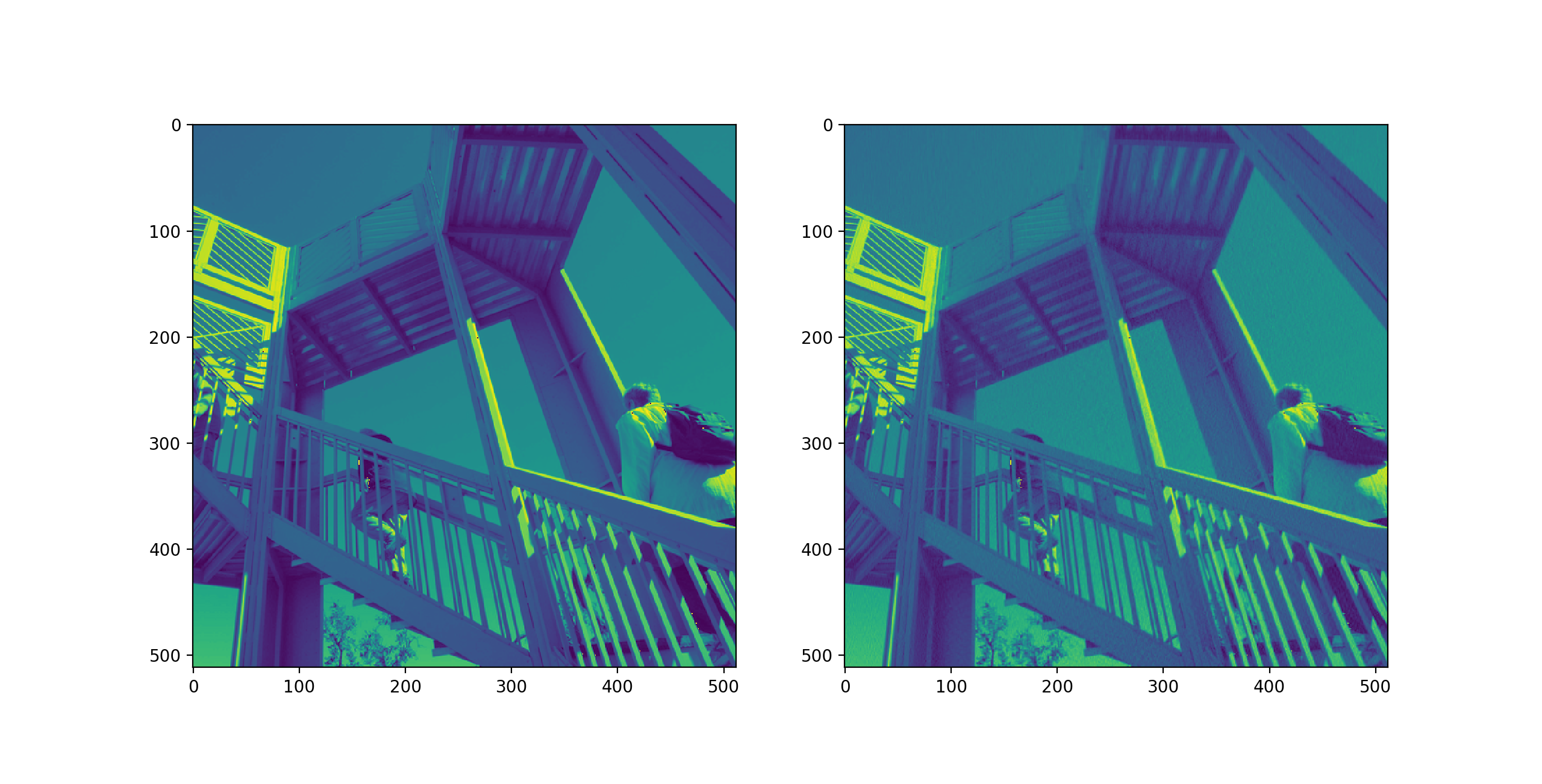
运行结果：