单纯形法MATALAB实现

参考单纯形法的步骤，MATALAB中的实现如下（求极小值）：
注：对于极大值的求解，只需要对目标函数添加负号，求解出来的\(X\)，再带入原目标函数即可。

function [ X, z ] = simplex( A, b, C )
% 单纯形法的实现
% X: 目标函数的最优解
% z: 目标函数的极小值
% A: 约束函数的系数矩阵
% b: 约束函数的常数列向量
% C: 目标函数的系数向量
[m, n] = size(A);
BIndex = n - m  + 1 : n;            % 基向量下标集合
NIndex = 1 : n - m;                 % 非基向量下标集合
flag = 1;
if (n < m)
    disp('系数矩阵不符合要求！')
else
    while flag
        B = A(:, BIndex);           % 基矩阵
        N = A(:, NIndex);           % 非基矩阵
        cb = C(BIndex);             % 基矩阵对应的目标值cb
        cn = C(NIndex);             % 非基矩阵对应的目标值cn
        xb = B \ b;
        X = zeros(1, n); X(BIndex) = xb;
        z = cb * xb;                    % 目标函数值
        sigma = cn - cb / B * N;        % 判别数
        [v, k] = min(sigma);            % k是进基向量下标
        if v > 1e-5
            flag = 0;
            disp('已找到最优解：')
        else
            [~, l] = min((B \ b) ./ (B \ A(:, k))); l = BIndex(l);      % l是出基向量下标
            BIndex(BIndex == l) = k;                % 更新基向量下标集合
            NIndex(NIndex == k) = l;                % 更新非基向量下标
        end
    end
end
end

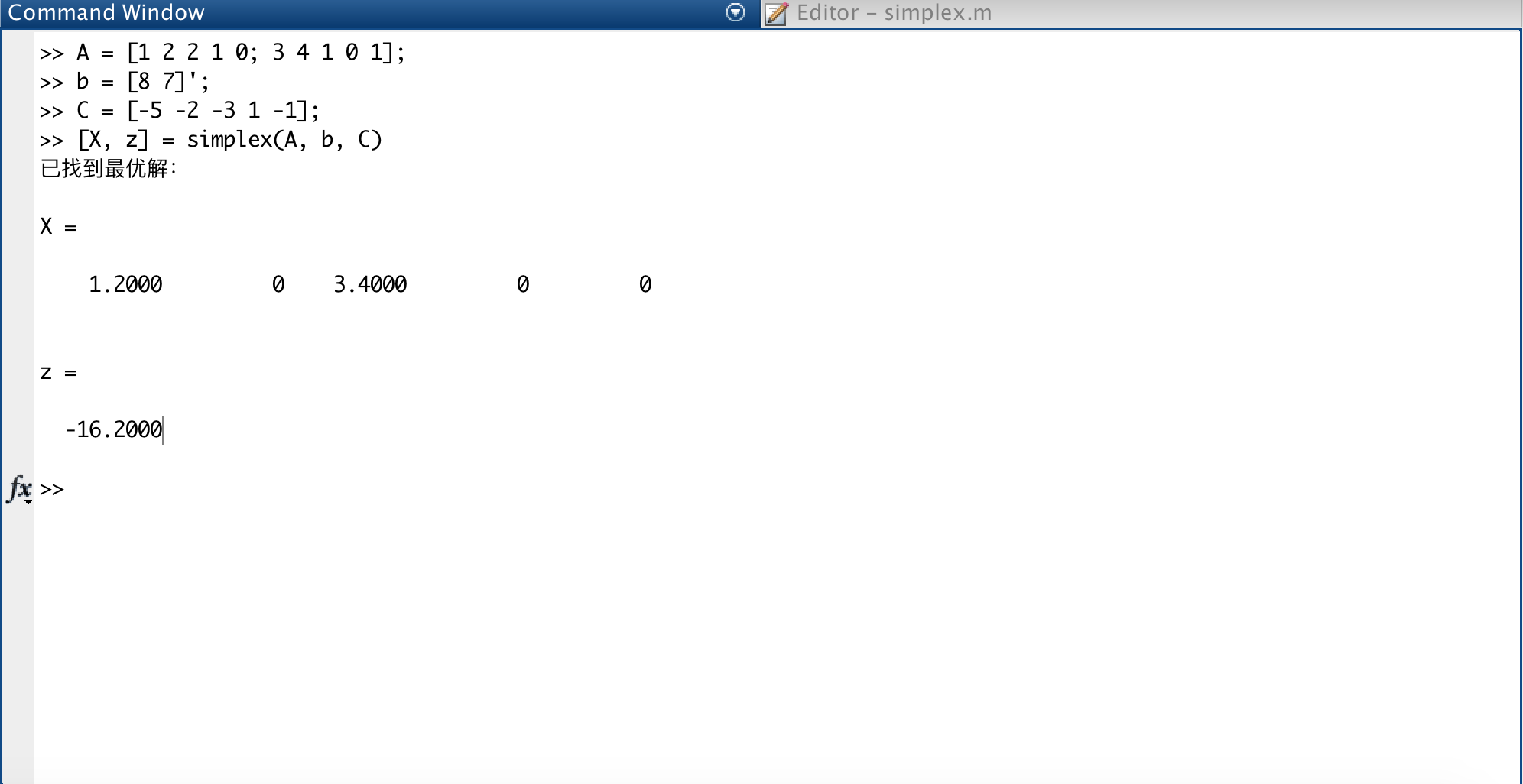
对于单纯形法中的例子，求解如下：