494.目标和

题目描述：

给定一个非负整数数组，a1, a2, ..., an, 和一个目标数，S。现在你有两个符号 + 和 -。对于数组中的任意一个整数，你都可以从 + 或 -中选择一个符号添加在前面。

返回可以使最终数组和为目标数 S 的所有添加符号的方法数。

示例 1:

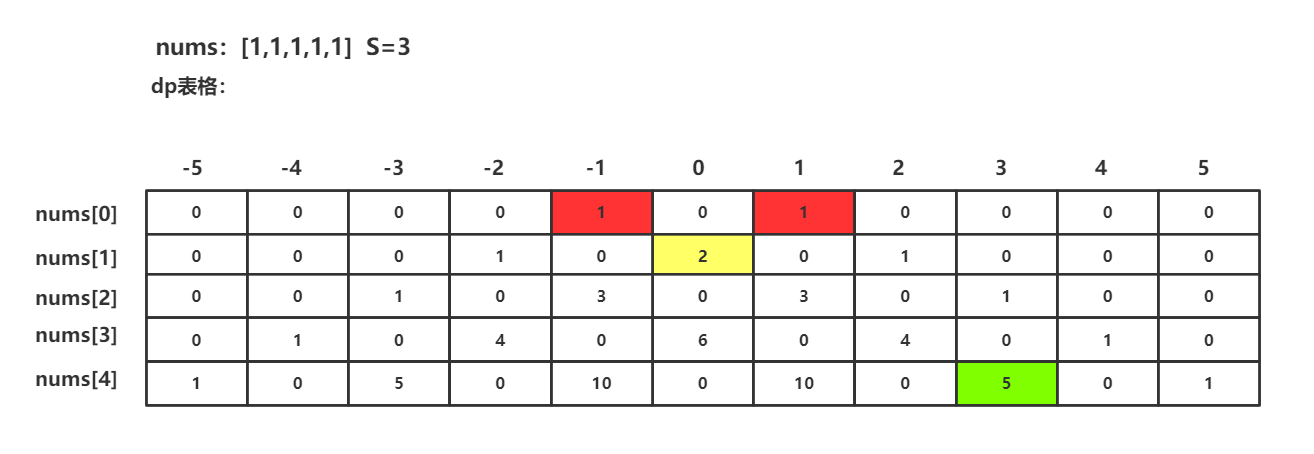
输入: nums: [1, 1, 1, 1, 1], S: 3
输出: 5
解释:

-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3

一共有5种方法让最终目标和为3。
注意:

数组非空，且长度不会超过20。
初始的数组的和不会超过1000。
保证返回的最终结果能被32位整数存下。

 

思想：动态规划

借鉴0-1背包，使用dp[i][j]记录选用nums中0-i个数字，组成目标为j时的方法数。

状态转移方程为：dp[i][j] = dp[i-1][j-nums[i] + dp[i-1][j+nums[i]

下表为dp[len][t]的表格，其中len=nums.size(),t=2*sum+1(sum为nums中所有元素的和),绿色表格为最终所求的方法数。

详情参考：https://leetcode-cn.com/problems/target-sum/solution/dong-tai-gui-hua-si-kao-quan-guo-cheng-by-keepal/

代码：

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int S) {
        int sum = 0;
        for(int i=0;i<nums.size();i++)
            sum += nums[i];
        if(abs(S) > abs(sum))
            return 0;
        int t = sum * 2 + 1; //注意t的取值
        int len = nums.size();
        vector<vector<int>> dp(len,vector<int>(t));
        if(nums[0] == 0)
            dp[0][sum] = 2;
        else{
            dp[0][sum + nums[0]] = 1;
            dp[0][sum - nums[0]] = 1;
        }
        for(int i = 1;i < nums.size();i++)
            for(int j = 0;j < t;j++){
                int l = (j - nums[i]) >= 0 ? j-nums[i] : 0;
                int r = (j + nums[i]) < t ? j+nums[i] : 0;
                dp[i][j] = dp[i-1][l] + dp[i-1][r];
            }
        return dp[nums.size()-1][sum + S];
    }
};

注意：当nums[0]=0时，dp[0][sum]需要初始化为2，因为加减0都得0