279. 完全平方数

题目描述：

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

示例 1:

输入: n = 12
输出: 3
解释: 12 = 4 + 4 + 4.
示例 2:

输入: n = 13
输出: 2
解释: 13 = 4 + 9.

 

思想：动态规划

解决递归中堆栈溢出的问题的一个思路就是使用动态规划（DP）技术，该技术建立在重用中间解的结果来计算终解的思想之上。

要计算 numSquares(n) 的值，首先要计算 n之前的所有值，即 numSquares(n-k)  )∀k∈square numbers。

如果已经在某个地方保留了数字 n-k 的解，那么就不需要使用递归计算。

几乎所有的动态规划解决方案，首先会创建一个一维或多维数组 DP 来保存中间子解的值，以及通常数组最后一个值代表最终解。注意，创建了一个虚构的元素 dp[0]=0 来简化逻辑，这有助于在在余数 (n-k）恰好是一个完全平方数的情况下。
还需要预计算小于给定数字 n 的完全平方数列表（即 square_nums）。
在主要步骤中，从数字 1 循环到 n，计算每个数字 i 的解（即 numSquares(i)）。每次迭代中，将 numSquares(i) 的结果保存在 dp[i] 中。
在循环结束时，返回数组中的最后一个元素作为解决方案的结果。
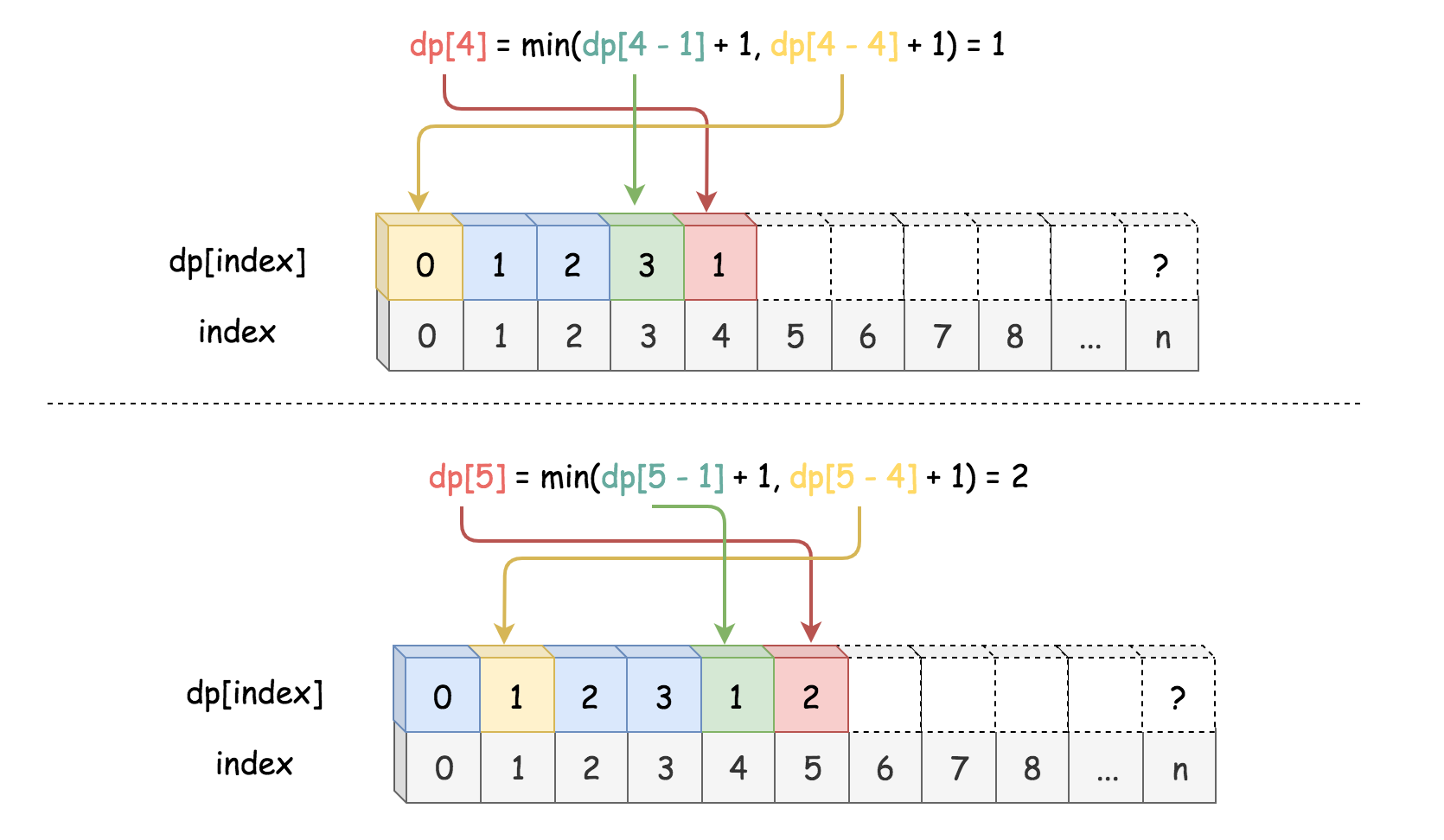
在下图中，演示了如何计算与 dp[4] 和 dp[5] 相对应的 numSquares(4) 和 numSquares(5) 的结果。

 

参考：

https://leetcode-cn.com/problems/perfect-squares/solution/wan-quan-ping-fang-shu-by-leetcode/

代码：

class Solution {
public:
    int numSquares(int n) {
        vector<int> dp(n+1,INT_MAX);
        vector<int> square(n+1);
        for(int i=0;i<n+1;i++)
            square[i] = i * i;
        dp[0] = 0;
        for(int i=1;i<n+1;i++){
            for(int j=1;j<n+1;j++){
                if(i<square[j])
                    break;
                dp[i] = min(dp[i],dp[i-square[j]]+1);
            }
        }
        return dp[n];
    }
};