221. 最大正方形

 

题目描述：

在一个由 0 和 1 组成的二维矩阵内，找到只包含 1 的最大正方形，并返回其面积。

示例:

输入:

1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0

输出: 4

 

思想：动态规划

• 若形成正方形（非单 1），以当前为右下角的视角看，则需要：当前格、上、左、左上都是 1
• 可以换个角度：当前格、上、左、左上都不能受 0 的限制，才能成为正方形

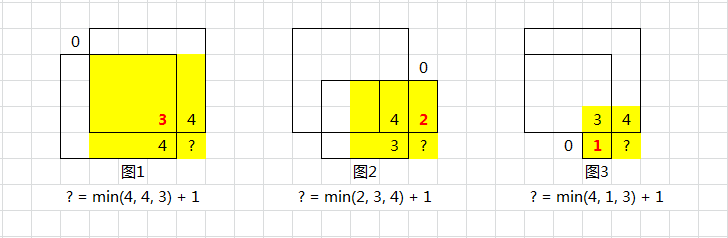
• 图1：受限于左上的0
• 图2：受限于上边的0
• 图3：受限于左边的0
• 数字表示：以此为正方形右下角的最大边长
• 黄色表示：格子 ? 作为右下角的正方形区域

参考：

https://leetcode-cn.com/problems/maximal-square/solution/li-jie-san-zhe-qu-zui-xiao-1-by-lzhlyle/

 

代码：

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        if(matrix.size()==0||matrix[0].size()==0)
            return 0;
        int height = matrix.size();
        int width = matrix[0].size();
        int maxSide = 0;
        vector<vector<int> > dp(height+1,vector<int>(width+1,0));  
　　　　//预先设定dp的第一行和第一列都是0，dp[1][1]对应matrix[0][0]的最大正方形边长
        for(int i=0;i<height;i++)
            for(int j=0;j<width;j++){
                if(matrix[i][j]=='1')
                    dp[i+1][j+1] = min(min(dp[i][j],dp[i+1][j]),dp[i][j+1])+1;
                    maxSide = max(maxSide,dp[i+1][j+1]);
            }
        return maxSide * maxSide;
    }
};

注：

用vector创建二维向量(元素均为0)：

vector<vector<int> > dp(m,vector<int>(n,0))