62. 不同路径

题目描述：

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

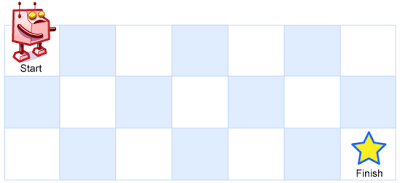
例如，上图是一个7 x 3 的网格。有多少可能的路径？

 

示例 1:

输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右
示例 2:

输入: m = 7, n = 3
输出: 28
 

提示：

1 <= m, n <= 100
题目数据保证答案小于等于 2 * 10 ^ 9

 

思想：

递归，先确定递归出口，然后执行递归操作

注：在执行递归过程中可以吧经过的路线用数组保存，不然会超时（因为有很多重复计算）

 

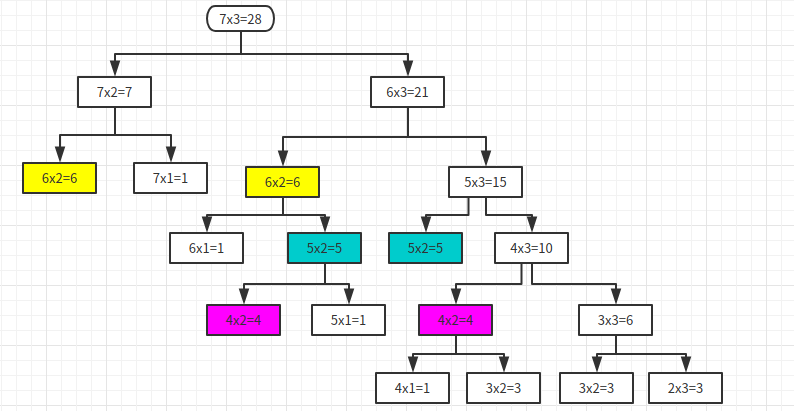
代码：

static int a[101][101]={0};  //记录已经计算过的路径，大大提高效率
class Solution {
public:
    int uniquePaths(int m, int n) {
        if(m<=0 or n<=0)
            return 0;
        else if(m==1 || n==1)
            return 1;
        else if(m==2 && n==2)
            return 2;
        else if((m==2&&n==3) || (m==3&&n==2))
            return 3;
        if(a[m][n]>0)
            return a[m][n];
        a[m][n-1] = uniquePaths(m,n-1);
        a[m-1][n] = uniquePaths(m-1,n);
        a[m][n] = a[m][n-1] + a[m-1][n];
        return a[m][n];
    }
};