贪心构造题目
CF83C
枚举可能的 \(26^{4}\)种经过的集合方案,算一下到(n,m)的可达性,然后从(1,1)开始贪心即可。
CF1738F
每次找一个度数最大的点,遍历所有出边,如果邻居被遍历过,那么把当前集合加入邻居的集合,否则把邻居加入当前集合。
(这个真的有2400吗)
CF1208F
这种只有位运算的题第一反应是高位贪心,考虑枚举i,那么要最大化的就是 \(a_{i}\) 中为0的位在序列右边的贡献,某一位有贡献仅当 \(a_{j}\) 和 \(a_{k}\) 都有这一位。那么对 \(a_{i}\) 中为0的位高位贪心即可。“若干位为给定值的限制”相当于高维后缀次大。预处理高维后缀最大和次大即可。
CF796F
考虑限制1相当于每个点有一个上限,与此同时还要求某个区间里至少某一个数出现过1次。先处理每个点的上限,发现只要每种上限的所有位置中至少有一个值取到上限即可满足题意,因为一种上限一定恰好来自于一个区间。要求或最大,如果有至少2个数无上限,那么构造 \(2^{29},2^{29}-1\) 即可。否则对于每种限制,如果只有一个数则构造上限,如果有两个数则构造{上限,\(2^{\lfloor\log 上限\rfloor}-1\)}。构造完之后如果有无限制的数,那么填补对应位即可。
没做出来是因为没看到x互不相同的限制,不知道其实“某个区间里至少某一个数出现过1次”就等价于每种限制必须有一个数取到上界。
注意维护上限的时候显然不用写beats,而是把区间取min标记永久化。
CF1174F
被创死了。
考虑如何高效地缩减范围。假设当前已经知道x只能在u子树里,那么对于u开头的重链,我们可以使用一次d操作询问处重链上最深的是x祖先的点,然后用一步s操作找到下一个祖先。这样会使子树规模缩小一半。
CF232C
题解没看懂,寄。
CF1477D
CF1592E
发现奇数长度区间一定不合法,偶数长度区间只要保证比区间与最高位高的位异或和是0即可。异或和是0转化成前缀异或和相等判断即可。
CF1159F
CF1182D
总是考虑将两维分离考虑,枚举每个点最终成为那个角,尝试找到正方形(x,y,a)使得曼哈顿距离之和最小。不考虑正方形的限制,最优解显然是所有边界在对应两点之间。在有限制的情况下可以先求出横纵坐标对应边长取值范围,无交则让一个迁就另一个。
CF1375G
两种做法:
1.给树黑白染色之后发现每次恰好某种颜色数量-1,终态是一黑若干白,那么操作次数就是min(黑个数,白个数)-1。
2.树上换根dp,枚举最后菊花的根,那么答案就是该点吊起来当根之后孙子节点的个数+各孙子子树内收束到孙子的答案。(此做法正确性存疑)
CF1059E
从底下贪心的往上填。如果子树里还有可以向上延伸的就向上延伸,否则新开一个链。
CF1697E
感性理解大量的点之间是不能同色的。首先考虑如果两个点颜色相同意味着什么,根据题目的要求可以算出一个可行点集,这个点集可以同时染成同一种颜色。可以推得可行点集之间是无交的,证明是考虑交集中的点,无论怎么样都不合法。然后手玩一下可以发现其实可行点集最大只能是4。所以枚举2,3,4各选择了多少个简单排列组合即可。
CF30D
考虑什么时候经过特殊的n+1号点。之前一定是走了一个前缀或者后缀,枚举这个前后缀即可。
CF1391E
构造很有道理但是怎么想到呢。
如果dfs树深度大于一半则做任务1。
否则dfs树上每层选点对直到剩下不超过一个点即可。
CF1793E
记得这题当时场上没想明白来着。
对a排序,发现答案一定是前缀。考虑确定答案范围情况下最多可以安排多少本书,这个可以在前缀上递推。因为答案有单调性所以二分/从小到大枚举都能完成此题。
P5479 IOI2019 排列鞋子
可以很轻松的确定一双鞋子最后会到哪里去,因为相同大小的相同类型鞋子在最优解中不会交换,把对应关系排列建出来就转化成数逆序对。
CF1819C
结论是只有毛毛虫可以构造。找毛毛虫就是找直径然后判断其他点到直径的距离是不是都是1。
毛毛虫的证明直接复制洛谷题解区,来自洛谷用户 plank_black ,感谢:
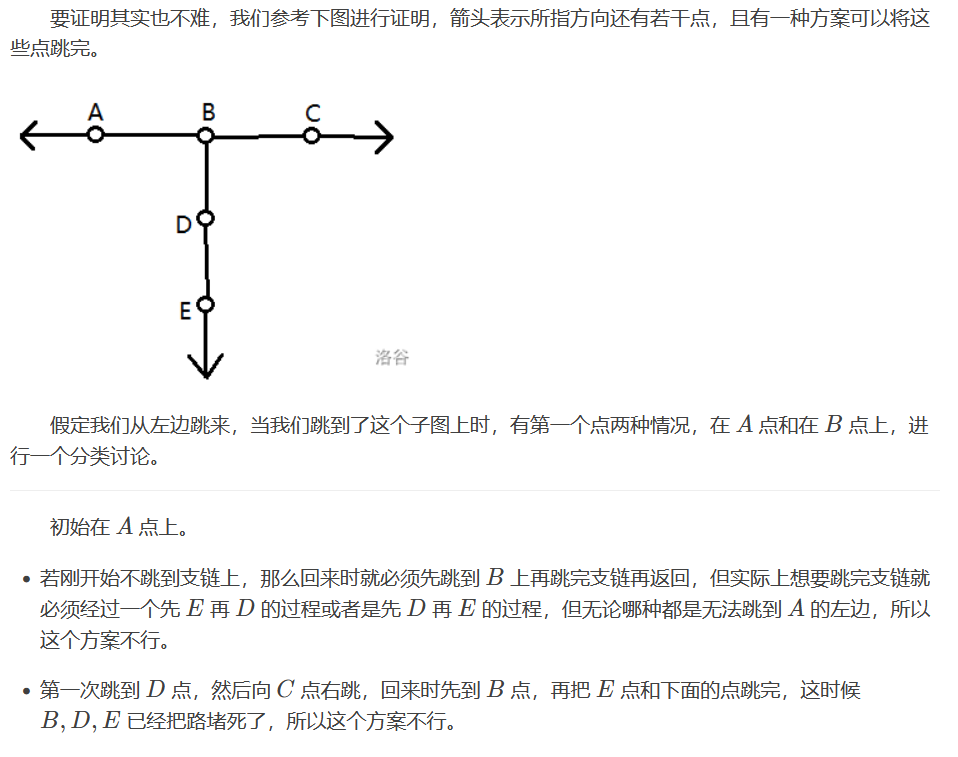

CF10D
虽然很有道理但是有点难接受,总感觉有点神奇。
先考虑3方暴力:
图中内容来自洛谷用户 李若谷 ,感谢:

考虑平方:枚举 \(k\) 是可以避免的,因为每次找的都是下标小于 \(j\),值小于 \(a_{i}\) 的 \(f_{i,k}\) 的最小值。j和j+1只差了一个元素,维护这个每次只增加1个元素的集合即可。
CF1654F
设f(x,k)表示异或x后的前 \(2^{k}\) 位。注意到$$f(x,k)=f(x,k-1)+f(x xor 2^{k-1},k-1)$$。这个很像后缀排序,直接用后缀排序的思想做即可。内层用sort是 \(n^{2}2^{n}\) 的,用基数排序是 \(n2^{n}\) 的,均可以通过。
CF1163E
很快就想到了答案应该是线性基的填满的最大前缀和格雷码的构造。证明是首先数列中任意两个元素的异或和一定是S构成的线性空间中的数,又因为数列里有0,所以各个元素也是S构成的线性空间中的数。
CF1599A
CF1753D
先感性理解一个梯子一定不会移到一个和初始位置完全不重合的位置,因为这意味着要先把目标位置腾空,然后移过去。但是目标位置已经腾空的话直接放新梯子就好了,挪过去是多余的。然后把一个梯子的移动看成一个空地的移动,相当于把两个空地移到两个相邻的位置,多源最短路即可。
CF1042F
树上贪心,考虑子树中每个向上传的集合的最大深度,最优解就是把小的合起来,把大的直接单另出来开一个新集合。
CF1612F
一个很显然的构造方式是先倍增构造小的然后构造大的。这启发我们答案不会很大(不超过 \(\log n+\frac{m}{n}\)),对每一步维护 \(f_{i}\) 表示A为i时最大的B。除开最后一步之外,一定是合最大,这样状态数 \(n\times ans\),转移 \(O(1)\)。最后枚举倒数第二步走到哪即可。
CF1656F
首先 \(f\) 关于 \(t\) 是凸的,因为每一棵生成树关于 \(t\) 都是一条直线。直线集合取min显然是下凸的。考虑对于固定的 \(t\) 咋求,根据prim算法,最优解是 \(a_{1}\) 和 \(a_{n}\) 连,其他点向和自己异号的端点连边。
cf1866I
首先发现这是一个公平游戏,而且不涉及局面的和,那么从必胜/必败的角度去考虑。
SG值一行只会有一个0,因为考虑本行的最后一个0,前面全部是非0(这个0是更前面的后继状态),根据假设,后面也全是非0。倒着枚举行,那么这一行的唯一一个可能的0的的位置就是没有被其他0占用的列中最靠右的。如果这个位置之后有特殊格子则这一行没有0。
CF1918G
构造题的经典思考方向是增量构造和循环构造。考虑增量构造,对于一个合法的序列,设其为 [....a,b]。那么发现 [....a,b,-a,a-b] 是一个合法的解。那么只需要对奇数和偶数找到最小的合法解。
CF1919f2
两种做法:
1
线段树维护四个信息:
- 区间答案
- 区间还有多少可以转化成酒的空间
- 区间全部被填满之后还有多少水可以到右端点前往下一个区间
- 区间现在在右端点的水量
四个信息的合并看代码不难理解。
2
看成最大流问题,转化成最小割,发现 \(a_{i}\) 和 \(b_{i}\) 一定恰好割掉一个,记录区间开头结尾割掉的是哪种,转移的时候如果左边割掉a,右边割掉b,那么需要额外割掉中间的c。
CF1817D
先考虑目标块x在左半边怎么做。发现可以一直RDRU,直到x在第一行的最左边,再来一次L。
x在正中间平凡。
x在右半边时可以执行镜像的上一种操作直至x来到右上角。然后再执行原本的上一种操作来让所有块来到右半边,然后LDRU。这样x就会来到(n-1)/2的位置。
CF1920F
类似于计算几何中求一个点是否在一个图多边形内,从岛屿向地图边缘连一条线,要求路径必须经过这条线奇数次之后回到自身。然后对每个点建奇点和偶点,题目就等价于最大的x使得只保留 \(\geq x\) 的点,存在一对奇偶点联通。这就是经典的点权重构树,具体实现的时候实现成边权重构树即可。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号