2019ICPC银川C

先考虑暴力dp：设 \(dp_{i}\) 表示前 \(i\) 个的最小划分代价。

\[dp_{i}=min_{1\leq j\leq i-k}max(dp_{j},diff[j+1,i]) \]

然后如果把 \(dp_{j}\) 换成 \(min(dp[j,i-k])\)，这个式子仍然是正确的，因为对于 \(l\in [j+1,i-k]\)，\(max(dp_{l},diff[j+1,i]) \geq max(dp_{l},diff[l+1,i])\)（\(diff[a,b]\) 对于固定的 \(b\) 随着 \(a\) 减小单调不降）。相当于添加了一些显然不优的决策。

这样dp式就变成

\[dp_{i}=min_{1\leq j\leq i-k}max(min(dp[j,i-k]),diff[j+1,i]) \]

对于固定的右端点 \(i\)，考虑所有 \(j\) 的 \(min(dp[j,i-k])\) 和 \(diff[j+1,i]\)。不难发现，随着 \(j\) 的左移，一个单调不降一个单调不升。要求的是两者max的min，那就是求圈出来的部分的最小值，显然只可能在拐点前后。

再考虑 \(i\) 到 \(i+1\) 的过程，dp折线上的每个点只能下降或不变，diff折线上的每个点只能上升或不变，这启发我们拐点只会朝右走（这个直观上来理解就是剪刀剪东西由开到合的时候两边重合的临界点只会往右走），是单调的。维护拐点 \(head\) 和 \(diff[head+1,i]\)，\(dp[head,i-K]\)。因为每次 \(head\) 和 \(i\) 只变化1，所以可以用莫队的方式维护，只要用一个数据结构维护插入，删除，查询最大/最小值，multiset可以胜任。

这张图或许能帮助你更好地理解。

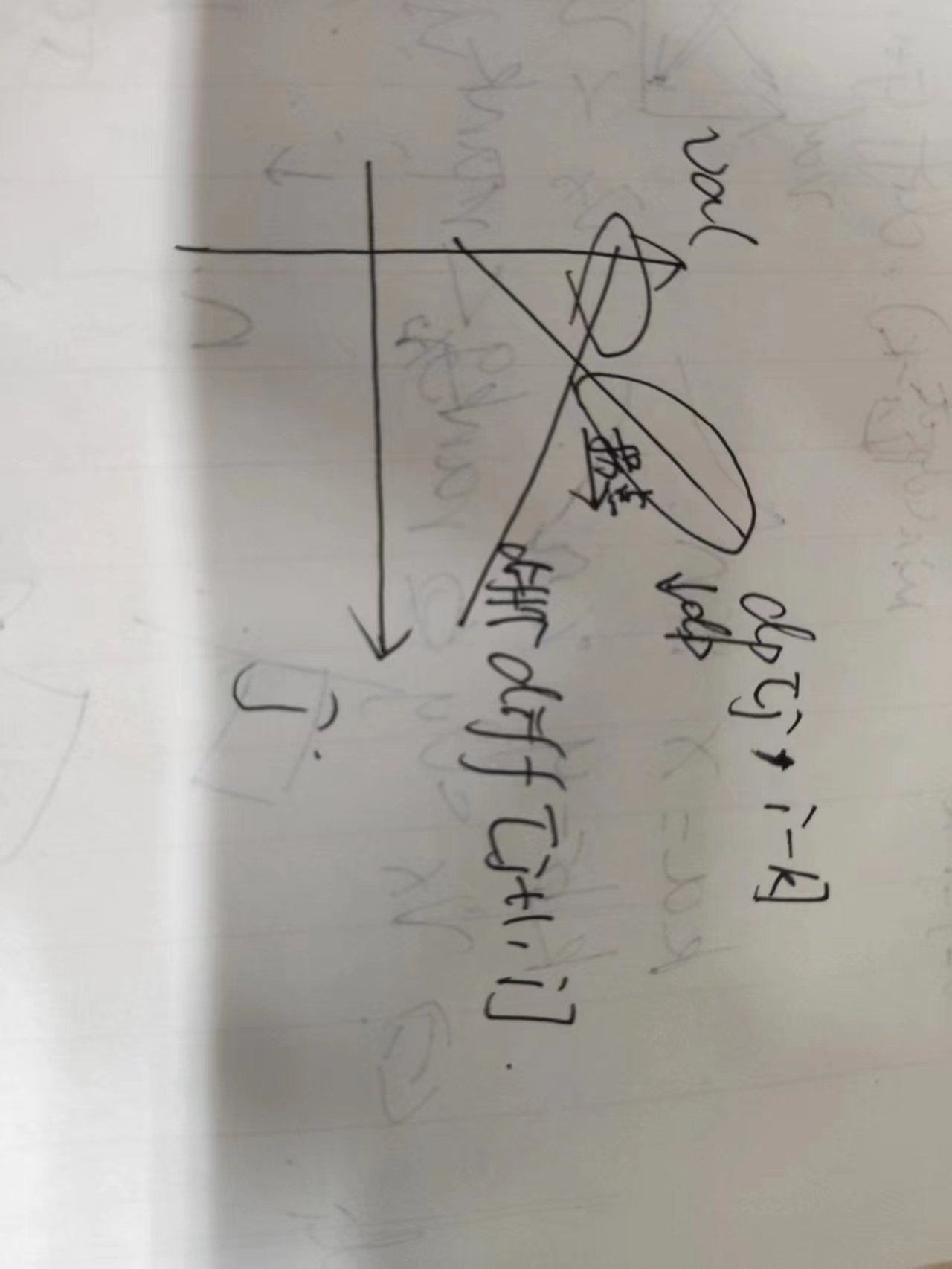
复杂度一个log，题解好像有高论线性做法，我不会。

代码无法在cf上通过，在qoj上能通过但不稳定，卡着时限过的。

update at 2023/11/4：[head,i]的区间a最大值，a最小值，dp最小值可以用单调队列维护。懒得再写一遍了。

#pragma GCC optimize("O3")
#include<bits/stdc++.h>
using namespace std;
const int INF=2147483647;
const int N=1e6+5;
int n,K,last_ans,head(0),now_dp,now_diff,a[N],dp[N],pre_dp,pre_diff;
multiset<int> S_of_dp,S_of_diff;
int max(int a,int b) {
	return a>=b?a:b;
}
int min(int a,int b) {
	return a<=b?a:b;
}
void add_dp(int x) {
	S_of_dp.insert(x);
	now_dp=*S_of_dp.begin();
}
void del_dp(int x) {
	S_of_dp.erase(S_of_dp.find(x));
	now_dp=*S_of_dp.begin();
}
void add_diff(int x) {
	S_of_diff.insert(x);
	now_diff=(*S_of_diff.rbegin())-(*S_of_diff.begin());
}
void del_diff(int x) {
	S_of_diff.erase(S_of_diff.find(x));
	now_diff=(*S_of_diff.rbegin())-(*S_of_diff.begin());
}
void get_pre_dp_diff(int pos) {
	if(pos!=0) {
		pre_dp=min(now_dp,dp[pos-1]);
		pre_diff=max(*S_of_diff.rbegin(),a[pos])-min(*S_of_diff.begin(),a[pos]);
	} else {
		pre_dp=pre_diff=INF;
	}
	return;
}
void put(int x) {
	if(x>9)put(x/10);
	putchar((char)(x%10+'0'));
}
int read() {
	int x(0);
	char ch(getchar());
	while(ch>'9'||ch<'0')ch=getchar();
	while(ch<='9'&&ch>='0') {
		x=x*10+ch-'0';
		ch=getchar();
	}
	return x;
}
int main() {
	n=read();
	K=read();
	for(int i=1; i<=n; i++) {
		a[i]=read();
		a[i]^=last_ans;
		add_diff(a[i]);
		if(i>=K) {
			add_dp(dp[i-K]);
			while(now_diff>=now_dp&&head<i-K) {
				del_diff(a[head+1]);
				del_dp(dp[head]);
				head++;
			}
			get_pre_dp_diff(head);
			last_ans=dp[i]=min(max(now_dp,now_diff),max(pre_dp,pre_diff));
		} else {
			dp[i]=INF;
			last_ans=0;
		}
		put(last_ans);
		putchar('\n');
	}
	return 0;
}