PAM+回文串border理论

PAM板子

#include <bits/stdc++.h>
using namespace std;
const int maxn = 300000 + 5;

namespace pam {
	int sz, tot, last;
	int cnt[maxn], ch[maxn][26], len[maxn], fail[maxn];
	char s[maxn];

	int node(int l) {  // 建立一个新节点，长度为 l
		sz++;
		memset(ch[sz], 0, sizeof(ch[sz]));
		len[sz] = l;
		fail[sz] = cnt[sz] = 0;
		return sz;
	}

	void clear() {  // 初始化
		sz = -1;
		last = 0;
		s[tot = 0] = '$';
		node(0);
		node(-1);
		fail[0] = 1;
	}

	int getfail(int x) {  // 找后缀回文
		while (s[tot - len[x] - 1] != s[tot]) x = fail[x];
		return x;
	}

	void insert(char c) {  // 建树
		s[++tot] = c;
		int now = getfail(last);
		if (!ch[now][c - 'a']) {
			int x = node(len[now] + 2);
			fail[x] = ch[getfail(fail[now])][c - 'a'];
			ch[now][c - 'a'] = x;
		}
		last = ch[now][c - 'a'];
		cnt[last]++;
	}

	long long solve() {
		long long ans = 0;
		for (int i = sz; i >= 0; i--) {
			cnt[fail[i]] += cnt[i];
		}
		for (int i = 1; i <= sz; i++) {  // 更新答案
			ans = max(ans, 1ll * len[i] * cnt[i]);
		}
		return ans;
	}
}  // namespace pam

char s[maxn];

int main() {
	pam::clear();
	scanf("%s", s + 1);
	for (int i = 1; s[i]; i++) {
		pam::insert(s[i]);
	}
	printf("%lld\n", pam::solve());
	return 0;
}

回文串border理论

最小回文划分

• t是s的border，当且仅当|s|-|t|是s的周期。

• t是回文串s的后缀，t是s的border当且仅当t是回文串。

• t是回文串s的border(\(|s|\le 2|t|\))，s是回文串当且仅当t是回文串。

• t是回文串s的border，则|s|-|t|是s的周期，|s|-|t|为s的最小周期，当且仅当t是s的最长回文真后缀。

• x是一个回文串，y是x的最长回文真后缀，z是y的最长回文真后缀。令u,v分别为满足x=uy,y=vz的字符串，则有下面三条性质

  • |u| \(\ge\) |v|

  • 如果|u| > |v| ，那么|u| > |z|

  • 如果|u| = |v|，那么u=v。

• s的所有回文后缀按照长度排序后，可以划分成 \(\log |s|\) 段等差数列。

优化

回文树上的每个节点 \(u\) 需要多维护两个信息，\(diff[u]\) 和 \(slink[u]\)。\(diff[u]\) 表示节点 \(u\) 和 \(fail[u]\) 所代表的回文串的长度差，即 \(len[u]-len[fail[u]]\)。\(slink[u]\) 表示 \(u\) 一直沿着 fail 向上跳到第一个节点 \(v\)，使得 \(diff[v] \neq diff[u]\)，也就是 \(u\) 所在等差数列中长度最小的那个节点。

根据上面证明的结论，如果使用 \(slink\) 指针向上跳的话，每向后填加一个字符，只需要向上跳 \(O(\log |s|)\) 次。因此，可以考虑将一个等差数列表示的所有回文串的 \(dp\) 值之和（在原问题中指 \(\min\)），记录到最长的那一个回文串对应节点上。

\(g[v]\) 表示 \(v\) 所在等差数列的 \(dp\) 值之和，且 \(v\) 是这个等差数列中长度最长的节点，则 \(g[v]=\sum_{slink[x]=slink[v]} dp[i-len[x]]\)，这里 \(i\) 是当前枚举到的下标。

下面我们考虑如何更新 \(g\) 数组和 \(dp\) 数组。以下图为例，假设当前枚举到第 \(i\) 个字符，回文树上对应节点为 \(x\)。\(g[x]\) 为橙色三个位置的 \(dp\) 值之和（最短的回文串 \(slink[x]\) 算在下一个等差数列中）。\(fail[x]\) 上一次出现位置是 \(i-diff[x]\)（在 \(i-diff[x]\) 处结束），\(g[fail[x]]\) 包含的 \(dp\) 值是蓝色位置。因此，\(g[x]\) 实际上等于 \(g[fail[x]]\) 和多出来一个位置的 \(dp\) 值之和，多出来的位置是 \(i-(len[slink[x]]+diff[x])\)。最后再用 \(g[x]\) 去更新 \(dp[i]\)，这部分等差数列的贡献就计算完毕了，不断跳 \(slink[x]\)，重复这个过程即可。具体实现方式可参考例题代码。

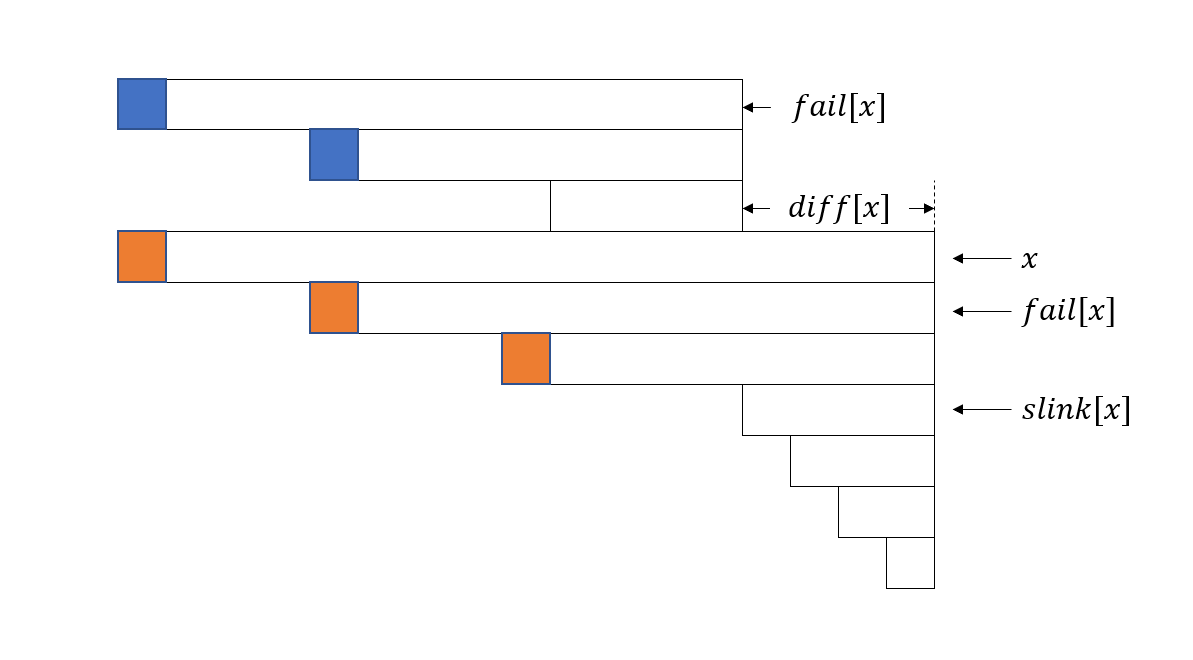
最后，上述做法的正确性依赖于：如果 \(x\) 和 \(fail[x]\) 属于同一个等差数列，那么 \(fail[x]\) 上一次出现位置是 \(i-diff[x]\)。

证明:根据引理 \(1\)，\(fail[x]\) 是 \(x\) 的 border，因此其在 \(i-diff[x]\) 处出现。假设 \(fail[x]\) 在 \((i-diff[x],i)\) 中的 \(j\) 位置出现。由于 \(x\) 和 \(fail[x]\) 属于同一个等差数列，因此 \(2|fail[x]| \ge x\)。多余的 \(fail[x]\) 和 \(i-diff[x]\) 处的 \(fail[x]\) 有交集，记交集为 \(w\)，设串 \(u\) 满足 \(uw=fail[x]\)。用类似引理 \(1\) 的方式可以证明，\(w\) 是回文串，而 \(x\) 的前缀 \(s[i-len[x]+1..j]=uwu\) 也是回文串，这与 \(fail[x]\) 是 \(x\) 的最长回文前缀（后缀）矛盾。

例题：Codeforces 932G Palindrome Partition

给定一个字符串 \(s\)，要求将 \(s\) 划分为 \(t_1, t_2, \dots, t_k\)，其中 \(k\) 是偶数，且 \(t_i=t_{k-i+1}\)，求这样的划分方案数。

题解:构造字符串 \(t= s[0]s[n - 1]s[1]s[n - 2]s[2]s[n - 3] \dots s[n / 2 - 1]s[n / 2]\)，问题等价于求 \(t\) 的偶回文划分方案数，把上面的转移方程改成求和形式并且只在偶数位置更新 \(dp\) 数组即可。时间复杂度 \(O(n \log n)\)，空间复杂度 \(O(n)\)。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int maxn = 1000000 + 5;

int add(int x, int y) {
	x += y;
	return x >= mod ? x -= mod : x;
}

namespace pam {
	int sz, tot, last;
	int ch[maxn][26], len[maxn], fail[maxn];
	int cnt[maxn], dep[maxn], dif[maxn], slink[maxn];
	char s[maxn];

	int node(int l) {  // 建立一个长度为 l 的新节点
		sz++;
		memset(ch[sz], 0, sizeof(ch[sz]));
		len[sz] = l;
		fail[sz] = 0;
		cnt[sz] = 0;
		dep[sz] = 0;
		return sz;
	}

	void clear() {  // 初始化
		sz = -1;
		last = 0;
		s[tot = 0] = '$';
		node(0);
		node(-1);
		fail[0] = 1;
	}

	int getfail(int x) {  // 找到后缀回文
		while (s[tot - len[x] - 1] != s[tot]) x = fail[x];
		return x;
	}

	void insert(char c) {  // 建树
		s[++tot] = c;
		int now = getfail(last);
		if (!ch[now][c - 'a']) {
			int x = node(len[now] + 2);
			fail[x] = ch[getfail(fail[now])][c - 'a'];
			dep[x] = dep[fail[x]] + 1;
			ch[now][c - 'a'] = x;
			dif[x] = len[x] - len[fail[x]];
			if (dif[x] == dif[fail[x]])
				slink[x] = slink[fail[x]];
			else
				slink[x] = fail[x];
		}
		last = ch[now][c - 'a'];
		cnt[last]++;
	}
}  // namespace pam

using pam::dif;
using pam::fail;
using pam::len;
using pam::slink;
int n, dp[maxn], g[maxn];
char s[maxn], t[maxn];

int main() {
	pam::clear();
	scanf("%s", s + 1);
	n = strlen(s + 1);
	for (int i = 1, j = 0; i <= n; i++) t[++j] = s[i], t[++j] = s[n - i + 1];
	dp[0] = 1;
	for (int i = 1; i <= n; i++) {
		pam::insert(t[i]);
		for (int x = pam::last; x > 1; x = slink[x]) {
			g[x] = dp[i - len[slink[x]] - dif[x]];
			if (dif[x] == dif[fail[x]]) g[x] = add(g[x], g[fail[x]]);
			if (i % 2 == 0) dp[i] = add(dp[i], g[x]);  // 在偶数位置更新 dp 数组
		}
	}
	printf("%d", dp[n]);
	return 0;
}