DP专题
UNR #2 积劳成疾 dp
把贡献剥离为每个数的每个数作为区间最大的次数次方的乘积。
考虑一个比较经典的套路,对于一个值域全部为[1,i-1]的序列,枚举第一个插入i的位置,那么,包含i的区间个数可以计算(已知左边数的个数和右边数的个数),就y有了这个dp柿子:
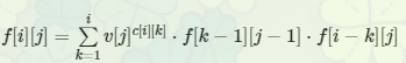 (copy自gxzlegend,特此注明出处)
(copy自gxzlegend,特此注明出处)
f[i][j]表示的是长度为i,值域为1-j的序列的权值和,c[i][k]表示长度为i的序列,覆盖下标k处的区间个数。
有一个边界情况,当i<K(这个K是题目给的K)时f[i][j]=序列个数=j^i.
UR #1 外星人
首先,有效的取模操作ai一定是单减的,所以先排个序,令dp[i][j]表示当前在第i位,当前值是j的序列方案输,枚举下一个转移的位置,就有:
\[dp[k][j mod ak]=dp[i][j]*A(minx[s[j]],minn[s[j]]-minn[s[j mod ak]]).
\]
解释一下为什么,考虑,我们当前选的模数是k,那么我们先把在 \((j \quad mod \quad a_{k},j]\) 之间的模数随意填,方案数就是那个dp[i][j]的系数,然后在最靠前的没有填的位置上填ak,再向后dp。
然后我们发现,在转移的时候,第二维的下标是单调递减的,所以我们可以省去第一位,只记录f[j],枚举一个比j小的模数ak,转移即可。(鬼想得到还可以这样优化!!!)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号