汇编代码优化入门&&数据流 CSapp第五章

 

汇编代码优化的局限性

　　对于：

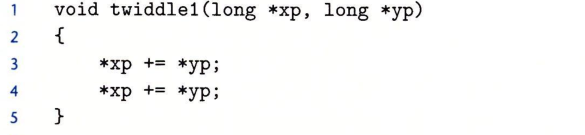
　　这样的一段代码，我们很容易想到优化成：

　　这样，然而这样优化是错误的，当且仅当xp和yp指向同一块内存单元。

消除不必要的内存引用

　　如下图，有这样一段代码：

　　我对于SSE指令集不太熟悉。这和普通的asm汇编还是有很大区别的。SSE指令集的全称是Streaming SIMD Extensions，课件这个指令集和SIMD有很大的关系。它是一种在MMX基础上发展出来的SIMD指令集，其不再占用浮点寄存器，而是使用单独的128位XMM寄存器。在此基础上又发展除了SSE2/SSE3/SSE4指令集。SSE2则进一步支持双精度浮点数，由于寄存器长度没有变长，所以只能支持２个双精度浮点计算或是４个单精度浮点计算，另外，它在这组寄存器上实现了整型计算，从而代替了MMX。SSE3支持一些更加复杂的算术计算。SSE4增加了更多指令，并且在数据搬移上下了一番工夫，支持不对齐的数据搬移，增加了super shuffle引擎等。

　　xmm0是SSE当中的128位寄存器。

　　可以看到，源数据的地址指针保存在%rbx寄存器当中，每次读取到%xmm0寄存器当中。

　　rdx是始终指向data[i]的，可以看到rdx在循环当中每次都会加8，也就是说数据大小位8字节，64位。

　　vmulsd   (%rdx)  ,%xmm0,%xmm0

　　这句代码是将data[i]乘以源数据的值，然后将中间结果保存到%xmm0当中。

　　下一句vmovsd %xmm0 ,(%rbx)将数据写回dst当中去。

 

　　可以看出这样的代码是十分冗余的，只需要这样：

　　就能够完成同样的功能。

重中之重——利用处理器微体系结构优化

　　经典的使代码适应机器。

　　数据流（data-flow）概念的引入：

　　然后我们就来学习一下如何从机器级代码得到数据流图：

　　如下图代码：

 

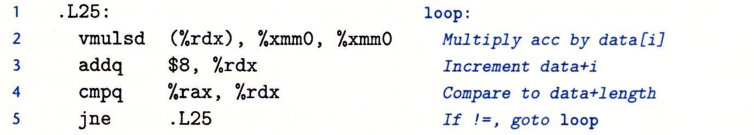
 　　数据流图为：

 

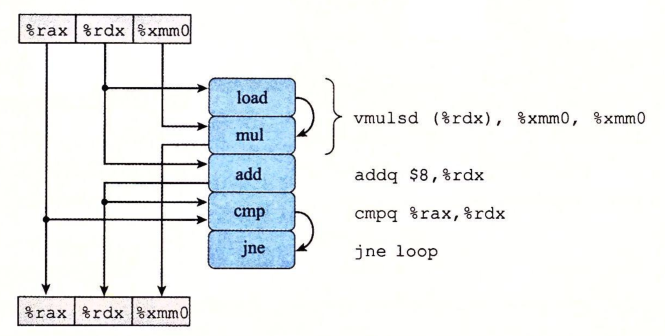
　　最上面是寄存器开始的值，最下面是寄存器结束之后的值。（%rdx）涉及到针对内存的读取，对应的是右边的load操作。

　　我们需要从这张图上发掘数据依赖关系。

　　

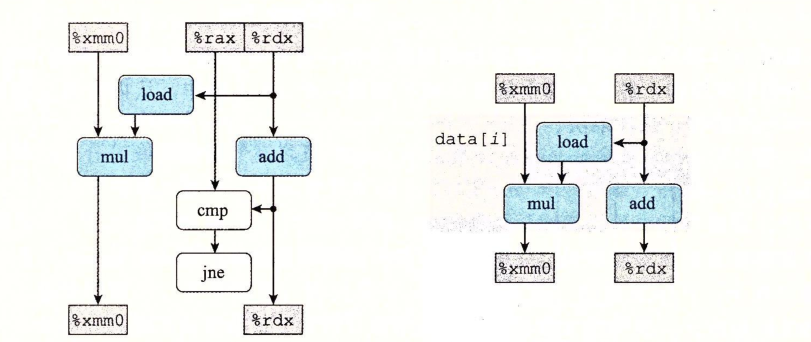
　　cmp和jne属于分支预测环节，假如采用分支预测技术，那么就可以假定这两个环节不影响。另外rax的值一直没有改变。

　　所以程序执行流程最终可以简化为：

　　

 

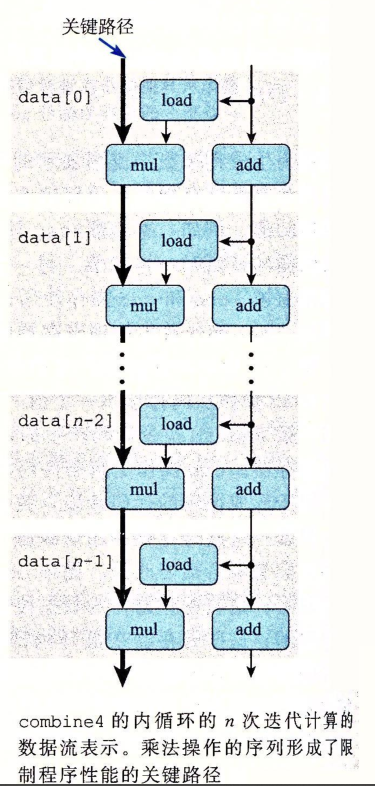
　　为什么乘法操作序列会成为关键路径呢？

循环展开

　　经典的优化方法。

　　利用数据流图我们可以更好地认识到循环展开是怎么优化的。

　　对于代码：

 

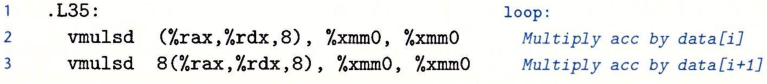
　　可以得到数据流图：

　　

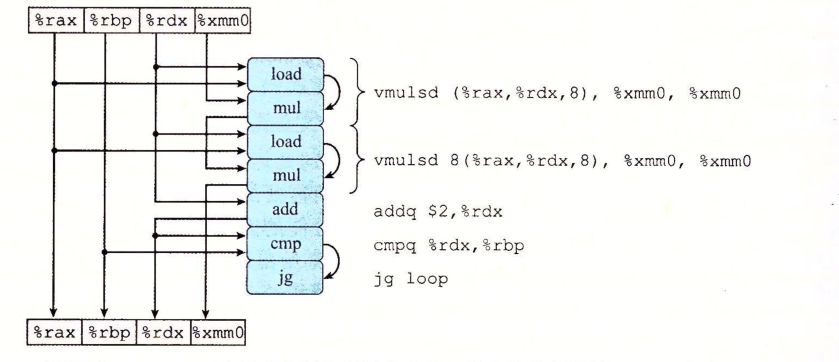
　　重新排列：

 

 

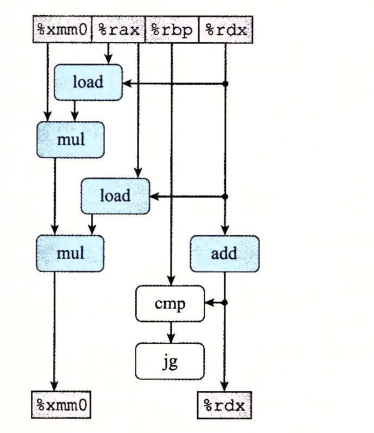
 　　最终获得：

 

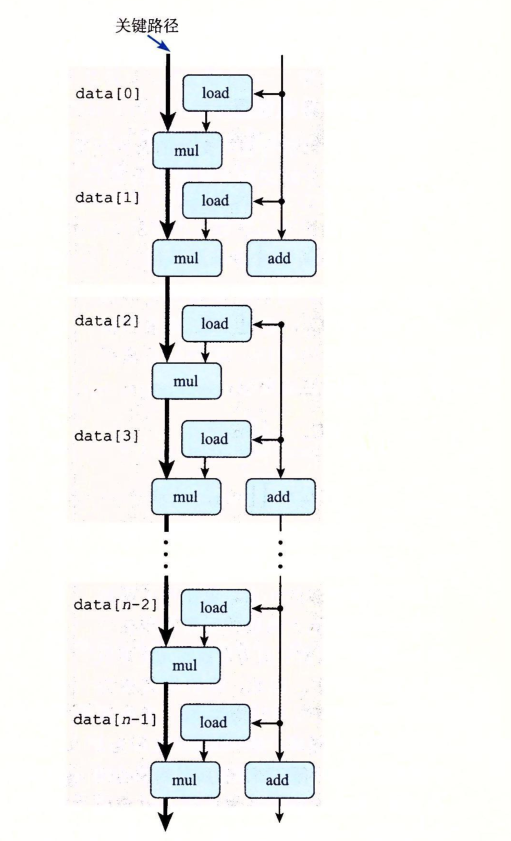
　　可以看出来，循环展开并没有优化乘法运算的性能。关键路径上任然是mul-load操作的密集排列。

　　书上的

 

　　这张图也说明了这一点。

 

提高并行----使用多个累积变量

　　观察前面的关键路径上的mul-load序列，我们尝试想一下：能不能在mul的时候load？

　　可以！再提供一个累积变量xmm1即可！

　　代码如下：

 

 

 

 

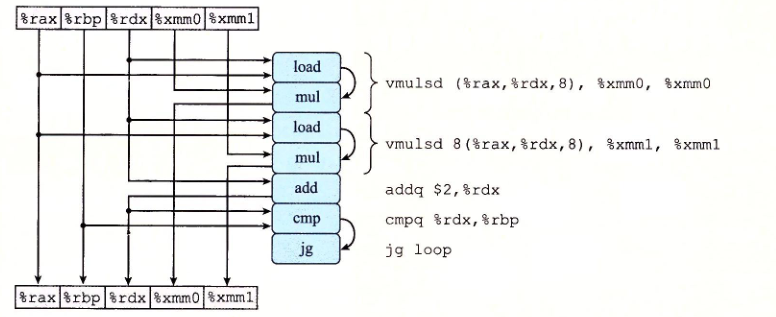
　　重新排列：

　　最终：

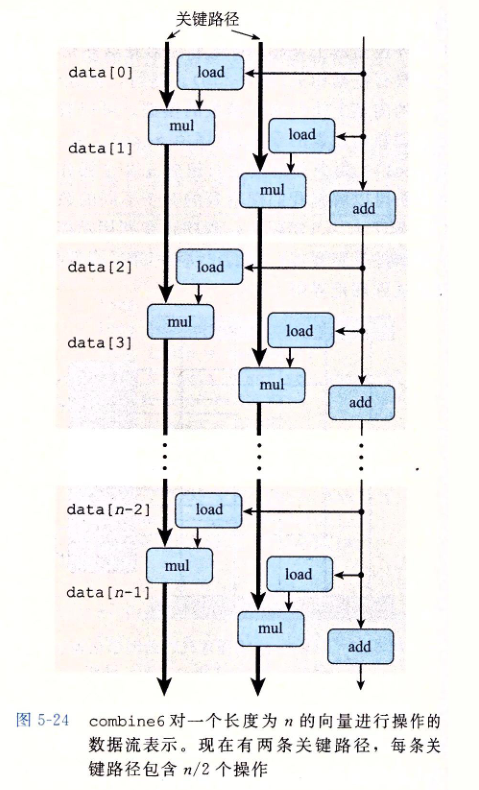
　　显然代码得到了优化。

重新结合变换

　　前面的运算其实就是累乘运算。

　　原本的结合顺序是：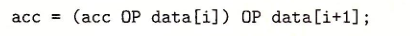

　　现在改变为：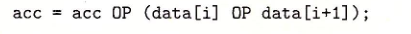

　　这就叫做重新结合变换。

　　

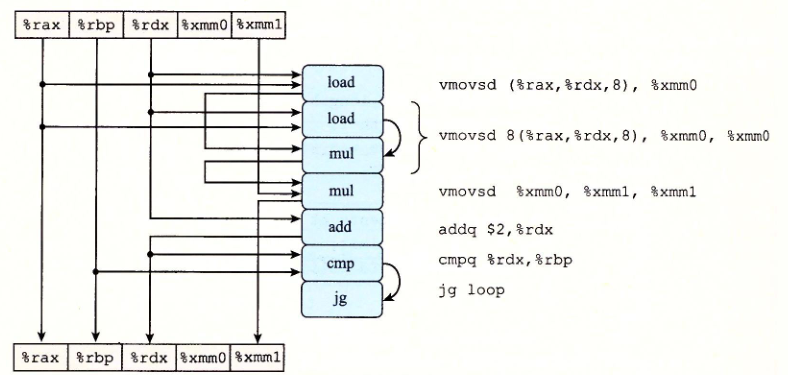
　　就是1*2*3*4*5*6*7*8=（1*2）*（3*4）*（5*6）*（7*8）  （遗憾的是不满足结合律的运算无法这样使用）

　　

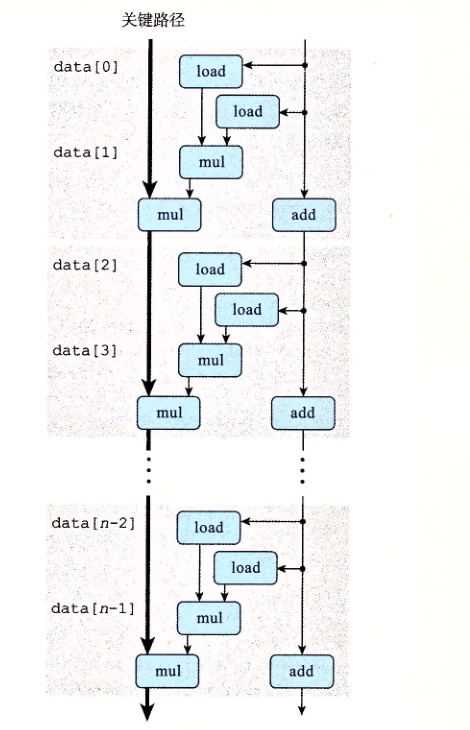
 课后作业5.13

　　

 

 

 

A：数据流图如下图所示：

      

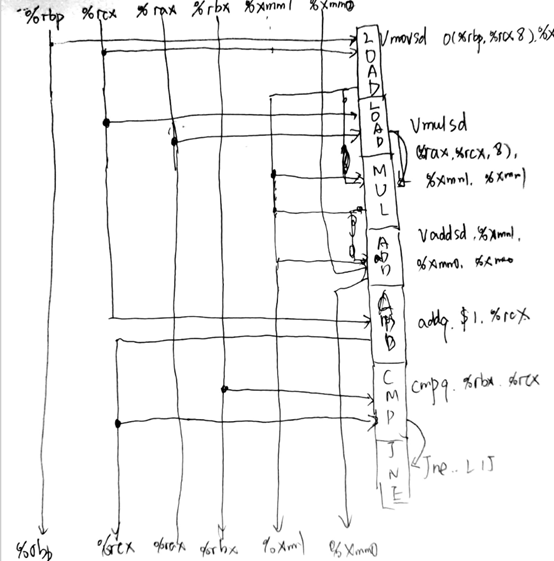
       形成关键路径：

 

 

 

B：

对于浮点数加法运算，CPE的下界为3

C：

对于整数加法运算，CPE运算的下界为1

D：

　　浮点数乘法在该数据流图当中，不存在数据依赖。因为在上图的这个算子当中，各个算子之间只有加法存在数据依赖，也就是下一个算子执行add运算之前，必须先得到前一个算子的add执行结果。

    但是对于浮点数乘法运算来说，各个算子当中的乘法运算都是不相关的，可以各自独立进行。故而运算CPE下界由3.0的浮点数加法运算决定。

 　　

　　我觉得一个关键路径就是一个算子。算子之间才考虑运算的数据依赖关系。上题的乘法运算可以通过SIMD等方法来解决，但是add的关键路径操作是无论如何都无法解决的。