CNN的使用
本程序可以使用CNN来预测mnist数据集的数字
#CNN from __future__ import division,print_function import tensorflow as tf import matplotlib.pyplot as plt import numpy as np from tensorflow.examples.tutorials.mnist import input_data mnist=input_data.read_data_sets("MNIST_data/",one_hot=True) learning_rate=0.001 training_iters=500 batch_size=128 display_step=10 n_input=784 #数据集中一个照片的像素为28*28=784 n_classes=10 dropout=0.85 x=tf.placeholder(tf.float32,[None,n_input]) y=tf.placeholder(tf.float32,[None,n_classes]) keep_prob=tf.placeholder(tf.float32) def conv2d(x,W,b,strides=1): x=tf.nn.conv2d(x,W,strides=[1,strides,strides,1],padding='SAME') #tf.nn.conv2d方法的四个参数,前两个参数input和filter都在下面介绍了 #strides表示图像在每一维度的步长,第一位和最后一位固定为1,。所以这里仅仅表示行列步长都为1 x=tf.nn.bias_add(x,b)#是这样的,加上偏置值,b是一个行向量,加到x矩阵的每一行中 return tf.nn.relu(x)#激活函数使用ReLU函数 def maxpool2d(x,k=2): return tf.nn.max_pool(x,ksize=[1,k,k,1],strides=[1,k,k,1],padding='SAME') #参考https://blog.csdn.net/m0_37586991/article/details/84575325 #但是这里池化移动的步长为2 #define convnet,其构成是两个卷积层,然后是全连接层,一个 dropout 层,最后是输出层 def conv_net(x,weights,biases,dropout): x=tf.reshape(x,shape=[-1,28,28,1]) #修改batch个像素组成的x,然后作为卷积创建方法tf.nn.conv2d的第一个参数input #参考https://blog.csdn.net/zuolixiangfisher/article/details/80528989 #input参数也有四个参数,第一个是batch,第二第三是图片的高度和宽度, #第四个参数in_channel 为图片的通道数,灰度图该值为1,彩色图为3, #其实通道形象起来就是输入和输出的数目,参照这里的矩阵描述https://blog.csdn.net/m0_37586991/article/details/84575325 #然后batch是可以不用写直接写-1的,因为它会根据 x的实际大小和28,28算出来 conv1=conv2d(x,weights['wc1'],biases['bc1']) #第一个conv层有一个5×5的卷积核,1个输入和32个输出,偏置为32行的 conv1=maxpool2d(conv1,k=2) #最大池化操作,得到了一个池化之后的输出 conv2=conv2d(conv1,weights['wc2'],biases['bc2']) #第二个conv层有一个5×5的卷积核,32个输入和64个输出,偏置为64行的 conv2=maxpool2d(conv2,k=2) fc1=tf.reshape(conv2,[-1,weights['wd1'].get_shape().as_list()[0]]) fc1=tf.add(tf.matmul(fc1,weights['wd1']),biases['bd1']) fc1=tf.nn.relu(fc1) fc1=tf.nn.dropout(fc1,dropout) out=tf.add(tf.matmul(fc1,weights['out']),biases['out']) return out #字典,挑选合适的权值。 weights={ 'wc1':tf.Variable(tf.random_normal([5,5,1,32])), 'wc2':tf.Variable(tf.random_normal([5,5,32,64])), # wc1和wc2 # 根据tf.nn.conv2d方法,这里的w要描述的应该是卷积核 # 四个参数分别是:卷积核高度,卷积核宽度,图像通道数(和input的in_chanel一样),卷积核数量 #实际上就是这层网络的输入和输出,[5,5,1,32]和[5,5,32,64]表示 #第一个conv层有一个5×5的卷积核,1个输入和32个输出。第二个conv层有一个5×5的卷积核,32个输入和64个输出 'wd1':tf.Variable(tf.random_normal([7*7*64,1024])), 'out':tf.Variable(tf.random_normal([1024,n_classes])) } biases={ 'bc1':tf.Variable(tf.random_normal([32])), 'bc2':tf.Variable(tf.random_normal([64])), 'bd1':tf.Variable(tf.random_normal([1024])), 'out':tf.Variable(tf.random_normal([n_classes])) } pred=conv_net(x,weights,biases,keep_prob)#神经网络最后一层的输出 cost=tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred,labels=y)) #具体的操作可以参考https://blog.csdn.net/zj360202/article/details/78582895 #以及https://blog.csdn.net/yhily2008/article/details/80262321 #但是无论如何这就是个供优化器使用的损失函数 optimizer=tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost) #Adam优化器 correct_prediction=tf.equal(tf.argmax(pred,1),tf.argmax(y,1)) accuracy=tf.reduce_mean(tf.cast(correct_prediction,tf.float32)) init=tf.global_variables_initializer() train_loss=[] train_acc=[] test_acc=[] with tf.Session() as sess: sess.run(init) step=1 while step<=training_iters: batch_x,batch_y=mnist.train.next_batch(batch_size)#x是784列的像素描述,y是实际种类,是个10列矩阵 #参照https://blog.csdn.net/weixin_43364556/article/details/102892890即可明白这里的用法 sess.run(optimizer,feed_dict={x:batch_x,y:batch_y,keep_prob:dropout}) if step % display_step==0: loss_train,acc_train=sess.run([cost,accuracy],feed_dict={x:batch_x,y:batch_y, keep_prob:1.}) print('Iter '+str(step) + ', Minibatch Loss= '+\ '{:.2f}'.format(loss_train)+ ', Training Accuracy=' +\ '{:.2f}'.format(acc_train)) acc_test=sess.run(accuracy,feed_dict={x:mnist.test.images,y:mnist.test.labels,keep_prob:1.}) print('Testing Accuracy:'+\ '{:.2f}'.format(acc_train)) train_loss.append(loss_train) train_acc.append(acc_train) test_acc.append(acc_test) step+=1 eval_indices=range(0,training_iters,display_step) plt.plot(eval_indices,train_loss,'k-') plt.title('Softmax Loss per iteration') plt.xlabel('Iteration') plt.ylabel('Softmax Loss') plt.show() plt.plot(eval_indices,train_acc,'k-',label='Train Set Accuracy') plt.plot(eval_indices,test_acc,'r--',label='Test Set Accuracy') plt.title('Train and Test Accuracy') plt.xlabel('Generation') plt.ylabel('Accuracy') plt.legend(loc='lower right') plt.show()
看了这么多我终于明白了。
我一直忽略了一个重要的参数:padding='SAME'和padding='VALID'。
我一直在想,[-1,28,28,1]的输入张量,代表着输入矩阵是一个输入(单通道),28*28的像素,
那么卷积核为[5,5,1,32],表示卷积核的尺寸为5*5,图像通道数(输入通道数),卷积核数目(输
出通道数)。
那么这个卷积核在像素上移动的时候,就会将图片降低到24*24?其实不会这样的,当padding
='SAME'的时候,会自动边界补0(也就是说卷积操作前后图片尺寸不会变化)!!!!!!!!!
然后就是卷积核的数量对应输出张量的通道数。这是显然的,卷积核数目就是输出通道数目。
比如说这里的输入张量是[-1,28,28,1],输出张量就是[-1,28,28,32]。每一个卷积核做一次卷积运算,
最终得到的32个结果合并在一起,组成了下一层神经网络的输入。
然后可能就会有疑问了,那么我为什么要设置32个卷积核呢?我一开始可是只有一张单通道的
28*28像素的初始输入图片啊。怎么一下你说设置32个卷积核,就能得到32通道的输出张量呢?同
一层的32个卷积核都是一样的吗?如果是一样的,那么设置32个卷积核有什么意义?
同一层的32个卷积核当然都不是一样的。你看,我们在定义卷积层1的卷积核1 的时候:
conv1=conv2d(x,weights['wc1'],biases['bc1']),使用到的参数wc1是怎么来的?
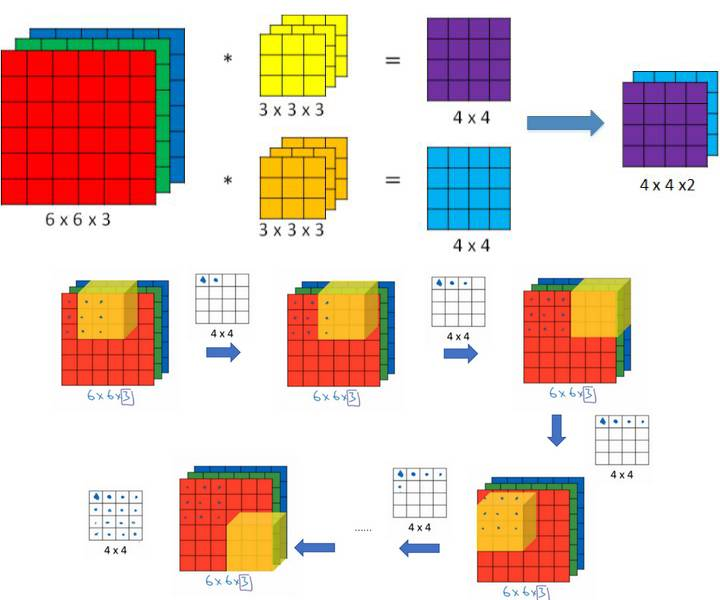
只用看最上面的一行图片就可以了。显然这里的CNN的一层当中,输入是三通道的,有两个卷积核,
输出是双通道的。
然后参数是padding='VALID'。
图片尺寸是6*6,卷积核尺寸是3*3,步长是1。
一个卷积核得到一个4*4的输出。然后两个4*4的输出拼接在一起就形成了双通道的4*4的输出。
然后这里涉及到一个知识点:一个卷积核是怎么样作用于多通道输入数据的呢?
以及卷积层的偏置加在哪里?
还是知乎老哥给力。https://www.zhihu.com/question/288630085/answer/991228760
注意!!!!
对于卷积核的理解,可能很多人都有误区。
那就是,上述图片的单个卷积核,虽然定义的时候说它是3*3的,但是实际的卷积核大小是3*3*3的!
这里的前面的3*3是卷积核的二维尺寸,最后一个3指的是输入通道数!(也就是6*6*3的3通道)。(我发现这些东西害得自己学)
如下图所示,太明显了,懂的看这图就秒懂了。
显然这里是padding='SAME',在外围扩展了一下。
然后输入是三通道的5*5图片,分别是 x1,x2,x3。
有两个卷积核W0和W1,可以看出每个卷积核都有三个对应通道的数据结构。比如W0就有W01,W02,W03。而且它们
的参数都是不相同的!!!
卷积核W0的偏置为b0,卷积核W1的偏置为b1。
输出是每个卷积核对应的两个输出。这两个输出组成了双通道输出。
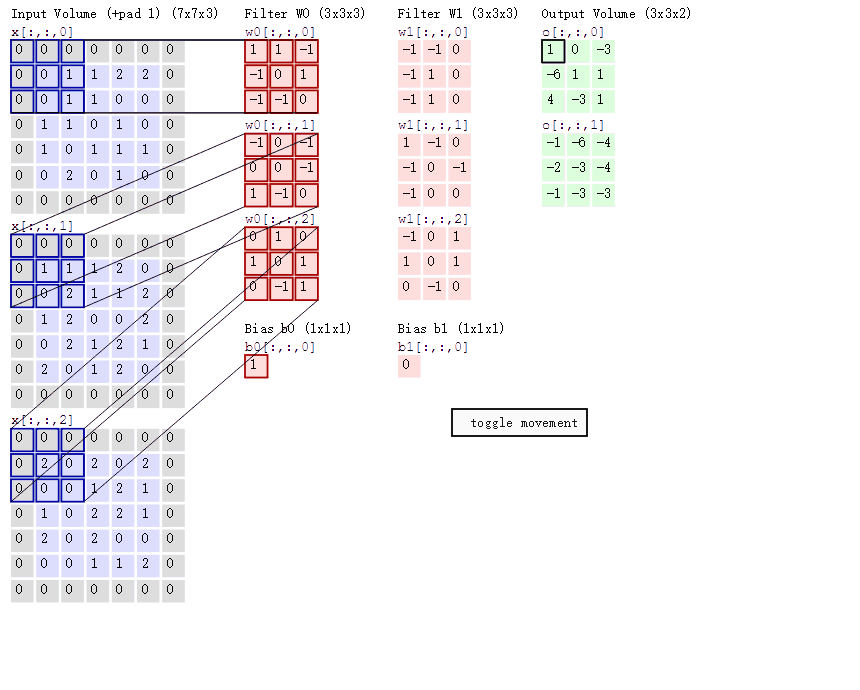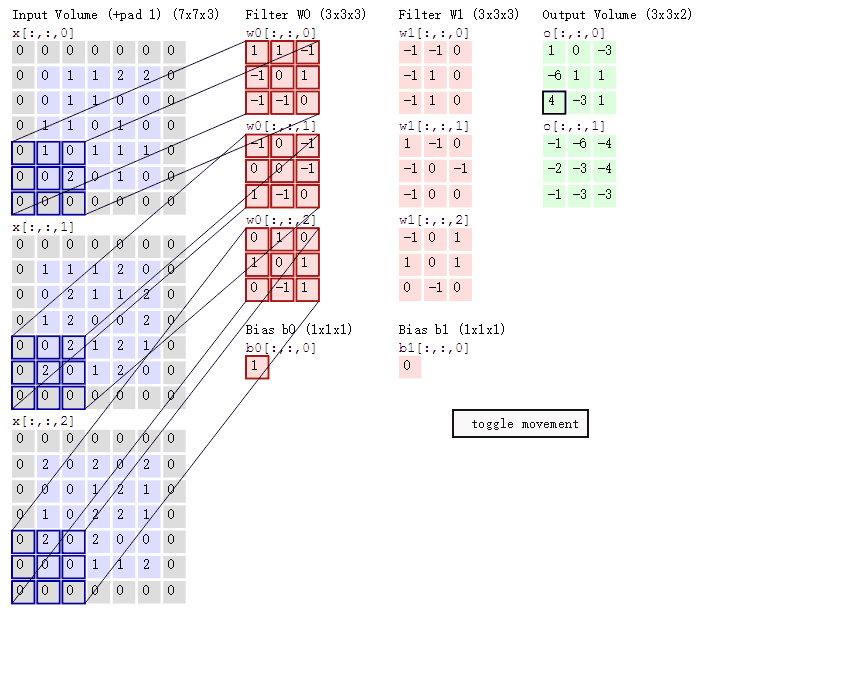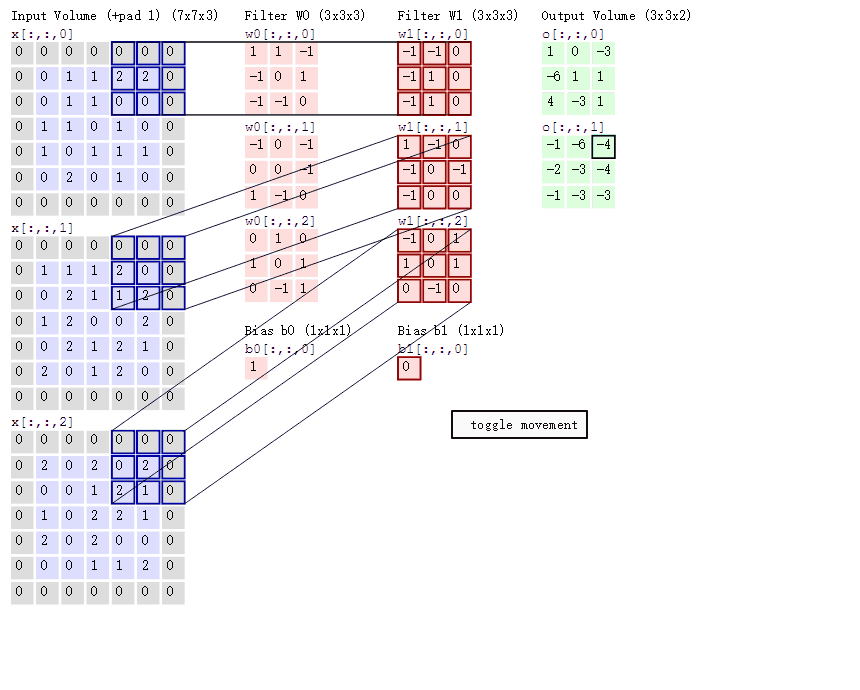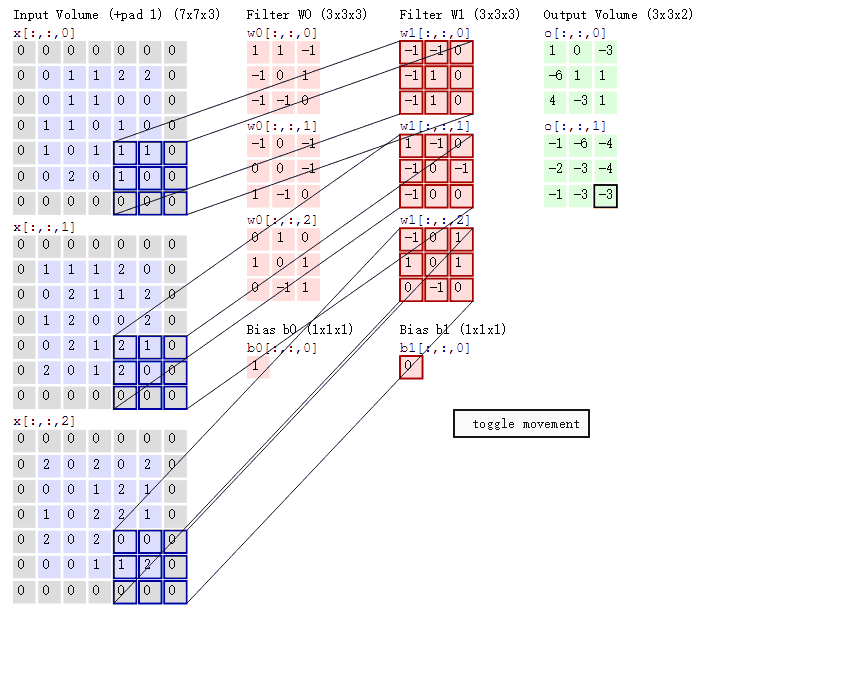
具体的计算方法如图显然可知。
将各个通道与对应的卷积核的对应块做卷积运算。比如X0的最左上角,分别和W01,W02,W03做一次卷积
运算,可以得到三个值,将这三个值和偏置b0相加,就得到了第一个输出通道最左上角的输出。
那么卷积核的构造,卷积核的运算规则,偏置加在哪里就显而易见了。
源代码中的
再举一个例子吧。如下图,就不说明了。
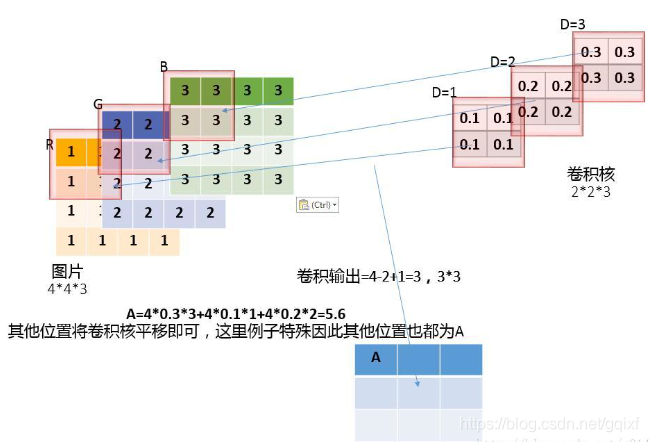
现在我也明白batch的作用是什么了
还是知乎老哥给力。https://www.zhihu.com/question/32673260
这个程序的batch设置为128,和实际的CNN网络的运行没有任何卵关系,我一开始的猜想完全错误。
读懂整个程序之后,我发现CNN还是老一套。单次只能输入一张图片x(最开始的CNN层通道为1),
然后一番处理过后要和y(label)进行比较。
所以之所以设置batch,是因为神经网络的训练需要大量的数据,但是这么多数据不可能一次跑完,
所以设置一个batch分批跑,也许批内还能并行优化处理。
那么全连接层和dropout层的工作原理呢?
我想读一读
conv2=maxpool2d(conv2,k=2) fc1=tf.reshape(conv2,[-1,weights['wd1'].get_shape().as_list()[0]]) fc1=tf.add(tf.matmul(fc1,weights['wd1']),biases['bd1']) fc1=tf.nn.relu(fc1) fc1=tf.nn.dropout(fc1,dropout) out=tf.add(tf.matmul(fc1,weights['out']),biases['out']) return out
这段代码就够了。懂的自然懂。
发现了一个遗漏的问题。我当时没有搞懂。
那就是:为何全连接层的输入为7*7*24?这是怎么确定的?
关键是这段代码我还没有理解透彻。
所以我做了一个测试:
def conv_net(x,weights,biases,dropout): x=tf.reshape(x,shape=[-1,28,28,1]) conv1=conv2d(x,weights['wc1'],biases['bc1']) #第一个conv层有一个5×5的卷积核,1个输入和32个输出,偏置为32行的 ret1=conv1 conv1=maxpool2d(conv1,k=2) #最大池化操作,得到了一个池化之后的输出 ret2=conv1 conv2=conv2d(conv1,weights['wc2'],biases['bc2']) #第二个conv层有一个5×5的卷积核,32个输入和64个输出,偏置为64行的 ret3=conv2 conv2=maxpool2d(conv2,k=2) ret4=conv2 fc1=tf.reshape(conv2,[-1,weights['wd1'].get_shape().as_list()[0]]) ret5=fc1 fc1=tf.add(tf.matmul(fc1,weights['wd1']),biases['bd1']) ret6=fc1 fc1=tf.nn.relu(fc1) fc1=tf.nn.dropout(fc1,dropout) ret7=fc1 out=tf.add(tf.matmul(fc1,weights['out']),biases['out']) return ret1,ret2,ret3,ret4,ret5,ret6,ret7,out
在session运行时获取这些tensor,这些Tensor读取之后变成numpy array,然后用.shape方法读取他们的形状。
最终结果为:
ret1:(128, 28, 28, 32) ret2:(128, 14, 14, 32) ret3:(128, 14, 14, 64) ret4:(128, 7, 7, 64) ret5:(128, 3136) ret6:(128, 1024) ret7:(128, 1024) out:(128, 10)
不难看出,答案直接一目了然了。
首先,池化操作中的padding=‘SAME’和卷积计算过程中的padding=‘SAME’不太一样。前者是会改变结果的形状的。这里最大化池的k=2,因此结果张量的行列都缩小了一半。
然后我们看(128,28,28,32)显然依次是batch数,矩阵行列(像素),通道数(卷积核数目)。
fc1=tf.reshape(conv2,[-1,weights['wd1'].get_shape().as_list()[0]])
上面的这句代码,将conv2从(128,7,7,64)的形状改变为了(128,7*7*64),怎么做到的呢?reshape的功能不用多说,后面的代码获取了张量weights['wd1']的形状的第一维度,7*7*64来作为conv2的第二维度,第一维度缺省为128,刚好为batch数目。这个过程就是把张量压缩到一维来和全连接层对接。
然后全连接层的实质也因此看的很清楚了,就是矩阵相乘。所有数据单拉出来相乘。
fc1=tf.add(tf.matmul(fc1,weights['wd1']),biases['bd1'])
就是这么简单,全连接层。
weights['wd1']就是【7*7*64,1024】维度的随机矩阵,刚好能和【batch,7*7*64】的输入数据相乘。根据线性分类器的经验,【batch,7*7*64】的这个全连接层的输入数据,的行,的行中的列数,刚好就是全连接层的输入数据。
所以全连接层的输入数据数目不是前面的卷积层的64个输出!!!而是卷积层摊平之后的7*7*64!!!
然后卷积层的运算也很简单,想一想矩阵乘法的规则,就是一个batch中的7*7*64个输入点,和【7*7*64,1024】这个随机矩阵的1024个列的每一列的7*7*64个元素做乘积累加,最终就得到了(batch,1024),这就是全连接。就是线性代数的玩意。
然后第二次全连接得到了(batch,10)这个最终的CNN网络输出pred。
而这也和
最终疑问:为什么一层当中需要设置多个卷积核?多个卷积核有什么作用?
https://blog.csdn.net/zuolixiangfisher/article/details/80528989




