简单线性回归&&损失函数&&优化器&&boston数据集读取&&数据显示
这里介绍了一个最简单的使用TensorFlow实现简单的线性回归算法的方法。
http://c.biancheng.net/view/1906.html原文地址
import tensorflow as tf import numpy as np import matplotlib.pyplot as plt def normalize(X): """Normalizes the arry X""" mean=np.mean(X) std=np.std(X) X=(X-mean)/std return X #Boston boston=tf.contrib.learn.datasets.load_dataset('boston') X_train,Y_train=boston.data[:, 5],boston.target#list二维切片 #X_train=normalize(X_train)### n_samples=len(X_train) X=tf.placeholder(tf.float32,name='X') Y=tf.placeholder(tf.float32,name='Y') b=tf.Variable(0.0) w=tf.Variable(0.0) Y_hat=X*w+b #loss function loss=tf.square(Y_hat-Y,name='loss') #Gradient descent optimizer=tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(loss) init_op=tf.global_variables_initializer() total=[] with tf.Session() as sess: sess.run(init_op) writer=tf.summary.FileWriter('graphs',sess.graph) for i in range(100): total_loss=0 for x,y in zip(X_train,Y_train): _,l=sess.run([optimizer,loss],feed_dict={X:x,Y:y}) ###？？？ total_loss+=l total.append(total_loss/n_samples) print('Epoch {0}: Loss {1}'.format(i,total_loss/n_samples)) writer.close() b_value,w_value=sess.run([b,w]) Y_pred=X_train*w_value+b_value print('Done') plt.plot(X_train,Y_train,'bo',label='Real Data') plt.plot(X_train,Y_pred,'r',label='Predicted Data') plt.legend() plt.show() plt.plot(total) plt.show()
从上到下依次解析一下代码
1.标准化函数
def normalize(X):
目前还不知道这东西的作用。
2.读取波士顿房价数据集
然后
3.boston.data[:,5]的切片操作
补充一个二维切片操作
L=np.array([[1,2,3,4,5],[1,2,3,4,5]]) A,B=L[:,4],1 print(A) print(B)
当[:,4],A输出[5,5]，4改为0，A输出[1,1],
而且L必须是np array。
那么就不难理解这个操作的作用了。
http://lib.stat.cmu.edu/datasets/boston这个是波士顿房价
本文的线性回归的目的是 最后一项MEDV（房价）和第六项RM（房间数量）之间的线性回归关系。
这个切片就是，boston读取进来之后是列向量矩阵，然后
boston.data[:,5]可以读取每个列向量的第六项，重新按顺序组合成一个新的list。
简单读一读代码就明白了。
4 损失函数
线性回归问题的损失函数就是方差。
训练的本质目的就是使得损失函数最小化。（损失函数为0时可能过拟合）
本程序中的损失函数为：loss=tf.square(Y_hat-Y,name='loss')
即loss=tf.square(X*w+b - Y)
5 TensorFlow优化器
优化器可以降低损失函数，并得到训练后的参数。
在这个程序里，需要得到的参数就是b和w。最终的回归方程就是y=x*w+b。
优化器有许多种，这里使用其中一种，tf.train.GradientDescentOptimizer。
优化器的使用很简单，只有一个参数learning_rate
可以看到下面的参数的更新方法。参数在梯度的负方向上被下降了，并且下降量还要乘以
一个learning_rate。
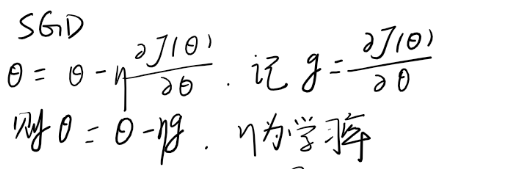
https://www.cnblogs.com/cccczh/p/11874482.html
6 TensorBoard可视化
直接在会话中
writer=tf.summary.FileWriter('graphs',sess.graph)
一句话搞定
7 TensorFlow的训练过程
上面的都懂了这里也不用多说了。
直接看上面的大循环代码。
8 训练结果可视化
