leetcode11 一点新感悟

 

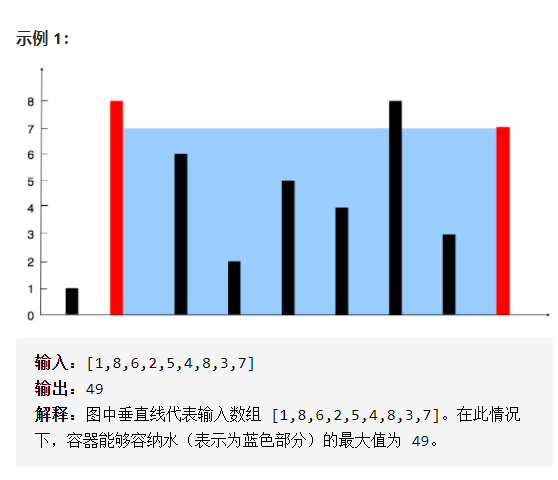
 　　这题图是这样的。

　　

最优矩形问题
求max{(j-i)*min(a[i],a[j])},(j>i)

首先我们确定了i，那么问题就变成了在它的右边找到这样的一个j
使得矩形面积最大，这就是对于i的最优解。

想要试验出这个j的pos势必要遍历i右边的全部点？
是的，因为可能最右边的点的高度等于i点的高度，这就是最优解。

 

。。。没想到这题思路居然是这样的
思路就是两个指针，一个在首部，一个在尾部，每次移动
两个指针当中的较低端，向中间移动（因为较低的移动才有可能使得总面积变大）

　　我悟了，就是移动两者较低的，才一定会获得最优解。

　　怎么样呢？就是一个状态，暴力解法中，所有的情况留在了n^2种情况当中。

　　左右两个指针，移动一个的时候，势必会丢失掉一些状态，比如上图，假设两个指针一个最左边i=0一个最右边j=8。

如果i移动到了i=1，那么就会丢失(i=0,j=7),(i=0,j=6)...直到(i=0,j=1)这些情况。但是没有关系的，左右两个指针高度取的

是最小值，上述这些情况两侧高度最小值最大都不可能超过a[0]了，而且底部宽度还在变小，所以这样的算法是不会遗漏

掉最优解的。

　　

代码如下：

#include<bits/stdc++.h>
using namespace std;
class Solution {
public:
    int maxArea(vector<int>& height)
    {
        int l=0;
        int r=height.size()-1;
        int res=0;
        while(l<r)
        {
            res=max(res,(r-l)*min(height[l],height[r]));
            if(height[l]<height[r])
            {
                l++;
            }
            else
            {
                r--;
            }
        }
        return res;
    }
};
int main()
{
    Solution s;
    vector<int>a={1,8,6,2,5,4,8,3,7};
    cout<<s.maxArea(a)<<endl;
    return 0;
}