Java集合源码分析：平衡二叉树（AVL Tree）
在上一章的文章中，我们讲到了二叉排序树，它很好的平衡了插入与查找的效率，但二叉排序树如果不平衡，那么查找效率就会大大降低，今天要讲的这个平衡二叉树就是一种解决这个问题的方法。
一、平衡二叉树的定义
平衡二叉树 是一种二叉排序树，其中每一个节点的左子树和右子树的高度差至多等于1 。它是一种高度平衡的二叉排序树。意思是说，要么它是一棵空树，要么它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1 。我们将二叉树上结点的左子树深度减去右子树深度的值称为平衡因子BF (Balance Factor)，那么平衡二叉树上所有结点的平衡因子只可能是-1 、0 和1。
这里举个栗子：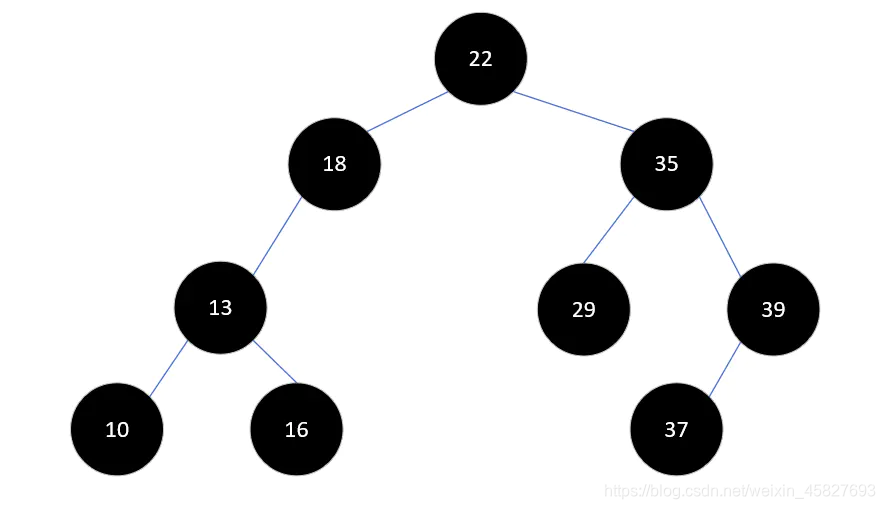
仔细看图中值为18的节点，18的节点的深度为2 。而它的右子树的深度为0，其差值的绝对值大于1了，所以这不是一科平衡二叉树。
二、平衡二叉树的实现原理
平衡二叉树构建的基本思想就是在构建二叉排序树的过程中，每当插入一个节点时，先检查是否因插入而破坏了树的平衡性，如果是，则找出最小不平衡二叉树。在保持二叉排序树特性的前提下，调整最小不平衡子树中各节点之间的链接关系，进行相应的旋转，使之成为新的平衡子树。最小不平衡子树是指距离插入节点最近，且平衡因子的绝对值大于1的节点为根的子树。
下面就让我们通过一个栗子来看看平衡二叉树是怎么构建的呢
首先我们将{3, 2, 1, 4, 5, 6, 7, 10, 9, 8}这样的数组构建成一个二叉排序树，按照二叉排序树的性质，我们将得到下图这样的树：
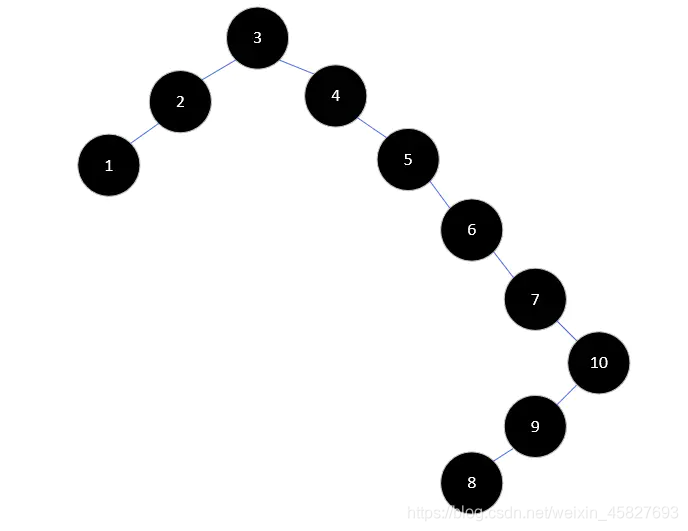
从图中可以看出，树的高度达到了8，对于查找和插入效率肯定是不够理想的。
接下里我们来看看怎么将这颗二叉排序树一步步构建成平衡二叉树的：
1.按数组顺序将2和3插入，此时没有什么影响，3的平衡因子为1， 2的平衡因子为0，到这里还没什么问题
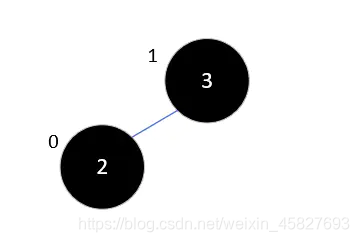
2.此时我们再来插入1，根据二叉排序树，1只能是2的左子树，然而此时3的平衡因子为2，已经不符合平衡二叉树的规则，这个时候，这棵树就是最小不平衡子树
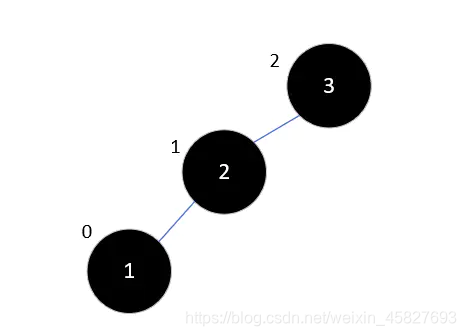
3.我们将其右旋：三个元素的平衡因子都为0，没什么毛病，我们继续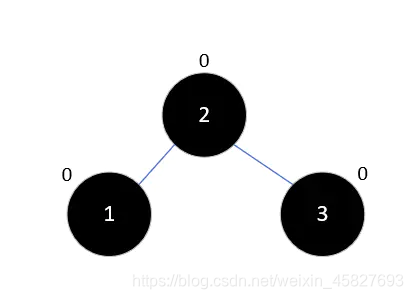
4.在插入4，根据二叉排序树的规则，4只能放在3的右子树，此时没什么大毛病，我们继续
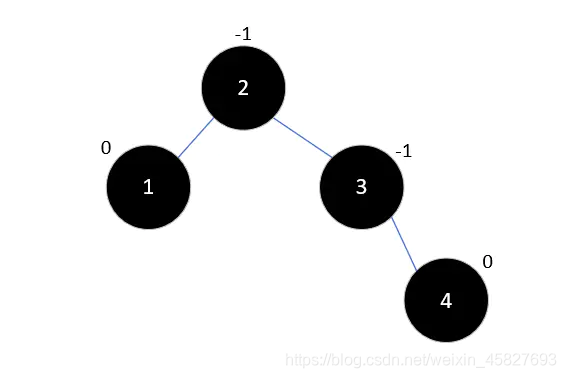
5.在插入元素5，同理，5只能放在4的右子树，此时元素2的平衡因子为2大于1，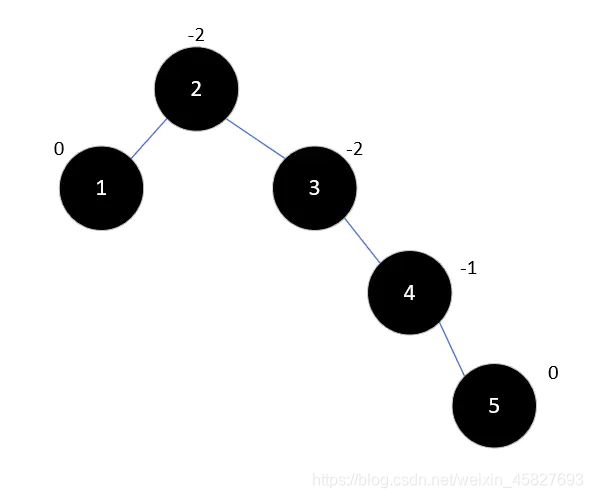
6.将其左旋：没什么大毛病，我们继续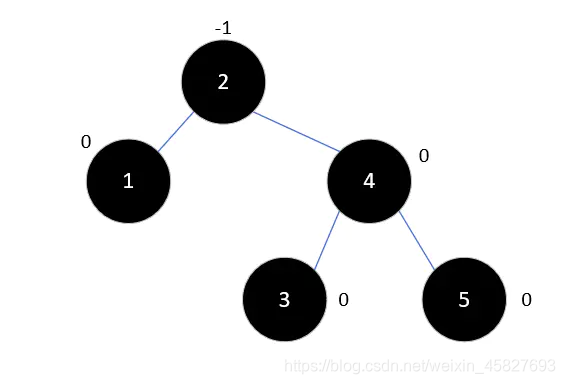
7.在插入元素6，此时为最小不平衡子树
8.再将其左旋，这里具体怎么左旋，就这么想，就是在满足二叉排序树性质的同时，让根节点左边的深度增加，右子树的深度减小，以达到满足二叉平衡树的性质。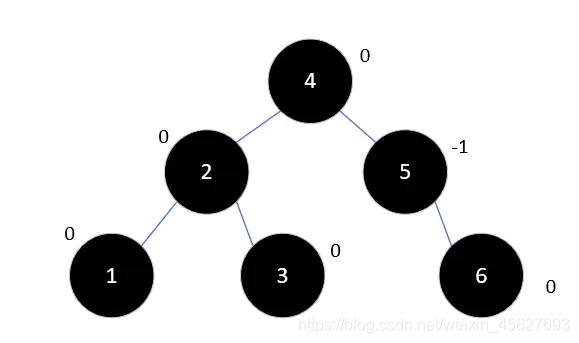
接下来的过程大家可以自行去尝试做出来
这里我把最后的结果贴出来，如果有疑问，可在评论区留言讨论！
最终结果：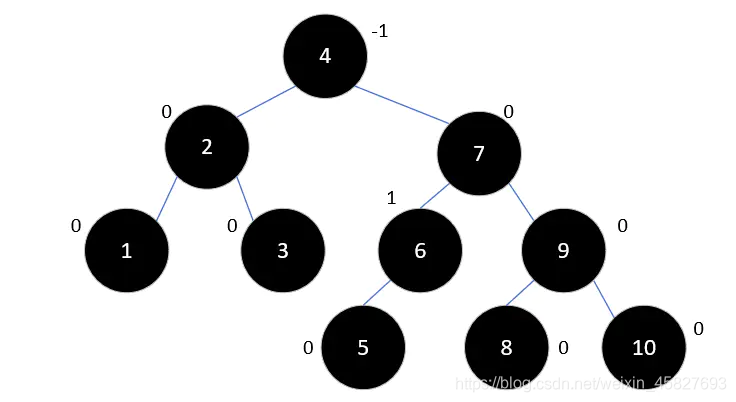
可以看到，最后树的高度仅为4，比之前的8对比来说，效率就高了近一半。
平衡二叉树的删除操作与插入类似，这里将不再介绍。大家可以自己思考如何最高效地删除元素，可以分叶结点、仅有一个子结点和有两个子结点三种情况考虑，这里还用到了递归的思想。
这一次的讨论就到这里，欢迎小伙伴们留言讨论！
