算法基本概念

算法（Algorithm）：一个计算过程，解决问题的方法

Niklaus Wirth: “程序=数据结构+算法”

时间复杂度

时间复杂度：用来评估算法运行效率的一个参考依据

# 			算法										时间复杂度

#		print('Hello World')							O(1)

#        for i in range(n): 							O(n)
#           print('Hello World')

#        for i in range(n): 							O(n^2)
#            for j in range(n): 
#                print('Hello World')

#        for i in range(n): 							O(n^3)
#            for j in range(n): 
#                for k in range(n): 
#                    print('Hello World')

# 		此时虽然是打印三次，但是对于计算机来说有限次的打印都不是事，所以复杂度还是O(1)
#		 print('Hello World') 
#        print('Hello Python') 
#        print(‘Hello Algorithm’)					    O(1)

#		每次循环都会减少问题规模的一半，当算法中出现折半算法时，时间复杂度都会出现O(logn)
#       O(logn)是O(log2n)的简写
#        while n > 1:   								O(logn) 
#            print(n)    
#            n = n // 2

---

时间复杂度小结

- 时间复杂度是用来估计算法运行时间的一个式子（单位）。 
- 一般来说，时间复杂度高的算法比复杂度低的算法慢。 
- 常见的时间复杂度（按效率排序） 
	O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n2logn) < O(n3) 
- 复杂问题的时间复杂度 
	O(n!) O(2n) O(nn) …

---

简单快速判断算法的时间复杂度

# 快速判断算法复杂度（适⽤用于绝⼤大多数简单情况）： 
- 确定问题规模n 
- 循环减半过程→logn 
- k层关于n的循环→nk 
复杂情况：根据算法执⾏行行过程判断

空间复杂度

# 空间复杂度：用来评估算法内存占用大小的式子 
- 空间复杂度的表示方式与时间复杂度完全一样 
- 算法使用了有限变量：O(1) 
- 算法使用了长度为n的一维列表：O(n) 
- 算法使用了m行n列的二维列表：O(mn) 

# “空间换时间”

递归

递归的两个特点：

• 调用自身
• 结束条件

def func1(x):    
    print(x) 
    func1(x-1)
    
def func2(x):    
    if x>0:        
        print(x) 
        func2(x+1)
        
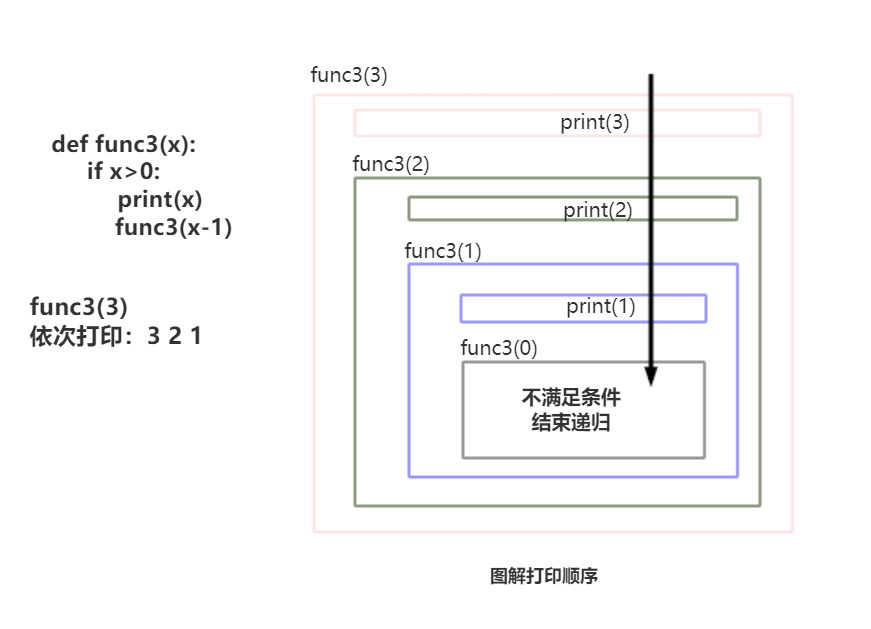
def func3(x):    
    if x>0:        
        print(x) 
        func3(x-1)
        
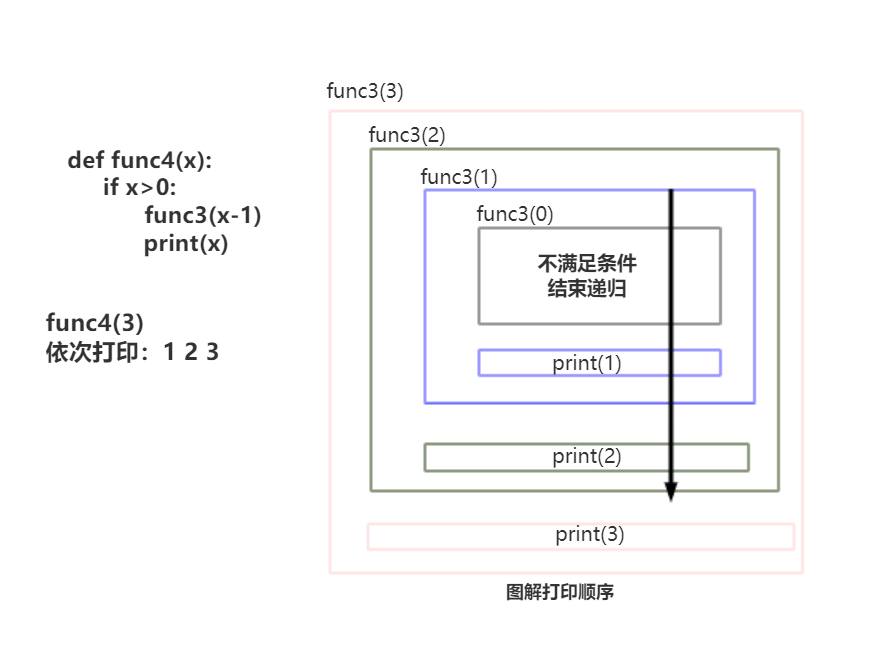
def func4(x):    
    if x>0: 
        func4(x-1)        
        print(x)
        
# func1不是递归，fuc2不是递归
# func3 和 func4是递归，打印的先后顺序不同

func3(3) 的打印结果：先打印后递归

程序的执行顺序从上往下

func4(3) 的打印结果：先递归后打印