PCA数学推导及原理（转）

原文：https://zhuanlan.zhihu.com/p/26951643

在多元统计分析中，主成分分析（Principal components analysis，PCA）是一种分析、简化数据集的技术。主成分分析经常用于减少数据集的维数，同时保持数据集中的对方差贡献最大的特征。这是通过保留低阶主成分，忽略高阶主成分做到的。这样低阶成分往往能够保留住数据的最重要方面。

PCA在机器学习中经常被用到，是数据预处理的重要步骤。它主要基于以下考虑：

• 高维特征中很多特征之间存在相关性，含有冗余信息
• 相比于低维数据，高维数据计算更复杂

PCA的数学原理

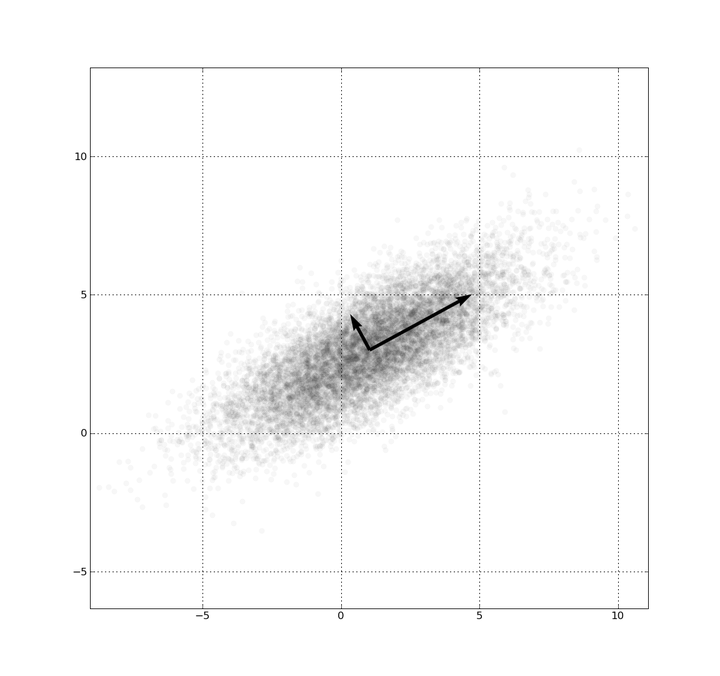
如下图，平面上有很多二维空间的特征点，如果想对这些特征点做特征降维（变为一维），应该怎么做呢？大家应该都知道需要进行投影，但还要考虑在哪个方向上进行投影，例如图中需要投影到长箭头方向即可，但考虑为什么不在短箭头上投影？

PCA本质上是一个有损的特征压缩过程，但是我们期望损失的精度尽可能地少，也就是希望压缩的过程中保留最多的原始信息。要达到这种目的，我们希望降维（投影）后的数据点尽可能地分散。如图，相比于长箭头，如果在短箭头上进行投影，那么重叠的点会更多，也就意味着信息丢失的更多，因而选择长箭头方向。

 

基于这种思想，我们希望投影后的数据点尽可能地分散。而这种分散程度在数学上可以利用方差来表示。设降维后的特征为，也就是希望尽可能地大（为特征中的值，为均值），而由于在PCA降维前，一般已经做了特征零均值化处理，为了方便，记。

同样，为了减少特征的冗余信息，我们希望降维后的各特征之间互不相关。而不相关性可以用协方差来衡量。设降维后的两个特征为、，则希望为0。

现假设我们的数据为

构造出协方差矩阵，并乘以系数，则

可以看出的对角线元素就是各特征的方差，其他各位置的元素就是各特征之间的协方差。因而只需要降维后的数据协方差矩阵满足对角矩阵的条件即可。

设为原始数据做完PCA降维后的数据，满足（矩阵乘法相当于映射，若为的列向量为基向量，那么就相当于映射到新的坐标系），，分别为对应的协方差矩阵，那么

因而，我们只需要计算出，使满足对角矩阵的条件即可。而为实对称矩阵，我们只需要对它做矩阵对角化即可。

PCA的原理基本就是这样，还是挺简单的。

 

PCA的推导证明

PCA的构建：PCA需要构建一个编码器，由输入得到一个最优编码（若，则做了降维编码）；同时有一个解码器，解码后的输出尽可能地与相近。

PCA由我们所选择的解码器决定，在数学上，我们使用矩阵将映射回，即，其中定义解码的矩阵。

为了限制PCA的唯一性，我们限制中所有列向量彼此正交且均有单位范数（否则、同比例增加、减少会产生无数个解）。

在数学上，为了满足PCA构建中的条件，我们利用范数来衡量与的相近程度。即，也就是

该最小化函数可以简化为

因而，优化目标变为，再带入，

再求偏导

于是我们可以得到编码函数，PCA的重构操作也就可以定义为。问题接着就转化成如何求编码矩阵。由于PCA算法是在整个数据矩阵上进行编码，因而也要用对所有数据进行解码，所以需要最小化所有维上的误差矩阵的Frobenius范数：

我们考虑的情况，则是一个单一向量，则上式可以转化为

而为标量，转置与自身相等，上式通常写作

再将每一个输入点叠加起来，我们得到

Frobenius范数简化成（考虑约束条件）

最后的优化目标可以利用以及拉格朗日乘数法来求解，可得最优的是的最大特征值对应的特征向量。

上面的推导特定于的情况，仅有一个主成分。一般来说，矩阵由的前个最大的特征值对应的特征向量组成（利用归纳法，将表示为的函数即可，需要两个辅助矩阵：单位对角矩阵以及，省去证明过程）。

参考

• 主成分分析
• CodingLabs - PCA的数学原理
• 《Deep Learning》 Ian Goodfellow et al.