集成学习-学习笔记
集成学习:
通过构建多个学习器完成学习任务。主要分为两类:
1. 多个学习器之间存在强依赖关系,必须串行生成序列化方法。代表为Boosting提升方法。
2. 多个学习器之间不存在强依赖关系,可同时生成并行化方法。代表为Bagging和随机森林。
文章结构:
1. 前向分步算法介绍
2. 前向分步算法推导出AdaBoost及提升树算法
3. Bagging及随机森林简介
4. 集成学习性能度量
前向分步算法:
在给定训练数据及损函数情况下,前向分步算法能从前往后,每一步通过优化损失函数,只学习一个基函数及其系数,逐步逼近优化函数目标。
其中损失函数分为指数函数,平法损失函数及一般式。

AdaBoost 提升算法具体过程:
先介绍提升算法,之后证明如何用前向分步算法推倒提升算法。
AdaBoost: 通过改变训练样本的权重,学习多个分类器,并将这些分类器进行线性组合,提高分类性能。
问题:
1. 如何改变训练权重及概率分布?
提高前一轮弱分类器分类错误样本权值,降低被正确分类样本权值。如此,加大误分类数据关注度。
2.如何将弱分类器组合成强分类器?
加权多数表决,加大误差率小的弱分类器取值,使其在表决中起较大作用。
算法实现过程:


说明:
1. 第一步。初始化权值分布,假设权值均匀分布。
2. 反复学习,m为迭代次数。
(a) 由初始化的权值分布得到初始分类器。
(b) 计算误差率。
(c) 为基本分类器Gm(x)的重要程度,其随着em的减小而增大,所以误差率越小。其所占权重越大(用于最终加权表决中)
(d) Wm+1,i权重分布。正确分类/误分类=e-2α,及前面说的提高误分类样本权重。
3.最后得到最终分类器,其为基本分类器的线性组合,系数表示其重要程度。
AdaBoost关键部分代码实现(参考机器学习实战)
1 def stumpclassify(datamatrix,dimen,threshval,threshinq): # 对数据进行分类,采用输出扰动方法,提升基学习器之间的多样性 2 retarray=ones((shape(datamatrix)[0],1)) 3 if threshinq=='lt': 4 retarray[datamatrix[:,dimen]<=threshval]=-1 5 else: 6 retarray[datamatrix[:,dimen]>threshval]=-1 7 return retarray 8 def buildstump(dataarr,classlabels,D): ##构建回归树桩 D为每一轮权值 9 datamatrix=mat(dataarr) 10 classlabelvec=mat(classlabels) 11 m,n=shape(datamatrix) 12 beststump={} 13 stumpclass=mat(zeros((m,1))) 14 stepnum=10.0 15 minerror = inf 16 for i in range(n): 17 datamax=datamatrix[:,i].max() 18 datamin=datamatrix[:,i].min() 19 steprange=datamax-datamin 20 stepsize=steprange/stepnum 21 for j in range(-1,int(stepnum)+1): ##进行分类,具体方式参加决策树一章。自我理解通过输入参数扰动等方法增加基分类器的多样性,提高最终分类器性能 22 for ineq in ['lt','gt']: 23 threshval=datamin+stepsize*j 24 retarray=stumpclassify(datamatrix,i,threshval,ineq) 25 error=mat(ones((m,1))) 26 error[retarray==classlabelvec]=0 27 weighterror=D.T*error 28 if weighterror<minerror: 29 minerror=weighterror 30 beststump['ineq']=ineq 31 beststump['threshval']=threshval 32 beststump['dim']=i 33 stumpclass=retarray 34 return beststump,minerror,stumpclass 35 def adaboosttrainsds(dataarr,classlabels,numit=40): ##更新系数过程 36 weakclassast=[] 37 m=shape(dataarr)[0] 38 D=mat(ones((m,1))/m) 39 aggclassest=mat(zeros((m,1))) 40 for i in range(numit): 41 beststump,error,stumpclass=buildstump(dataarr,classlabels,D) ##得到基分类器 42 alpha=float((0.5*log((1.0-error)/max(error,1e-16)))) ##计算α值 43 beststump['alpha']=alpha 44 weakclassast.append(beststump) 45 expon=multiply(-1*alpha*mat(classlabels).T,stumpclass) 46 D=multiply(D,exp(expon)) 47 D=D/D.sum() ##得到更新后的权值 w 48 aggclassest+=alpha*stumpclass 49 aggerror=multiply(sign(aggclassest)!=mat(classlabels).T,ones((m,1))) ##计算累计错误 50 errorat=aggerror=aggerror.sum()/m 51 if errorat==0.0: ##错误率为0时停止循环 52 break 53 return weakclassast
前向加法模型解释Adaboost算法
可由前向分步算法推论出AdaBoost方法。此为损失函数为指数函数形式,推论每一版本的权值更新系数及新分布的形式。新分布的权值更新系数 w 可理解为原分步系数及损失函数乘积,可从残差逼近思想理解。
证明过程(参考统计学习方法证明,其实机器学习书中证明更加简洁明了):


误差分析:
可推论出AdaBoost误差随着每一轮更新,呈指数形式下降,所以性能很好。(证明见书)
提升树:
由前向分步算法推论得出的,通过计算残差,可得每一轮更新的基函数,最后得出最终分类器。此时损失函数为平方损失函数,由此可推论出最终模型。
证明:

提升树算法实现过程:

经过一轮轮迭代,可得最后的分类器。
梯度提升:
对一般的损失函数(非平方及指数损失函数时),可以梯度提升方法。将残差r改为损失函数对基函数的导数即可。

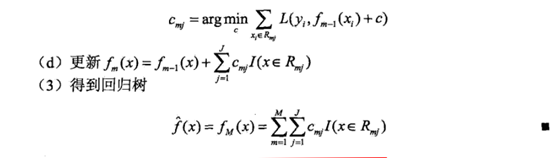
Bagging和随机树森林
Bagging:自助采样,生成T个训练集,之后在每个训练集上生成一个基学习器,之后生成最终的学习器。优点是自助采样,每个训练集仍有部分未使用数据,可用于保外估计,分析其泛化性能。
随机森林:Bagging的升级版,加入了随机属性选择。可随机选择K个属性进行划分。增加基学习器的差异性。
基学习器的结合策略:
- 平均法及加权平均法。
- 投票法及加权投票法。
- 学习法,即通过另一个学习器进行结合。从第一次得出的结果之上,重新生成一个学习器,对该结果进行学习,最终得出分类结果。
多样性及多样性度量:
个体学习器多样性越好,准确性越高,则集成越好。(证明略)
如何提高多样性:
对数据样本,输入属性,输出表示,算法参数进行扰动。



