空间滤波
空间滤波是基础中的基础。其实就是按块像素做运算,比如平滑,锐化等等。分为卷积和相关,其实卷积就是相关的滤波核旋转180。
下图是相关及卷积
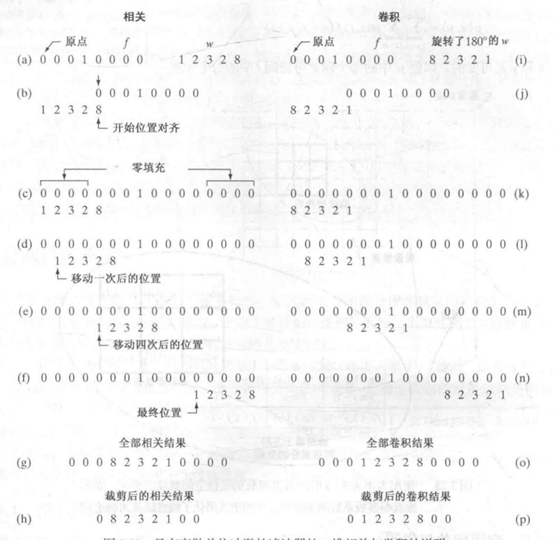
二维类似,对图像进行处理一般使用二维结构。

卷积公式:
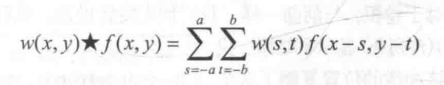
接下来做一下平滑和锐化滤波的代码复现
1、 平滑滤波
一般3*3卷积核,求某邻域内均值,也可能对不同邻域的像素值赋予不同的权重。总之就是利用邻域的均值来消除噪声。还有排序滤波,其实就是取中值。卷积核的大小一般优图像细节信息来决定。若卷积核大于最小的细节信息,就会把该细节信息模糊掉。平滑滤波操作和深度学习中的pooling很相似。以3*3的卷积核为例,做均值滤波,卷积核选取以下卷积核
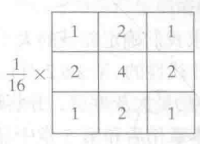


代码
1 void smooth(Mat src) 2 { 3 int IMGH = src.rows; 4 int IMGW = src.cols; 5 unsigned char* d = src.data; 6 int step = src.step; 7 Mat dst(src.size(), CV_8UC1); 8 unsigned char* s = dst.data; 9 for (int i = 1; i < IMGH-1; i++) 10 { 11 for (int j = 1; j < IMGW-1; j++) 12 { 13 s[i*step + j] =(d[(i - 1)*step + j - 1] + d[(i - 1)*step + j] * 2 + d[(i - 1)*step + j + 1] + d[i*step + j - 1] * 2 + d[i*step + j] * 4 + d[i*step + j + 1] * 2 + d[(i + 1)*step + j - 1] + d[(i + 1)*step + j] * 2 + d[(i + 1)*step + j + 1])/16; 14 } 15 } 16 imshow("平滑后结果", dst); 17 imshow("原图", src); 18 imwrite("平滑后结果.jpg", dst); 19 imwrite("原图.jpg", src); 20 waitKey(0); 21 }
2、 锐化
锐化就是求梯度,突出边缘信息,也即求梯度。
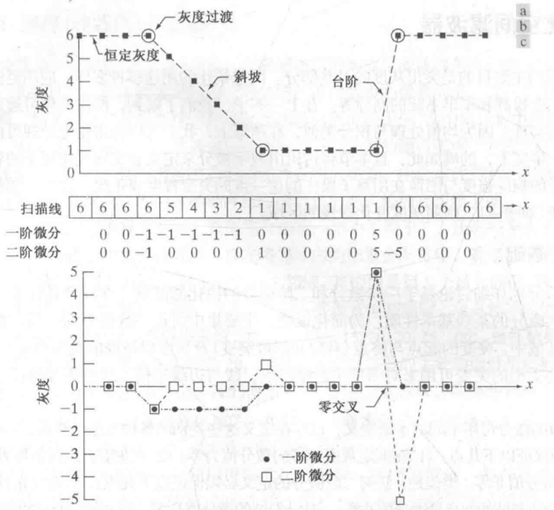
注意一阶微分和二阶微分的差别,在突变处,二阶变化更明显,能分辨是增加还是减少,且存在两个突变,双边缘,更能显示细节信息,但是抗噪性不好。
一阶微分分为 罗伯特交叉算子,sobel算子,我一般都使用sobel算子计算。
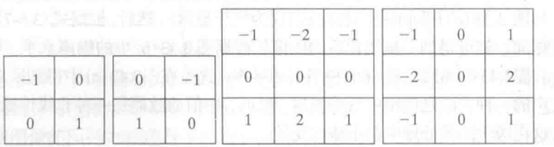
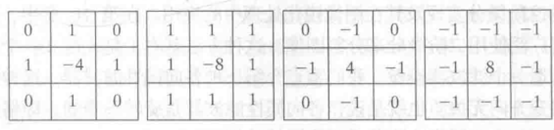
前两幅为xy方向的罗伯特交叉算子,后两幅为sobel算子。
1 void sobel2(Mat src) 2 { 3 int IMGH = src.rows; 4 int IMGW = src.cols; 5 unsigned char* d = src.data; 6 int step = src.step; 7 8 Mat px(src.size(), CV_16SC1,Scalar(0)); 9 Mat py(src.size(), CV_16SC1, Scalar(0)); 10 Mat pxy(src.size(), CV_16SC1, Scalar(0)); 11 int stepxy = px.step; 12 unsigned char* x = px.data; 13 unsigned char* y = py.data; 14 for (int i = 1; i < IMGH - 1; i++) 15 { 16 for (int j = 1; j < IMGW - 1; j++) 17 { 18 x[i*stepxy + j*(stepxy/step)] =abs( d[(i - 1)*step + j - 1]*(-1) + d[(i - 1)*step + j] * (-2) + d[(i - 1)*step + j + 1] *(-1) + d[(i + 1)*step + j - 1] + d[(i + 1)*step + j] * 2 + d[(i + 1)*step + j + 1]); 19 y[i*stepxy + j*(stepxy / step)] = abs(d[(i - 1)*step + j - 1] * (-1) + d[(i - 1)*step + j + 1] + d[i*step + j - 1] * (-2) + d[i*step + j + 1] * 2 + d[(i + 1)*step + j - 1] * (-1) + d[(i + 1)*step + j + 1]); 20 } 21 } 22 addWeighted(px, 0.5, py, 0.5, 0,pxy); 23 Mat px8(src.size(), CV_8UC1, Scalar(0)); 24 Mat py8(src.size(), CV_8UC1, Scalar(0)); 25 Mat pxy8(src.size(), CV_8UC1, Scalar(0)); 26 27 convertScaleAbs(px, px8); 28 convertScaleAbs(py, py8); 29 convertScaleAbs(pxy, pxy8); 30 31 imwrite("方向x.jpg", px8); 32 imwrite("方向y.jpg", py8); 33 imwrite("方向xy.jpg", pxy8); 34 waitKey(0); 35 36 }
图像



二阶微分为 拉普拉斯算子
下图为两种不同类型的拉普拉斯算子。不复现了