【渲染学习随笔】几何坐标变换

（首先，几何坐标变换是计算机图形学一个很重要的题目，由于我之前在学图形学的时候没有很理解这一块，所以打算好好补一补这块内容。本文梳理一些渲染器流水线上概念性的东西，不会涉及太多的数学推导。如有不对，还请指正。）

---

在现在的电影和游戏中，我们可以在屏幕上看到很多立体的物体。然而我们看到的 3D 物体却并非是渲染器直接渲染得来的。

因为渲染器无法直接渲染 3D 物体（因为我们最终看到的是一个*面，即屏幕上的图像信息），我们所看到的 3D 图形都是经由一系列的坐标变换由 3D 物体投影到 2D 屏幕。其中涉及到了 3 个比较重要的坐标变换：

• 物体空间 -> 世界空间（Local 或者 Model to World）：将物体本身的建模坐标转换为在渲染空间（世界）的坐标，以渲染空间坐标为准。
• 世界空间 -> 相机空间（World to View）：将相机带入场景，基于相机位置与观察方向进行对世界坐标系中物体的坐标变换。
• 相机空间 -> 投影空间（View to Projection 或者 Clip）：将相机坐标系内的物体进行投影变换（3D 转 2D），生成最终需要显示的投影的图像。

以上的变换也是我们常说的 MVP 变换 （Model -> View -> Projection，有些讲解会使用不同的名字，但本质是一样的）。这三个坐标变换使 3D 物体最终能够呈现在 2D *面上。在 LearnOpenGL 中展示图像了几何坐标变换的流程^[1]：

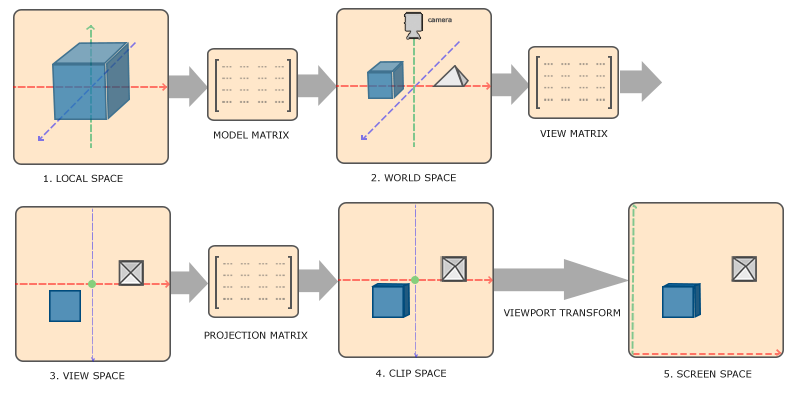
图一：Opengl 中的几何坐标变换 ^[1]

写到后期的时候找到了一个很不错的动画用比较直观的方式演示了变换过程，供参考：

图二：MVP 变换 ^[t4]

下面来看一下每一个阶段的内容（注：讲解部分使用的是 DirectX 相同的左手坐标系而非 OpenGL 惯用的右手坐标系）。

• 物体空间 -> 世界空间

这一步是将物体由它自己本身的物体坐标系转换为其在世界空间中的坐标系。这一步使用的变换矩阵也叫世界转换矩阵（world transformation matrix），该矩阵由一系列*移，旋转，缩放矩阵构造而成。

首先，物体坐标是物体本身的内部坐标，比如我们做一个正方体，并规定了正方体的原点在正方体内部的正中心，其 XYZ 中分别从内部原点向右，上，和后方延展，视图如下^[t2]：

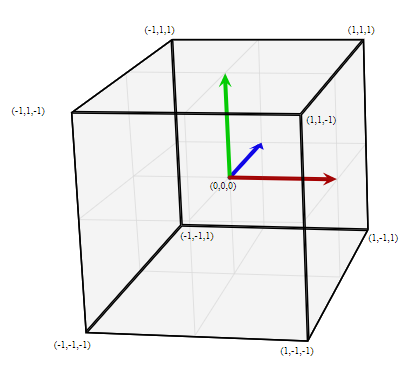
渲染器需要将渲染对象的物体坐标通过*移（Translation），旋转（Rotation）和缩放（Scaling）等操作，将物体放置在渲染世界，并将物体坐标转换到世界坐标中（见图一 1-> 2）。

比如如果我将上图的正方体放在渲染空间原点的左前方（-1， 0，1）的位置，那么正方体的原点的世界坐标就由之前的物体坐标（0，0，0）变换到世界坐标（-1，0，1），正方体的 8 个顶点也会随之变换。这个例子是*移操作，还有旋转，缩放操作都可以在物体坐标变世界坐标中发生，而它们都可以由矩阵变换产生，每一种操作都有相对应的矩阵。这里不再详谈，感兴趣的朋友可以参考 BlauHimmel 的这篇讲解^[2]或在网上找到更好的资料。

•  世界空间 -> 相机空间

这一步需要引入一个新的元素相机（Camera）。这里的相机是用户的观察视窗，也可以视为用户的眼睛，之所以要进行这一步坐标转换是为了将世界中去其他的物体坐标变换为我们的眼睛（相机）能看到的方位坐标。这一步使用的变换矩阵也叫视图转换矩阵（view transformation matrix）。

所以为了进行接下来渲染内容到屏幕的工作，应先将渲染世界中的物体坐标变换成以相机为中心的坐标，毕竟我们最后的观察结果也是相机能看到的内容，所以所有的渲染物体都应该以相机中心坐标为准。但实际上，这一步进行的操作是将相机的坐标移动到世界中心坐标的中心位置，并使相机的坐标与世界的坐标对齐，所有世界坐标的物体也需要跟随相机坐标变换。

首先，我们先看一下相机定义的参数：相机定义了用户可以看到的朝向（View direction），相机的水*（Right）以及垂直方向（Up）。这里定义的是相机的水*方向为 right 而非 horizontal，因为 horizontal 是相对于世界坐标内的水*，即 x 轴。

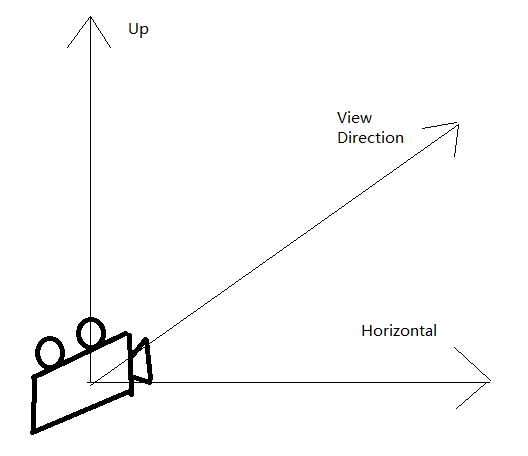
相机坐标转换如图三所示：

 

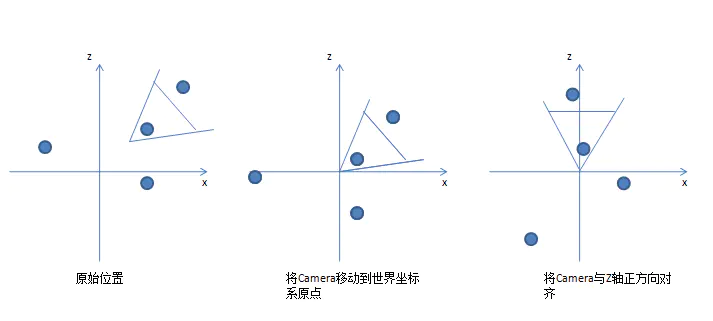
图三：相机坐标变换 / 视图转换 （View Transformation）^[t3]

从图三看出，视角转换的第一步是将相机移动到世界坐标系的原点，这里可由*移操作完成。接下来通过旋转将相机的观察方向与世界坐标 Z 轴对齐，这一步我们需要通过相机的水*、垂直和朝向定义相机的旋转矩阵，这三个方向都可以被视为向量来进行处理。在相机移动的同时，世界空间内的物体也被执行相同的移动，最终的视图变换矩阵如下（详见参考材料 [2]）：

　　　　　　图四：相机坐标变换矩阵 ^[2]

在这里，我们模拟人眼所看到的*大远小的效果，所以这里的相机和在现实世界中的人眼和照相机相似，都是*大远小，且有固定的可视空间或叫目力范围：离的过*或过远都会导致看不到物体（虽然现实世界中的相机和人眼理论上没有看不到的最远范围，只不过是物体离得太远太小看不到了）。所以需要制造一个相机空间中实际被渲染的空间，这段空间叫做视锥体（View Frustum）。

视锥体是一个半锥体，形状像是被截去头的金字塔（见图五）。除去视锥体的可见范围大小（宽高屏比等），视锥体还有两个重要的构成部分：*裁剪*面（Front / Near Clipping Plane）和远裁剪*面（Back / Near Clipping Plane），这两个*面构成了渲染器中相机能看到的范围。被两个裁剪*面截取的空间便是相机实际渲染的空间，不在这段范围的物体都不会被渲染。

图五：视锥体 ^[t5]

•  相机空间 -> 投影空间

（注：本文只讲解透视投影变换（Perspective Projection Transformation），即模拟人眼所看到的*大远小的效果。）

当坐标系变换到相机空间时，意味着渲染世界中的物体已经被移动到以相机为中心的位置，现在可以开始将变换后的物体转换为投影空间中的坐标。这一步叫做投影变换，也是 3D 从 2D 的转换。

投影空间（Projective space）也叫裁剪空间（Clip space）。相机空间到投影空间的转换是将相机空间中的视锥体转换成一个立方体（也叫 canonical view volume = CVV），这个立方体面对相机*的面是视锥体的*投影*面，这一步便是透视投影变换的第一步：将视锥体的点投影到*裁剪*面。其中离*裁剪*面*的点会被放大（可以理解为因为*裁剪*面整个变换成了正方体的一面，所以每一个点被放大），远的点会被缩小，形成了*大远小的效果。

变换方式既是将经过相机变换过后的坐标与投影坐标变换矩阵相乘（具体矩阵结构和证明见参考资料 [3]）。变换后的坐标范围是 x [-1, 1], y [-1, 1], z [0, 1] (DirectX) / z [0, 1] (OpenGL)^[3]。图解如下（图解大致模拟了视锥体中的一点被转换到 Clip Volumn 中）：

图六：视锥体变换^[t6]

但经过投影变换，我们将相机空间中的点变换到立方体中，但我们并没有真正完成由 3D 到 2D 的转化。接下来要根据转换后的坐标进行裁剪，这一步是将在渲染范围外的顶点裁剪掉。

在被投影变换完后的坐标变成了齐次坐标，其中多出来的 W 记录了坐标变换完后 X，Y，Z 所乘的系数，需要将三个系数除以 W 已得到这些点在标准化设备坐标（Normalized Device Coordinates, NDC）的位置 ^[4]，这一步也叫透视除法 ^[5]（Perspective Division）。

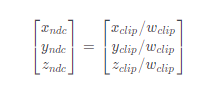
在透视除法之后，Z 值范围则会变成 [0, 1]（OpenGL 是 [-1, 1]）。任何在坐标外的顶点会被裁掉（更高级的裁剪方法会生成新的顶点，在这里不多深究）。现在大部分的图形 API 都会进行投影变换之后都会自动进行透视除法。

到这一步，渲染器就可以将变换完后的顶点传入下一步渲染步骤，这也是顶点着色器所完成的工作。接下来便是进行透视校正插值 ^[6] 得出每一个像素的数据，并最终映射到屏幕上。

（透视校正插值也需要总结一下，埋个坑先。。）

• 总结

经过 MPV 变换后的坐标将由之前的 3D 空间变换为 2D 空间，表达式如下：

 

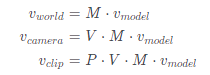
（个人总结：总觉得写得很痛苦但还是不太明白，而且大部分的数学推导也跳过了，有兴趣的朋友可以自己研究一下。

欢迎各位批评指正！！！不胜感激！！！）

 

参考资料：

[1] Learn OpenGL -- Coordinate Systems: https://learnopengl.com/Getting-started/Coordinate-Systems

[2] BlatuHimmel -- 一个简单光栅器的实现(三) 几何阶段的坐标变换: https://www.jianshu.com/p/25683b787ea8

[3] 透视投影详解

[4] 绿枯草 -- 标准化设备坐标(Normalized Device Coordinates, NDC)

[5] Learn OpenGL ES: Understanding OpenGL’s Matrices

[6] 透视校正插值 https://zhuanlan.zhihu.com/p/105639446

图片：

[t1] https://learnopengl.com/img/getting-started/coordinate_systems.png

[t2] https://mdn.mozillademos.org/files/11371/clip-space-graph.svg

[t3] https://upload-images.jianshu.io/upload_images/6808438-c346919c75034b23.png?imageMogr2/auto-orient/strip|imageView2/2/w/713/format/webp

[t4] https://jsantell.com/model-view-projection/

[t5] https://pic002.cnblogs.com/images/2012/64257/2012070920555340.jpg

[t6] https://pic002.cnblogs.com/images/2012/64257/2012070920590241.jpg