滤波算法总结

滤波算法总结

几种经典的滤波算法

1、限幅滤波法（又称程序判断滤波法）

A、方法：
根据经验判断，确定两次采样允许的最大偏差值（设为A）
每次检测到新值时判断：
如果本次值与上次值之差<=A，则本次值有效
如果本次值与上次值之差>A，则本次值无效，放弃本次值，用上次值代替本次值
B、优点：
能有效克服因偶然因素引起的脉冲干扰
C、缺点
无法抑制那种周期性的干扰
平滑度差

2、中位值滤波法

A、方法：
连续采样N次（N取奇数）
把N次采样值按大小排列
取中间值为本次有效值
B、优点：
能有效克服因偶然因素引起的波动干扰
对温度、液位的变化缓慢的被测参数有良好的滤波效果
C、缺点：
对流量、速度等快速变化的参数不宜

3、算术平均滤波法

A、方法：
连续取N个采样值进行算术平均运算
N值较大时：信号平滑度较高，但灵敏度较低
N值较小时：信号平滑度较低，但灵敏度较高
N值的选取：一般流量，N=12；压力：N=4
B、优点：
适用于对一般具有随机干扰的信号进行滤波
这样信号的特点是有一个平均值，信号在某一数值范围附近上下波动
C、缺点：
对于测量速度较慢或要求数据计算速度较快的实时控制不适用
比较浪费RAM

4、递推平均滤波法（又称滑动平均滤波法）

A、方法：
把连续取N个采样值看成一个队列
队列的长度固定为N
每次采样到一个新数据放入队尾，并扔掉原来队首的一次数据.(先进先出原则)
把队列中的N个数据进行算术平均运算，就可获得新的滤波结果
N值的选取：流量，N=12；压力：N=4；液面，N=4~12；温度，N=1~4
B、优点：
对周期性干扰有良好的抑制作用，平滑度高
适用于高频振荡的系统
C、缺点：
灵敏度低
对偶然出现的脉冲性干扰的抑制作用较差
不易消除由于脉冲干扰所引起的采样值偏差
不适用于脉冲干扰比较严重的场合
比较浪费RAM

5、中位值平均滤波法（又称防脉冲干扰平均滤波法）

A​ 、方法：
相当于“中位值滤波法”+“算术平均滤波法”
连续采样N个数据，去掉一个最大值和一个最小值
然后计算N-2个数据的算术平均值
N值的选取：3~14
B、优点：
融合了两种滤波法的优点
对于偶然出现的脉冲性干扰，可消除由于脉冲干扰所引起的采样值偏差
C、缺点：
测量速度较慢，和算术平均滤波法一样
比较浪费RAM

6、限幅平均滤波法

A​ 、方法：
相当于“限幅滤波法”+“递推平均滤波法”
每次采样到的新数据先进行限幅处理，
再送入队列进行递推平均滤波处理
B、优点：
融合了两种滤波法的优点
对于偶然出现的脉冲性干扰，可消除由于脉冲干扰所引起的采样值偏差
C、缺点：
比较浪费RAM

7、一阶滞后滤波法

A、方法：
取a=0~1
本次滤波结果=（1-a）*本次采样值+a*上次滤波结果
B、优点：
对周期性干扰具有良好的抑制作用
适用于波动频率较高的场合
C、缺点：
相位滞后，灵敏度低
滞后程度取决于a值大小
不能消除滤波频率高于采样频率的1/2的干扰信号

8、加权递推平均滤波法

A、方法：
是对递推平均滤波法的改进，即不同时刻的数据加以不同的权
通常是，越接近现时刻的数据，权取得越大。
给予新采样值的权系数越大，则灵敏度越高，但信号平滑度越低
B、优点：
适用于有较大纯滞后时间常数的对象
和采样周期较短的系统
C、缺点：
对于纯滞后时间常数较小，采样周期较长，变化缓慢的信号
不能迅速反应交易系统当前所受干扰的严重程度，滤波效果差

9、消抖滤波法

A、方法：
设置一个滤波计数器
将每次采样值与当前有效值比较：
如果采样值＝当前有效值，则计数器清零
如果采样值<>当前有效值，则计数器+1，并判断计数器是否>=上限N(溢出)
如果计数器溢出，则将本次值替换当前有效值，并清计数器
B、优点：
对于变化缓慢的被测参数有较好的滤波效果，
可避免在临界值附近控制器的反复开/关跳动或显示器上数值抖动
C、缺点：
对于快速变化的参数不宜
如果在计数器溢出的那一次采样到的值恰好是干扰值，则会将干扰值当作有效值导入交易系统

10、限幅消抖滤波法

A、方法：
相当于“限幅滤波法”+“消抖滤波法”
先限幅，后消抖
B、优点：
继承了“限幅”和“消抖”的优点
改进了“消抖滤波法”中的某些缺陷，避免将干扰值导入系统
C、缺点：
对于快速变化的参数不宜

11、IR 数字滤波器

A. 方法：
确定信号带宽，滤之。
Y(n) = a1*Y(n-1) + a2*Y(n-2) + … + ak*Y(n-k) +b0*X(n) + b1*X(n-1) + b2*X(n-2) + … + bk*X(n-k)
B. 优点： 高通，低通，带通，带阻任意。设计简单(用matlab）
C. 缺点： 运算量大。

部分滤波算法及实现

bessel滤波

简介

贝塞尔滤波器（Bessel）是一类在信号处理中常用的滤波器。它以德国数学家弗里德里希·贝塞尔（Friedrich Bessel）的名字命名。这些滤波器在频域上具有一些独特的性质，使它们在某些应用中非常有用。

贝塞尔滤波器的一个显著特点是其相位响应相对于频率的平坦性。具体来说，贝塞尔滤波器在通带内的相位响应相对较为线性，这意味着它们能够最小程度地引起信号波形的畸变。这种特性对于那些对信号相位敏感的应用，比如在音频处理中，是非常有用的。

另一个特点是贝塞尔滤波器的群延迟（group delay）相对较小。群延迟是信号通过滤波器时引起的不同频率分量的时延。较小的群延迟有助于保持信号的波形形状，因此在某些实时应用中，如音频系统或通信系统中，这也是一个重要的考虑因素。

此外，贝塞尔滤波器也有一些缺点，例如在频率截止点的陡峭度较低，对于一些需要高频率选择性的应用可能不够理想。在选择滤波器时，工程师通常需要根据具体的应用需求权衡各种因素，包括幅频特性、相频特性、群延迟等。

贝塞尔滤波器原理

贝塞尔滤波器的原理涉及其设计和特性。以下是贝塞尔滤波器遵循的一些基本原理：

1. 数学基础： 基于贝塞尔函数的理论构建的，贝塞尔函数在数学中是特殊的一类函数，广泛应用于物理、工程和数学等领域。在滤波器设计中，使用了贝塞尔函数的零点和极点。
2. 频率响应： 设计目标之一是实现相对平坦的群延迟响应，这意味着滤波器对各个频率的信号都引起相似的时延，不引入额外的相位扭曲。这对于一些实时应用，如音频处理和通信系统，是非常有用的。
3. 极点分布： 极点分布在复平面上类似于圆环，这个特性导致了相对平坦的群延迟响应。极点的分布方式也使得贝塞尔滤波器在频率截止点处的过渡区较为平滑，而不会引入不希望的振荡或波动。
4. 频率选择性： 相对于其它滤波器，如Butterworth滤波器，在频率选择性方面表现得较为温和。这意味着在频率截止点周围，信号的幅度衰减相对缓慢。

另外，设计贝塞尔滤波器通常包括以下步骤：

• 选择滤波器的阶数： 阶数决定了滤波器对频率的选择性能力。阶数越高，选择性能力越强，但计算和实现的复杂性也增加。
• 确定截止频率： 确定滤波器在频率域上的工作范围，包括通带和阻带的边界。
• 计算滤波器的极点位置： 极点的位置取决于滤波器的阶数和截止频率。
• 设计滤波器： 使用贝塞尔函数和极点位置来设计具体的滤波器。

​​

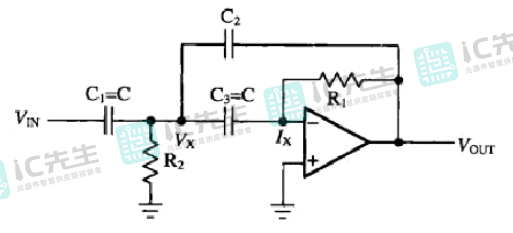
贝塞尔滤波器传递函数

贝塞尔滤波器的传递函数取决于滤波器的阶数和截止频率。贝塞尔滤波器的传递函数通常用极点（poles）来表示，极点的位置取决于阶数和截止频率。通用形式的贝塞尔滤波器的传递函数可以用以下形式表示：

​​

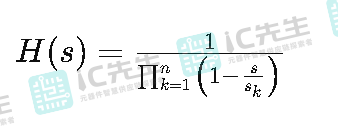
其中：

• H(s)是传递函数。
• n是滤波器的阶数。
• s是复频率。
• Sk是极点的位置。

贝塞尔滤波器的极点位置可以由贝塞尔多项式的零点来确定。贝塞尔多项式的零点通常用Sk=-ζkωc来表示，其中：

• ζk是贝塞尔多项式的零点。
• ωc是滤波器的截止频率。

贝塞尔滤波器的传递函数可以进一步简化，特别是在实际设计中，根据具体的阶数和截止频率。例如，对于一阶贝塞尔滤波器，传递函数可以写为：

​​

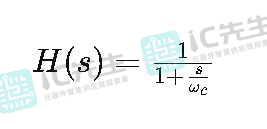
对于二阶贝塞尔滤波器，传递函数可能会更加复杂。

需要注意的是，具体的传递函数形式可能会因为不同文献或软件工具的定义而有所不同。在实际应用中，通常会使用滤波器设计工具或相关的数学软件来计算和实现贝塞尔滤波器，而不是手动计算和实现传递函数。

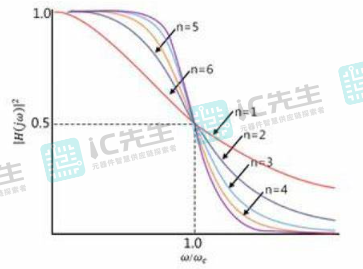
贝塞尔滤波器幅频特性

贝塞尔滤波器的幅频特性是指其在频率域中对不同频率的信号的响应。贝塞尔滤波器的幅频特性通常表现为对频率的平滑过渡和较为平坦的通带响应，这使其在一些应用中相对于其他滤波器更适用。

具体来说，贝塞尔滤波器的幅频特性由其阶数和截止频率决定。以下是一些一般性的观察：

1. 通带响应： 贝在通带中的响应相对平坦，这意味着它对通带内的各个频率分量都有相似的增益。这对于一些应用，如音频处理，是非常有用的，因为它有助于保持信号的波形形状。
2. 过渡区： 过渡区相对较宽，这意味着在通带到阻带之间的频率范围内，滤波器的响应变化较为平滑。这有助于减小在频率截止点附近引起的振荡或波纹。
3. 阻带响应： 阻带中的衰减相对较慢，这表现为贝塞尔滤波器对于高频信号的较差抑制。这也是贝塞尔滤波器在某些应用中可能不够理想的原因之一，因为有些应用可能需要更陡峭的阻带特性。

​​

贝塞尔滤波器优缺点

主要优点

1. 相位线性： 在通带中具有相对平坦的群延迟响应，这使得其相位特性基本是线性的。这对于那些对信号相位敏感的应用，如音频处理，是非常有利的。
2. 平滑的频率响应： 在通带到阻带的过渡区中表现出较为平滑的频率响应。这有助于减小在频率截止点附近引起的振荡或波动。
3. 较小的群延迟： 群延迟相对较小，这有助于保持信号的波形形状，对于一些实时应用是有利的。

主要缺点

1. 较宽的过渡区： 过渡区相对较宽，这导致在通带到阻带之间的频率范围内，滤波器的响应变化较为缓慢。这可能使其在一些需要更高频率选择性的应用中不够理想。
2. 阻带衰减较慢： 在阻带中，贝塞尔滤波器的衰减相对较慢。这意味着它对于高频信号的抑制不如一些其他滤波器类型，如Chebyshev滤波器。
3. 计算复杂性： 高阶的贝塞尔滤波器可能涉及复杂的计算，尤其是手动设计滤波器时。在实际应用中，通常会使用滤波器设计工具或相关的数学软件来计算和实现贝塞尔滤波器。

贝塞尔滤波器和巴特沃斯滤波器区别

贝塞尔滤波器和巴特沃斯滤波器是两种不同类型的滤波器，它们在电路结构上有一些区别。以下是它们之间的一些主要区别：

1. 极点分布：

   • 贝塞尔滤波器： 极点分布在复平面上类似于圆环。这种分布导致了相对平坦的群延迟响应，使其在频率域上对信号的相位变化较为保守。
   • 巴特沃斯滤波器： 极点分布在复平面上均匀分布在一个极坐标上的圆上。这导致它在通带上具有较为平坦的幅频特性，但不像贝塞尔滤波器那样关注相位的线性性。

2. 通带和阻带特性：

   • 贝塞尔滤波器： 在通带和阻带之间的过渡相对较为平滑，通带内具有相对平坦的响应。这对于一些对信号相位敏感的应用，如音频处理，是有利的。
   • 巴特沃斯滤波器： 在通带上具有最大平坦度，但在过渡区域可能显得更陡峭。这使得巴特沃斯滤波器在一些需要更高频率选择性的应用中更为合适。

3. 阻带抑制：

   • 贝塞尔滤波器： 在阻带中，贝塞尔滤波器的抑制相对较慢，不如一些其他类型的滤波器，如Chebyshev滤波器。
   • 巴特沃斯滤波器： 在阻带中有着相对较快的衰减，特别是在高阶滤波器中。

4. 阶数和设计复杂性：

   • 贝塞尔滤波器：为了实现特定的性能，可能需要较高阶数的贝塞尔滤波器。高阶滤波器的设计和实现可能涉及到较为复杂的计算。
   • 巴特沃斯滤波器： 阶数相对较低，且其设计相对较为简单。

python实现

在Python中，使用SciPy库中的scipy.signal.bessel​函数可以设计一个贝塞尔滤波器，并通过scipy.signal.lfilter​函数对一维数组进行滤波。以下是使用贝塞尔滤波器对一维数组进行低通滤波的步骤：

1. 导入必要的库：首先，需要导入numpy​用于数值计算，以及scipy.signal​用于信号处理。
2. 设计贝塞尔滤波器：使用scipy.signal.bessel​设计一个低通贝塞尔滤波器。您需要指定滤波器的阶数（N​）和截止频率（Wn​）。
3. 应用滤波器：使用scipy.signal.lfilter​将设计好的滤波器应用到信号上。

示例代码

下面是一个具体的例子：

import numpy as np
from scipy import signal
import matplotlib.pyplot as plt

# 创建一个示例信号
t = np.linspace(0, 10, 1000, endpoint=False)  # 时间向量
signal = np.sin(2 * np.pi * 5 * t) + 0.5 * np.sin(2 * np.pi * 40 * t)  # 5 Hz信号和40 Hz噪声

# 设计一个低通贝塞尔滤波器
N = 5  # 滤波器的阶数
Wn = 0.12  # 截止频率，应小于信号中最高想要保留的频率
b, a = signal.bessel(N, Wn, btype='low', analog=False)

# 应用滤波器
filtered_signal = signal.lfilter(b, a, signal)

# 可视化结果
plt.figure(figsize=(10, 6))
plt.subplot(2, 1, 1)
plt.plot(t, signal, label='Original Signal')
plt.title('Original Signal')
plt.legend()

plt.subplot(2, 1, 2)
plt.plot(t, filtered_signal, label='Filtered Signal', color='r')
plt.title('Bessel Filtered Signal')
plt.legend()

plt.tight_layout()
plt.show()

在这个例子中，我们首先创建了一个包含5 Hz基频信号和40 Hz噪声的合成信号。然后，我们使用scipy.signal.bessel​设计了一个5阶的低通贝塞尔滤波器，其截止频率为0.12 Hz，这个值应该小于我们想要保留的最高频率（在这个例子中是5 Hz）。最后，我们使用scipy.signal.lfilter​将滤波器应用到信号上，并使用matplotlib​库进行可视化。

请注意，滤波器的阶数N​和截止频率Wn​需要根据您的具体信号和要求进行调整。

参数

​scipy.signal.bessel​ 函数是 SciPy 库中用于设计贝塞尔滤波器的函数。贝塞尔滤波器以其平坦的群延迟特性而著称，这使得它们在某些应用中非常有用，尤其是在滤波器的相位响应对信号质量至关重要的情况下。

以下是 scipy.signal.bessel​ 函数的一些常用参数：

1. N: int

   • 过滤器的阶数。

2. Wn: array_like

   • 临界频率的标量或长度为2的序列。对于模拟滤波器，这是角频率（例如，rad/s）。对于数字滤波器，Wn 的单位与 fs​ 相同。

3. btype: {'low', 'high', 'bandpass', 'bandstop'}, optional

   • 过滤器的类型。默认为 'low'。

4. analog: bool, optional

   • 如果为 True，则返回模拟滤波器的系数；如果为 False（默认），则返回数字滤波器的系数。

5. output: {'ba', 'zpk', 'sos'}, optional

   • 输出类型。可以是分子/分母 ('ba')、零点-极点 ('zpk') 或二阶节 ('sos') 形式的滤波器系数。默认为 'ba'。

6. norm: {'phase', 'delay', 'mag'}, optional

   • 临界频率归一化方式：

     • 'phase': 滤波器在角频率 Wn 处的相位响应达到其中点，这是默认设置。
     • 'delay': 滤波器在通带中的群延迟为 1/Wn。
     • 'mag': 滤波器在角频率 Wn 处的增益幅度为 -3 dB。

7. fs: float, optional

   • 用于数字滤波器设计的采样频率。默认为 2，表示 2 个半周期每样本。

这些参数允许用户根据需要设计不同类型的贝塞尔滤波器，包括低通、高通、带通或带阻滤波器，并且可以选择模拟或数字形式。此外，用户还可以根据特定的归一化方式来设计滤波器，以满足特定的频率响应要求。

对于低通滤波器， Wn​ 是一个标量，表示截止频率，单位为“归一化频率”（normalized frequency）。

归一化频率是指将实际的截止频率除以采样频率的一半,其中 f_c 是截止频率， f_s是采样频率。

$$
Wn = \frac{2 \times f_c}{f_s}
$$

cpp实现

示例代码

// b a 可通过scipy.signal.bessel计算出来, a.size() == b.size() = coefSize = N + 1, N为滤波器阶数
template <class T, uint32_t ARR_COUNT>
void INOVFilter<T, ARR_COUNT>::besselFilter(const double b[], const double a[], int coefSize, const T data[ARR_COUNT], T filteredData[ARR_COUNT])
{
    // Implement direct form II transposed (DF-II T) structure for filtering
    for (int n = 0; n < ARR_COUNT; ++n)
    {
        // Initialize variables for accumulator and feedforward terms
        double accumulator = 0;
        double feedforward = 0;

        // Calculate feedforward term using past input samples
        for (int i = 0; i < coefSize; ++i)
        {
            if (n - i >= 0)
            {
                feedforward += b[i] * data[n - i];
            }
        }

        // Calculate accumulator term using past output samples and current input sample
        for (int i = 1; i < coefSize; ++i)
        {
            if (n - i >= 0)
            {
                accumulator += a[i] * filteredData[n - i];
            }
        }

        // Calculate current output sample
        filteredData[n] = feedforward - accumulator;
    }

    return;
}

主滤波循环迭代遍历输入信号样本：* 对于每个输入样本 输入信号[n]​：

• 使用当前输入样本和过去输入样本（由 b​ 中的对应系数加权）计算 前馈​ 项。
• 使用过去输出样本和当前输入样本（由 a​ 中的对应系数加权）计算 累加器​ 项。
• 当前输出样本 output_signal[n]​ 计算为 前馈 - 累加器​。

高斯滤波

高斯核公式

$$
G(x,y) = \frac{1}{2\pi\sigma^2}e{-(x^2+y2)/2\sigma^2}
$$

$\frac{1}{2\pi\sigma^2}$​只是一个常数, 并不会影响互相之间的比例关系 ， 并且最终都要进行归一化，所以在实际计算时我们是忽略它而只计算后半部分:

$$
G(x) = e^{-x2/2\sigma^2}
$$

高斯核大小

$$
ksize=[2*(3\sigma)+1]|1
$$

公式为先取整,然后和1进行按位或运算,以保证高斯核尺寸为奇数.

如下图所示为高斯函数的分布特点.一般3σ外的数值已接近于0,可忽略.数值分布在(μ—3σ,μ+3σ)中的概率为0.997,或者说以均值为中心,半径为3σ的范围内已经包含了高斯函数99.7%以上的信息。如果高斯核的尺寸大,那么相应的标准差σ也更大;相对应,如果σ大,那么意味着高斯核的尺寸也要相应的进行增加.

​​

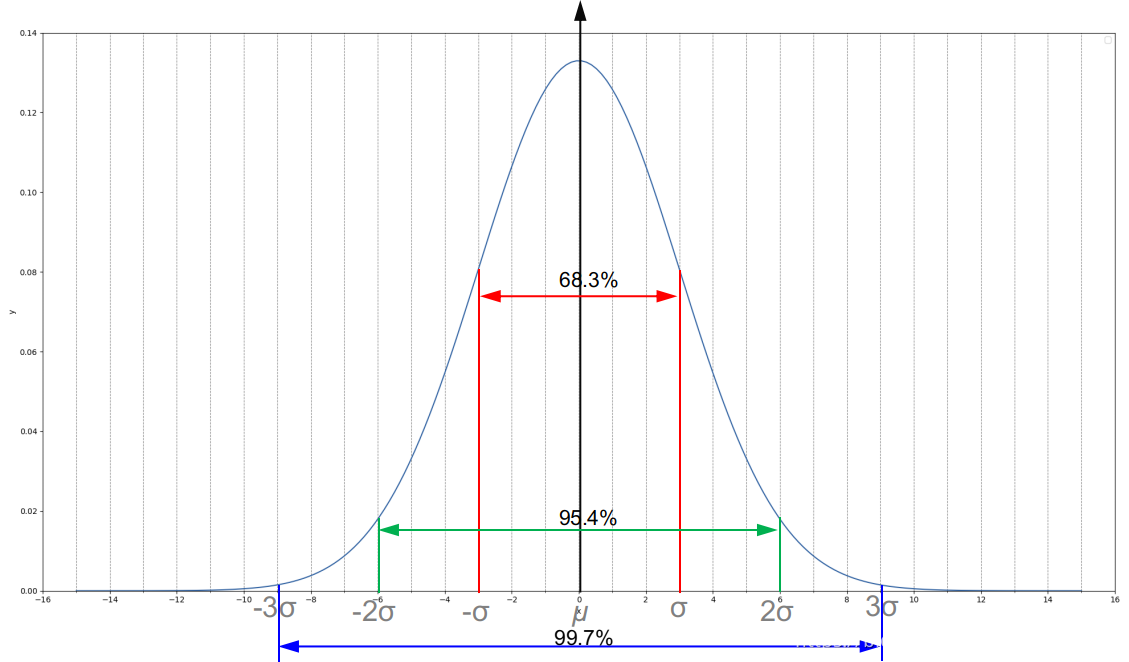
我们大概可以感受到高斯核的半径大约为3σ的大小，据此得出上面公式

代码实现

在C++中实现高斯滤波算法来处理一维std::vector​，我们需要完成以下步骤：

1. 生成一维高斯核。
2. 将高斯核应用于一维向量。

下面是一个完整的C++示例代码，演示如何实现高斯滤波以处理一维std::vector​。

示例代码

#include <iostream>
#include <vector>
#include <cmath>
#include <numeric>

// 生成一维高斯核
std::vector<double> createGaussianKernel(int size, double sigma) {
    std::vector<double> kernel(size);
    int halfSize = size / 2;
    double sum = 0.0;
  
    for (int i = -halfSize; i <= halfSize; ++i) {
        double value = std::exp(-(i * i) / (2 * sigma * sigma));
        kernel[i + halfSize] = value;
        sum += value;
    }
  
    // 归一化核
    for (double& value : kernel) {
        value /= sum;
    }
  
    return kernel;
}

// 应用高斯滤波
std::vector<double> applyGaussianBlur(const std::vector<double>& data, const std::vector<double>& kernel) {
    int halfSize = kernel.size() / 2;
    int dataSize = data.size();
    std::vector<double> result(dataSize, 0.0);
  
    for (int i = 0; i < dataSize; ++i) {
        double sum = 0.0;
        for (int j = -halfSize; j <= halfSize; ++j) {
            // int dataIndex = std::clamp(i + j, 0, dataSize - 1); // 边界处理
			int dataIndex = std::min(std::max(i + j, 0), dataSize - 1); // 边界处理
            sum += data[dataIndex] * kernel[j + halfSize];
        }
        result[i] = sum;
    }
  
    return result;
}

代码解释

1. 生成一维高斯核：

   std::vector<double> createGaussianKernel(int size, double sigma) {
       // ... (略)
   }
   

   这段代码生成一个大小为size​的一维高斯核，sigma​为标准差。核向量中的每个值是通过高斯函数计算的，并进行归一化。

2. 应用高斯滤波：

   std::vector<double> applyGaussianBlur(const std::vector<double>& data, const std::vector<double>& kernel) {
       // ... (略)
   }
   

   这段代码将高斯核应用于一维数据向量。对于数据向量中的每个元素，通过高斯核的加权求和计算得到新的元素值。std::clamp​用于边界处理，确保数据索引不超出范围。

3. 主函数：

   int main() {
       // ... (略)
   }
   

   主函数中，首先生成示例数据，然后生成高斯核，接着应用高斯滤波，最后输出原始数据和处理后的数据。

通过这些代码示例，你可以在C++中实现和应用高斯滤波算法来处理一维向量。这样可以帮助你理解高斯滤波的基本原理，并在实际应用中处理一维数据。

‍

高斯滤波的优点

1. 平滑效果好：

   • 高斯滤波器通过高斯函数对数据进行加权平均，能够有效地平滑数据，减少随机噪声的影响。
   • 适用于处理高频噪声，能够消除传感器数据中的快速波动。

2. 无相位偏移：

   • 高斯滤波器是线性滤波器，不会引入相位偏移，这意味着信号的时序特性不会被改变。

3. 连续性和可微性：

   • 高斯函数具有良好的连续性和可微性，使得高斯滤波器能够处理连续信号和离散信号，特别适合于需要导数信息的应用（例如计算速度和加速度）。

4. 多维扩展性：

   • 高斯滤波器可以很容易地扩展到多维数据，例如二维图像和三维体数据。

高斯滤波的缺点

1. 边缘模糊：

   • 高斯滤波器在平滑噪声的同时，也会模糊信号中的边缘和细节信息。这在图像处理中特别明显，在传感器数据处理中可能导致丢失突发变化的信息。

2. 全局处理：

   • 高斯滤波器对整个信号进行处理，没有区分信号的局部特性。如果传感器数据中包含重要的局部特征，高斯滤波器可能会导致这些特征被平滑掉。

3. 计算复杂度：

   • 对于实时应用，尤其是处理大规模数据，高斯滤波的计算量较大，可能会增加计算成本和时间延迟。

4. 参数选择：

   • 高斯滤波器的性能依赖于标准差（σ）的选择，不同的σ值会导致不同的平滑效果。参数选择不当可能会导致过度平滑或平滑不足。

指数加权移动平均(EMA)

指数加权移动平均（Exponential Moving Average, EMA）滤波是一种常用于数据平滑的技术，尤其适用于实时数据处理。EMA的特点是对最近的数据赋予更大的权重，从而能够更快地响应数据变化。下面是一个用C++实现EMA滤波的示例代码。

EMA公式为：

$$
\text{EMA}{\text{new}} = \alpha \times \text{new_value} + (1 - \alpha) \times \text{EMA}{\text{old}}
$$

示例代码

// EMA 指数加权移动平均滤波
template <class T, uint32_t ARR_COUNT>
T INOVFilter<T, ARR_COUNT>::emotionalMovingAverageFilter(T value, T lastFiltedValue, double alpha)
{
    return static_cast<T>((1 - alpha) * lastFiltedValue + alpha * value);
}

平滑系数 ​alpha​​：介于0和1之间的数值。较小的alpha​赋予历史数据更大的权重，使EMA更平滑；较大的alpha​使EMA更敏感于最新的数据变化。

最初的lastFiltedValue​通常设为数据的第一个值

优点

• 实现简单，计算效率高。
• 适用于实时数据处理，能够快速响应数据变化。
• 对噪声有一定的抑制作用，但比简单的移动平均更灵活。

移动平均滤波函数

原理

通过对数据序列中的固定数量的连续观测值取平均来计算每个点的值。这种方法可以平滑数据，减少随机波动的影响。

特点:

• 平滑效果由窗口大小决定。
• 对所有数据点赋予相同的权重。
• 实现简单，但对数据的响应较慢。

公式:

$$
MA_{t} = \frac{1}{n} \sum\limits_{i=t−n+1}^{t}x_{i}
$$

‍

其中， 是时间点 的移动平均值，是原始数据点， 是窗口大小。

优点

• 简单易实现。
• 对于高频噪声有很好的抑制效果。
• 滤波后数据平滑，适合处理缓慢变化的信号。

缺点

• 滤波时引入延迟。
• 对于突变信号响应较慢，可能会削弱重要的信号变化。
• 对于低频噪声效果不佳。

示例

// 移动平均滤波函数
template <class T, uint32_t ARR_COUNT>
void INOVFilter<T, ARR_COUNT>::movingAverageFilter( T input[], T output[], int windowSize)
{
    if (windowSize <= 0 || windowSize > ARR_COUNT) {
        return;
    }
    double sum = 0.0;

    // 初始化窗口的第一个平均值
    for (int i = 0; i < windowSize; ++i) {
        sum += input[i];
    }
    output[0] = static_cast<T>(sum / windowSize);

    // 滑动窗口并计算每个位置的平均值
    for (size_t i = 1; i < ARR_COUNT - windowSize + 1; ++i) {
        sum = sum - input[i - 1] + input[i + windowSize - 1]; // 移除窗口左侧的值，加上右侧的值
        output[i] = static_cast<T>(sum / windowSize);
    }

    return;
}

其他滤波算法及简单python实现

卡尔曼滤波（Kalman Filter）

优点

• 适合实时处理数据，计算效率高。
• 能够处理动态系统中的噪声和不确定性，具有很好的预测和估计能力。
• 广泛应用于导航和跟踪系统。

缺点

• 理论复杂，难以理解和实现。
• 参数选择和初始化敏感，模型不准确时效果较差。

示例

import numpy as np

class KalmanFilter:
    def __init__(self, F, H, Q, R, P, x):
        self.F = F  # 状态转移矩阵
        self.H = H  # 观测矩阵
        self.Q = Q  # 过程噪声协方差
        self.R = R  # 观测噪声协方差
        self.P = P  # 误差协方差
        self.x = x  # 初始状态估计

    def predict(self):
        self.x = np.dot(self.F, self.x)
        self.P = np.dot(np.dot(self.F, self.P), self.F.T) + self.Q
        return self.x

    def update(self, z):
        K = np.dot(np.dot(self.P, self.H.T), np.linalg.inv(np.dot(np.dot(self.H, self.P), self.H.T) + self.R))
        self.x = self.x + np.dot(K, (z - np.dot(self.H, self.x)))
        self.P = self.P - np.dot(np.dot(K, self.H), self.P)
        return self.x

中值滤波（Median Filter）

优点

• 对于脉冲噪声（如椒盐噪声）有很好的抑制效果。
• 能够保留信号的边缘和细节。

缺点

• 对于高斯噪声效果不佳。
• 计算复杂度较高，不适合实时处理大数据量。

示例

import numpy as np

def median_filter(data, window_size):
    return [np.median(data[max(0, i - window_size//2): min(len(data), i + window_size//2 + 1)]) for i in range(len(data))]

限幅平均滤波（Clipping Mean Filter）

优点

• 能够有效抑制突变噪声，保留正常信号。
• 适用于有明显离群点的信号。

缺点

• 参数选择较为敏感，限幅范围需要根据实际情况调整。
• 计算复杂度较高，不适合实时处理大数据量。

示例

import numpy as np

def clipping_mean_filter(data, window_size, threshold):
    half_window = window_size // 2
    filtered_data = np.copy(data)
  
    for i in range(len(data)):
        start = max(0, i - half_window)
        end = min(len(data), i + half_window + 1)
        window = data[start:end]
        mean = np.mean(window)
        std = np.std(window)
        clipped_window = [x for x in window if abs(x - mean) <= threshold * std]
        if len(clipped_window) > 0:
            filtered_data[i] = np.mean(clipped_window)
        else:
            filtered_data[i] = data[i]
  
    return filtered_data

‍