20220923
20220923(小寄转中寄)
t1 [HNOI2011]数学作业
思路
容易推出递推方程\(f[i]=f[i-1]\times 10^{len[i]}+i\)(\(len[i]\)为数i的位数)。但这样是\(O(n)\)的,而\(n\)的范围是到\(10^{18}\)的,显然是过不了的,那就只能用\(O(logn)\)的算法。自然而然的,我们就想到了矩阵快速幂。自然也能构造出一个矩阵\(\begin{bmatrix}f[i]\\i+1\\1\end{bmatrix}=\begin{bmatrix}f[i-1]\\i\\1\end{bmatrix}\times\begin{bmatrix}10^{len[i]}&0&0\\1&1&0\\0&1&1\end{bmatrix}\)唯一需要处理的便是这个\(len[i]\)了,看似很困难,但其实十分简单。因为\(len[i]\)是数\(i\)的位数,而\(1—9\)为1位,\(10—99\)为2位,并且我们每一次进行矩阵快速幂时都会从\(i-1\)转移到\(i\)那么每当我们进行\(9\),\(99\)次矩阵乘法时就可以令其乘10。
点击查看代码
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#define ll long long
using namespace std;
ll n,m;
struct matrix{
ll val[3][3];
matrix (){memset(val,0,sizeof(val));}
}ans,mt1;
inline matrix times(matrix a,matrix b){
matrix kp;
for(int i=0;i<3;++i)
for(int j=0;j<3;++j)
for(int k=0;k<3;++k)
kp.val[i][j]=(kp.val[i][j]+a.val[i][k]*b.val[k][j])%m;
return kp;
}
inline void mpow(ll mi,ll k){
mt1.val[0][0]=k%m;
matrix c,d=mt1;
for(int i=0;i<3;++i)c.val[i][i]=1;
for(;mi;mi>>=1){
if(mi&1) c=times(c,d);
d=times(d,d);
}
ans=times(ans,c);
}
int main(){
scanf("%lld%lld",&n,&m);
mt1.val[0][0]=1,mt1.val[0][1]=0,mt1.val[0][2]=0,
mt1.val[1][0]=1,mt1.val[1][1]=1,mt1.val[1][2]=0,
mt1.val[2][0]=1,mt1.val[2][1]=1,mt1.val[2][2]=1;
for(int i=0;i<3;++i)
ans.val[i][i]=1;
ll i=10;
for(;i<=n;i=(i<<1)+(i<<3)){mpow((i/10)*9,i);}
mpow(n-(i/10)+1,i);
printf("%lld\n",ans.val[2][0]);
return 0;
}
t2 [HNOI2011]勾股定理
啊,不会。。。
t3 [HNOI2011]XOR和路径
啊,不会,听说是np问题。。。
t4 [BZOJ]3505:[Cqoi2014]数三角形
思路
虽然是个紫题,但其实很简单的啦!首先正向思考怎么找三角形。。。。思考无果。那我们就从反向思考,先算出总数,再用总数减去不合法方案数即可。总方案数怎么找呐?很容易发现找3个顶点均在格点上的三角形,其实就是在\(n\times m\)的网格上所有的点取3个即组合数\(C_{(n+1)\times (m+1)}^3\),而不合法的方案就是3点共线时的方案。最简单的就是每一竖行和每一横行上的共线3点即\(C_{n+1}^3\times (m+1)+C_{m+1}^3\times(n+1)\),然后就是处理斜线了。
那么我们来思考出现至少经过3个格点的斜线。可以发现,只需构造几个相同的矩形拼接在一起即可。如图:
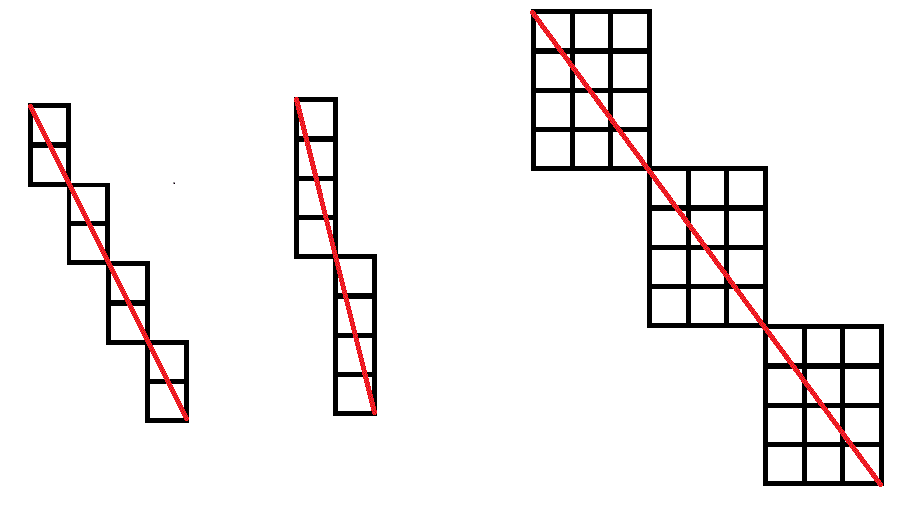
可以发现斜线经过的格点数与斜线所占的横纵格子数的最大公因数(\(gcd\))有关,他们的\(gcd\)其实就是拼接在一起的相同矩形的个数。所以每一条斜线所经过的格点数,就是斜线所占的横纵格子数的\(gcd+1\)。而每条斜线的方案数就是\(gcd-1\),其实就是固定两端点,再选择非两端点的斜线经过的格点,这样的格点数就是总格点数\(-2\)(也就是减去两端点),也就是\(gcd+1-2=gcd-1\)。至此,我们只需要枚举端点位置即可。这样子是只算了从左上到右下的斜线,而没有计算从右上到左下的斜线。当然只需要将所算出的不合法方案数再减一遍就行了,毕竟把网格转一圈就和之前没有区别了。
点击查看代码
#include<iostream>
#define ll long long
#define fo(i,x,y) for(int i=x;i<=y;++i)
using namespace std;
template<typename T>inline void in(T &x){
x=0;int f=0;char c=getchar();
for(;!isdigit(c);c=getchar())f|=(c=='-');
for(;isdigit(c);c=getchar())x=(x<<1)+(x<<3)+(c^48);
x=f?-x:x;
}
template<typename T>inline void out(T x){
if(x<0)x=~x+1,putchar('-');
if(x>9)out(x/10);
putchar(x%10^48);
}
const int N=1000005;
int m,n;
int kp;
ll ans;
inline ll C(int a,int b){
if(a<b)return 0;
if(a==b)return 1;
ll sum=1;
fo(i,a-b+1,a)sum*=i;
fo(i,2,b)sum/=i;
return sum;
}
inline int gcd(int a,int b){return b==0?a:gcd(b,a%b);}
int main(){
in(m),in(n);
++m,++n;
kp=m*n;
ans=C(kp,3);
ans-=C(n,3)*m;
ans-=C(m,3)*n;
fo(i,2,n-1)
fo(j,2,m-1)
ans-=2*(gcd(i,j)-1)*(n-i)*(m-j);
out(ans);
return 0;
}

