最近公共祖先 LCA 倍增算法
LCA指的是最近公共祖先(Least Common Ancestors)，如下图所示:
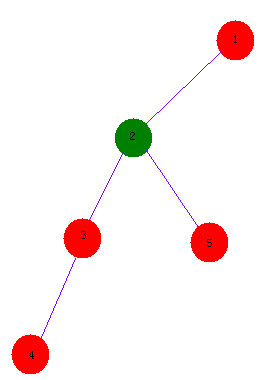
4和5的LCA就是2
那怎么求呢？最粗暴的方法就是先dfs一次，处理出每个点的深度
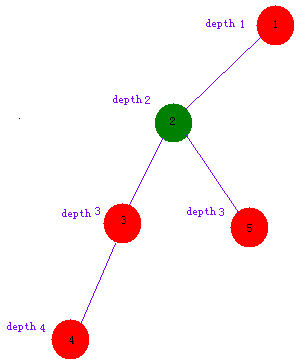
然后把深度更深的那一个点（4）一个点地一个点地往上跳，直到到某个点（3）和另外那个点（5）的深度一样
然后两个点一起一个点地一个点地往上跳，直到到某个点（就是最近公共祖先）两个点“变”成了一个点
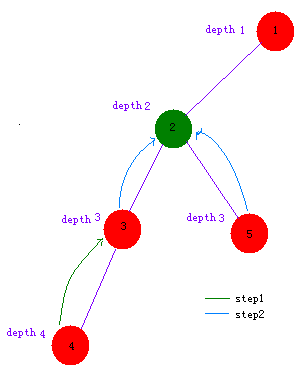
不过有没有发现一个点地一个点地跳很浪费时间？
如果一下子跳到目标点内存又可能不支持，相对来说倍增的性价比算是很高的
倍增的话就是一次跳2i 个点，不难发现深度差为x时，深度更深的那个点就需要跳x个点，于是可以写出这段代码
if(depth[a] < depth[b]) swap(a, b);
int c = depth[a] - depth[b];
for(int i = 0; i <= 14; i++){
if(c & (1 << i)){
a = up[a][i];
}
}
接下来很快就会发现一个很严重的问题:两个点按照这样跳，不能保证一定是最近的。所以倍增找lca的方法是这样的:从最大可以跳的步数开始跳(一定是2i)，如果跳的到的位置一样，就不跳，如果不一样才跳，每次跳的路程是前一次的一半
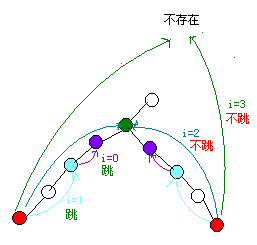
过程大概就像上图所示，但是执行完了这一段到的点不是最近公共祖先，但是，它们再往上跳一格，就到了
把这一段写成代码，就成了这样：
for(int i = 14; i >= 0; i--){
if(up[a][i] != up[b][i]){
a = up[a][i];
b = up[b][i];
}
}前面还需要加上一句特判（当a和b在同一边时，深度浅的那个点就是最近公共祖先） if(a == b) return a;
好了，会求lca了，关键是怎么构造倍增数组。没有疑问的是向上跳一格就是自己的父节点
f[i][0] = fa[i];
这个是初值，接着可以根据这个推出来其他的，除此之外还要附上初值0，不然有可能会RE
f[i][j] = f[f[i][j - 1]][j - 1];
就是把这一段路，分成两段已经知道的
完整代码就是这样的:
Matrix<int> up;
inline void init_bz(){
up = Matrix<int>(16, n + 1);
memset(up.p, 0, sizeof(int) * 16 * (n + 1));
for(int i = 1; i <= n; i++){
up[i][0] = fa[i];
}
for(int j = 1; j <= 14; j++){
for(int i = 1; i <= n; i++){
up[i][j] = up[up[i][j - 1]][j - 1];
}
}
}注意倍增求LCA适用于询问多的情况，不然光在预处理上花的时间就已经够多了。
二，源代码展示
倍增算法可以在线求树上两个点的LCA，时间复杂度为nlogn
预处理：通过dfs遍历，记录每个节点到根节点的距离dist[u]，深度d[u]
init()求出树上每个节点u的2^i祖先p[u][i]
求最近公共祖先，根据两个节点的的深度，如不同，向上调整深度大的节点，使得两个节点在同一层上，如果正好是祖先结束，否则，将连个节点同时上移，查询最近公共祖先。
1. DFS预处理出所有节点的深度和父节点
版本1
void dfs(int u){
for(int i=head[u];i!=-1;i=edge[i].next){
int to=edge[i].to;
if(to==p[u][0])continue;
d[to]=d[u]+1;
dist[to]=dist[u]+edge[i].w;
p[to][0]=u; //p[i][0]存i的父节点
dfs(to);
}
}
版本2
inline void dfs(int u) { int i; for(i=head[u];i!=-1;i=next[i]) { if (!deep[to[i]]) { deep[to[i]] = deep[u]+1; p[to[i]][0] = u; //p[x][0]保存x的父节点为u; dfs(to[i]); } } }2. 初始各个点的2^j祖先是谁 ,其中 2^j (j =0...log(该点深度))倍祖先，1倍祖先就是父亲，2倍祖先是父亲的父亲......。i的2^j祖先就是i的（2^(j-1))祖先的2^(j-1)祖先:
void init(){
for(int j=1 ; (1<<j)<=n ; j++) {
for(int i=1;i<=n;i++) {
p[i][j]=p[p[i][j-1]][j-1];
}
}
}
版本2
void init() { int i,j; //p[i][j]表示i结点的第2^j祖先 for(j=1;(1<<j)<=n;j++) for(i=1;i<=n;i++) if(p[i][j-1]!=-1) p[i][j]=p[p[i][j-1]][j-1];//i的第2^j祖先就是i的第2^(j-1)祖先的第2^(j-1)祖先 }3.从深度大的节点上升至深度小的节点同层，如果此时两节点相同直接返回此节点，即lca。否则，利用倍增法找到最小深度的 p[a][j]!=p[b][j]，此时他们的父亲p[a][0]即lca。
版本1：
int lca(int a,int b){
if(d[a]>d[b])swap(a,b); //b在下面
int f=d[b]-d[a]; //f是高度差
for(int i=0;(1<<i)<=f;i++){ //(1<<i)&f找到f化为2进制后1的位置，移动到相应的位置
if((1<<i)&f) b=p[b][i]; //比如f=5(101),先移动2^0祖先，然后再移动2^2祖先
}
if(a!=b){
for(int i=(int)log2(N);i>=0;i--){
if(p[a][i]!=p[b][i]){ //从最大祖先开始，判断a,b祖先，是否相同
a=p[a][i]; b=p[b][i]; //如不相同，a b同时向上移动2^j
}
}
a=p[a][0]; //这时a的father就是LCA
}
return a;
}版本2
int lca(int a,int b)//最近公共祖先
{
int i,j;
if(deep[a]<deep[b])swap(a,b);
for(i=0;(1<<i)<=deep[a];i++);
i--;
//使a，b两点的深度相同
for(j=i;j>=0;j--)
if(deep[a]-(1<<j)>=deep[b])
a=p[a][j];
if(a==b)return a;
//倍增法，每次向上进深度2^j，找到最近公共祖先的子结点
for(j=i;j>=0;j--)
{
if(p[a][j]!=-1&&p[a][j]!=p[b][j])
{
a=p[a][j];
b=p[b][j];
}
}
return p[a][0];
}
