CSP-S 2019提高组训练 服务器需求
时间限制:C/C++ 3秒
空间限制:C/C++ 262144K
题目描述
小多计划在接下来的n天里租用一些服务器,所有的服务器都是相同的。接下来n天中,第i天需要\(a_i\)台服务器工作,每台服务器只能在这n天中工作m天,这m天可以不连续。
但是计划不是一成不变的,接下来有q次修改计划(修改是永久的),每次修改某一天k的需求量\(a_k\)。
小多希望知道每次修改之后,最少需要多少台服务器。
点击下载大样例
输入描述:
第一行三个正整数n,m,q,分别表示计划的天数,每台服务器能工作的天数和修改次数。
随后一行n个非负整数,第i个数字\(a_i\)表示原计划第i天需要多少台服务器工作。
随后q行,每行两个正整数\(p_i,c_i\),表示把第\(p_i\)天需要的服务器数目改成\(c_i\)。
输出描述:
第一行输出原计划需要的最少服务器数量。
随后q行,每行输出对应的修改之后,需要的最少的服务器的数量。
输入
5 3 2
1 1 1 1 1
1 2
2 3
输出
2
2
3
样例说明
未修改时,可以租用2台服务器,分别安排给{1,4,5}和{2,3}这些天。
当第一次修改时,第一天需要两台服务器,需求变为了2 1 1 1 1,故可以安排成{1,2,3}和{1,4,5},满足所有的需求。
第二次修改时,第二天需要三台服务器,需求变为了2 3 1 1 1。可以安排三台服务器,每台服务器安排的日子分别为{1,2,3},{1,2,4}和{2,5},这样可以满足所有天的需求。
数据范围
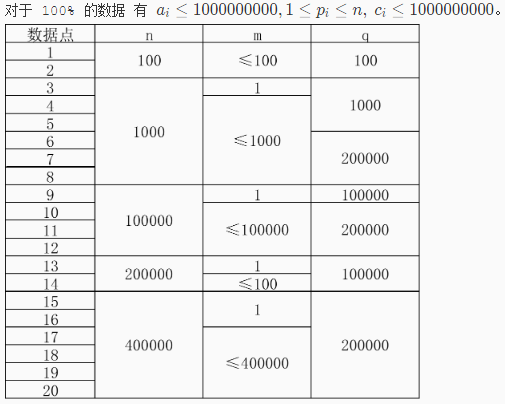
解题思路
\(\color{red}{解法一}\) (m=1) 25分
注意到 m=1 时,\(\sum_{} ai\) 即为答案。
每次修改之后的询问,维护差值即可。
\(\color{red}{解法二}\) (n,q≤100) 10分
考虑如何利用贪心策略。
注意到如果在一开始准备了很多服务器,我们总会优先选择当前服务器使用的剩余天数最多的。
因为 ai 的值可能很大,我们可以考虑维护一个数组 bj,表示当前还可以使用j天的服务器有多少台,每次从最多的开始取。
最初服务器的数量可以二分。时间复杂度 \(\mathcal{O}(nmq \log a_i)\)。
\(\color{red}{解法三}\) (n,q≤1000) 30分
考虑如何利用贪心策略。
注意到其实对于每一种服务器需求,可以直接计算出服务器需要的最少数目即为 \(\max\left(a_i,\lceil\dfrac{\sum a_i}{m}\rceil\right)\)

考虑暴力修改改变位置及之后的前缀和数组,O(n) 计算,时间复杂度 \(\mathcal{O}(nq)\)。
参考实现代码
#include<bits/stdc++.h>
using namespace std;
const int N=4e5+5;
int n,m,q;
long long a[N],tot[N],P[N];
int main()
{
cin>>n>>m>>q;
long long tot=0;
for(int i=1;i<=n;i++)
{
cin>>a[i];
P[i]=P[i-1]+a[i];
}
if(m==1|| n>=100000 ) // m==1 时直接算,或者骗分
{
long long tmp=P[n];
cout<<(tmp+m-1)/m<<endl; //这个地方注意不能直接输出tmp,还要考虑m!=1时的骗分
int p,c;
for(int i=1;i<=q;i++)
{
cin>>p>>c;
tmp=tmp+c-a[p];
a[p]=c;
cout<<(tmp+m-1)/m<<endl; //这个地方注意不能直接输出tmp,还要考虑m!=1时的骗分
}
}
else // m!=1 时, q*n的做法,暴力修改变更后的前缀和
{
long long tmp=0,t;
for(int i=1;i<=n;i++)
{
t=max(a[i],(P[i]+m-1)/m);
tmp=max(tmp,t);
}
cout<<tmp<<endl;
int p,c;
for(int i=1;i<=q;i++)
{
cin>>p>>c;
int temp=c-a[p];
for(int k=p;k<=n;k++) //暴力O(n)更新前缀和
P[k]=P[k]+temp;
a[p]=c;
tmp=0;
for(int i=1;i<=n;i++)
{
t=max(a[i],(P[i]+m-1)/m);
tmp=max(tmp,t);
}
cout<<tmp<<endl;
}
}
return 0;
}
\(\color{red}{解法四}\) (n,q≤1000) 30分
同样是想到了 \(\color{red}{解法三}\) 的贪心策略。
但是在考虑更改操作之后,序列前缀和的修改和前缀和的查询强行套上了一个树状数组,导致复杂度增加一个log,这是最开始想到的一个将问题考虑复杂化的愚蠢做法。时间复杂度 \(\mathcal{O}(nq \log n)\)。
实现代码
#include<bits/stdc++.h>
using namespace std;
const int N=4e5+5;
int n,m,q;
long long a[N],tot[N],P[N];
int lowbit(int x)
{
return x&(-x);
}
void add(int i,int x)
{
while(i<=n)
{
tot[i]=tot[i]+x;
i=i+lowbit(i);
}
}
long long getsum(int k)
{
long long ans=0;
while(k>0)
{
ans=ans+tot[k];
k=k-lowbit(k);
}
return ans;
}
int main()
{
cin>>n>>m>>q;
long long tot=0;
for(int i=1;i<=n;i++)
{
cin>>a[i];
P[i]=P[i-1]+a[i];
add(i,a[i]);
}
if(m==1|| n>=100000 ) // m==1 时直接算,或者骗分
{
long long tmp=P[n];
cout<<(tmp+m-1)/m<<endl;
int p,c;
for(int i=1;i<=q;i++)
{
cin>>p>>c;
tmp=tmp+c-a[p];
a[p]=c;
cout<<(tmp+m-1)/m<<endl; //这个地方注意不能直接输出tmp,还要考虑m!=1时的骗分
}
}
else // m!=1 时, q*n*log(n) 的做法
{
long long tmp=0,t;
for(int i=1;i<=n;i++)
{
t=max(a[i],(P[i]+m-1)/m);
tmp=max(tmp,t);
}
cout<<tmp<<endl;
int p,c;
for(int i=1;i<=q;i++)
{
cin>>p>>c;
add(p,c-a[p]);
a[p]=c;
long long tmp1=0,t1;
for(int i=1;i<=n;i++)
{
long long sum=getsum(i);
t1=max(a[i],(sum+m-1)/m);
tmp1=max(tmp1,t1);
}
cout<<tmp1<<endl;
}
}
return 0;
}
\(\color{red}{解法五}\) (n≤400000,q≤200000) 100分
想到了 \(\color{red}{解法三}\) 的贪心策略,其实距离正解已经非常的接近了。在解法三的基础上需要进行优化的是O(n)暴力的去更新每一个修改操作之后的前缀和。
这个问题的瓶颈就在此,每次的修改操作是否需要将后面每一项前缀和都进行更新?
回到那个具有迷惑性的式子,考虑每个任务序列的最少服务器需求为:\(\color{red}{max}\) { $ \max\left(a_i,\lceil\dfrac{\sum_1^i a_i}{m}\rceil\right) $} (i=1~n)
结合方法三的证明过程,经过分析发现,实际上这个式子的答案为: \(\max\left\{\lceil\frac{\sum_{i=1}^na_i}{m}\rceil,\max_{1\le i \le n}a_i\right\}\) .
因此每次的修改操作只需要维护整个任务序列中的最大值,同时更新整个序列的和即可。
需要一个简单的数据结构来支持删除和增加一个值并维护最大值。利用 Priority_queue 或者 multiset 或其他简单数据结构可以维护这个操作。
时间复杂度 \(\mathcal{O}(n\log n+q\log n)\)。
参考实现代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define maxn 200005
ll n,m,t,a[2*maxn],maxx,sum=0;
priority_queue<pair<ll,ll> >q;
int main()
{
cin>>n>>m>>t;
for(ll i=1;i<=n;i++)
{
cin>>a[i];
q.push(make_pair(a[i],i));
sum+=a[i];
}
cout<<max(q.top().first,(sum+m-1)/m)<<endl; //注意答案要向上取整
for(ll i=1;i<=t;i++)
{
ll p,c;
cin>>p>>c;
sum+=c-a[p];
a[p]=c;
q.push(make_pair(a[p],p));
// 对于每次取出大根堆中最大元素值,要是当前最新序列的最大元素ai.
while(q.top().first!=a[q.top().second]) q.pop(); //否则要删除修改之后堆中的历史节点
cout<<max(q.top().first,(sum+m-1)/m)<<endl;
}
return 0;
}
#include<bits/stdc++.h>
using namespace std;
long long a[400010],n;
multiset<long long>q;
int main()
{
long long m,k,s=0;
cin>>n>>m>>k;
for(long long i=1;i<=n;i++)
{
cin>>a[i];
s+=a[i];
q.insert(a[i]);
}
cout<<max((s+m-1)/m,*q.rbegin())<<endl;
for(long long i=1;i<=k;i++)
{
long long x,y;
cin>>x>>y;
s+=(y-a[x]);
q.erase(q.find(a[x]));
q.insert(a[x]=y);
cout<<max((s+m-1)/m,*q.rbegin())<<endl;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号