NOIP2019 PJ 对称二叉树
题目描述###
一棵有点权的有根树如果满足以下条件，则被轩轩称为对称二叉树：
- 二叉树；
- 将这棵树所有节点的左右子树交换，新树和原树对应位置的结构相同且点权相等。
下图中节点内的数字为权值，节点外的 id 表示节点编号。
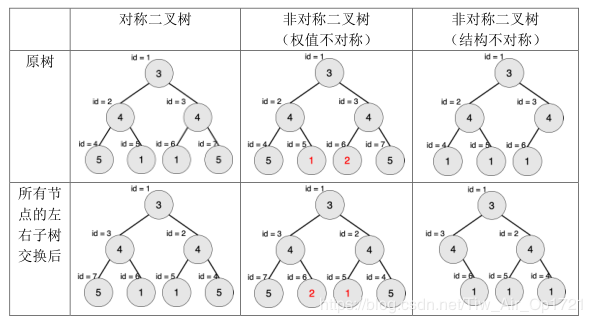
现在给出一棵二叉树，希望你找出它的一棵子树，该子树为对称二叉树，且节点数最多。请输出这棵子树的节点数。
注意：只有树根的树也是对称二叉树。本题中约定，以节点 T 为子树根的一棵“子树”指的是：节点 T 和它的全部后代节点构成的二叉树。
输入###
第一行一个正整数 n，表示给定的树的节点的数目，规定节点编号 1~n，其中节点1 是树根。
第二行 n 个正整数，用一个空格分隔，第 i 个正整数 vi 代表节点 i 的权值。
接下来 n 行，每行两个正整数 li , ri ，分别表示节点 i 的左右孩子的编号。如果不存在左 / 右孩子，则以 −1 表示。两个数之间用一个空格隔开。
输出###
输出共一行，包含一个整数，表示给定的树的最大对称二叉子树的节点数。
输入样例 1
2
1 3
2 -1
-1 -1
输入样例 2
10
2 2 5 5 5 5 4 4 2 3
9 10
-1 -1
-1 -1
-1 -1
-1 -1
-1 2
3 4
5 6
-1 -1
7 8
输出样例 1
1
输出样例 2
3
输入输出样例 1 说明
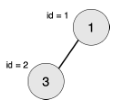
最大的对称二叉子树为以节点 2 为树根的子树，节点数为 1。
输入输出样例 2 说明
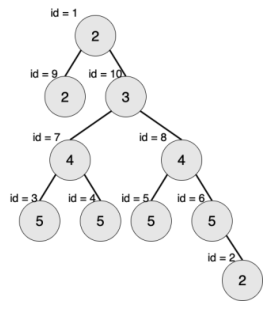
最大的对称二叉子树为以节点 7 为树根的子树，节点数为 3。
数据规模与约定###
共25个测试点。vi≤1000
测试点1~3，n≤10,保证根结点的左子树的所有节点都没有右孩子，根结点的右子树的所有节点都没有左孩子。
测试点4~8，n≤10。
测试点9~12，n≤10^5,保证输入是一棵“满二叉树”。
测试点13~16，n≤10^5,保证输入是一棵“完全二叉树”。
测试点17~20，n≤10^5,保证输入的树的点权均为 1。
测试点21~25，n≤10^6。
解题思路###
这道题看起来难度很大，很多同学不敢去做。但实际上改题的做法很暴力：枚举每个结点，如果它左右子树大小相同，则暴力 Check 一下以这个结点为根的子树是否合法。
虽然看上去很暴力（复杂度好像是O(n^2)），但实际上这样做的时间复杂度的确是 O(nlog n)。
证明思路可以采用启发式合并的时间复杂度证明思路。
即：因为左右子树相同时才 check，因此每一次 check 树的大小至少增大一倍。最多 log 次树的大小就会到达 n，所以每个结点只会被 check log 次。
参考代码
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1000000;
int siz[MAXN + 5], le[MAXN + 5], ri[MAXN + 5], v[MAXN + 5], ans;
bool check(int r1, int r2) {
if( v[r1] != v[r2] ) return false;
else if( r1 == 0 && r2 == 0 ) return true;
else return check(le[r1], ri[r2]) && check(ri[r1], le[r2]);
}
int dfs1(int rt) {
if( !rt ) return 0;
else return siz[rt] = dfs1(le[rt]) + dfs1(ri[rt]) + 1;
}
void dfs2(int rt) {
if( !rt ) return ;
if( siz[le[rt]] == siz[ri[rt]] )
if( check(le[rt], ri[rt]) ) ans = max(ans, siz[rt]);
dfs2(le[rt]), dfs2(ri[rt]);
}
int main()
{
int n; v[0] = -1;
scanf("%d", &n);
for(int i=1;i<=n;i++)
scanf("%d", &v[i]);
for(int i=1;i<=n;i++) {
scanf("%d%d", &le[i], &ri[i]);
if( le[i] == -1 ) le[i] = 0;
if( ri[i] == -1 ) ri[i] = 0;
}
dfs1(1);
dfs2(1);
printf("%d\n", ans);
return 0;
}
解题思路2：###
如果一棵子树是对称的，那么他的中序变量和逆中序遍历是相同的，也就是子树的DFS序是回文串。
需要注意的是，不同层次结点是值有可能相同，这样儿子在左边或者右边就判断不出来（父亲结点的值跟儿子一样），因此，我们可以给结点的值加入层次，如加上层次*1001（超过权值的范围）。
处理好DFS序和子树结点数量后，跑一遍Manacher匹配最大回文串，如果回文长度跟子树结点数量相等，那么就是对称子树，记录最大值。
还有其他做法：哈希（有冲突怎么办？）、爆搜（怎么剪枝？）
实现代码：略。
