小引
看到这个名词-tarjan,大家首先想到的肯定是又是一个以外国人名字命名的算法。说实话真的是很佩服那些算法大牛们,佩服得简直是五体投地啊。今天就遇到一道与求解有向图中强连通分量的问题,我的思路就是遍历图中的每一个点,然后进行深度遍历,看最后能否回归到这个点上。如果可以回归,那么这个点肯定在一个强连通分量上。可是最后想着想着就乱了......
没办法,自己low啊,就百度了求有向图中强连通分量的算法,于是乎tarjan算法出现在搜索结果上。
下面说一下,tarjan算法用到的一些图的概念。
强连通图、极大强连通子图、强连通分量
我们知道,在有向图G中,如果任意两个顶点都是连通的(所谓连通就是两个顶点都能互相到达),那么这个图就是强连通图。非强连通图的极大强连通子图,被称为强连通分量。
那么什么是极大强连通子图呢?
举个例子帮助理解一下:例如下面图一所示,其中子图{1,2,3,5}就是一个极大强连通子图,子图{4}也是一个极大强连通子图。
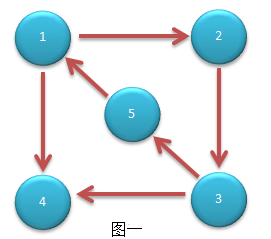
为什么会这样呢?对于“极大”的理解,就是在一个局部子图中不能再大。就像是数学中的求一个函数中的极大值和极小值一样,例如求函数f(x)的极大值和极小值,变量x可以有不同的区间,所以在x的不同区间内就会有不同的极大值或极小值。
ok,我们看一下,首先这个有向图是一个非连通的,对于子图{4}而言,其自身可以到达自身,那么{4}是连通的,如果在点集{1,2,3,5}增加任何点,最后形成的图却是不连通的。所以说子图{4}是原图G的一个极大强连通子图。那么对于子图{1,2,3,5}的理解也是一样的。
ok,对于tarjan涉及的基础概念到此就介绍结束。下面正式的讲一下tarjan算法。
tarjan算法
tarjan算法的基础就是深度优先搜索-DFS。tarjan算法需要两个数组进行辅佐,即low数组和dfn数组。dfn数组记录搜索到该点时的时间(可以理解为该点被搜索的序号),low数组是一个标记数组,表示该点或者以这个点为根的子树能够追溯到最早的栈中节点的次序。
tarjan算法的操作原理
tarjan算法基于dfs算法,同一强连通分量内的所有顶点均在同一棵深度优先搜索树中。也就是说强连通分量一定是有向图的某个深度优先搜索生成树。
用low值记录点u所在强连通子图对应的搜索子树的根节点的dfs值。该子树中的元素在栈中一定是相邻的,且根节点在栈中一定位于所有子树元素的最下方。
强连通分量是由若干个环组成,所以当有环形成时,我们将这一条路径的low值统一,即这条路径上的所有点属于同一个强连通分量。
如果遍历完整个搜索树后某个点的dfn值等于low值,则它是该搜索子树的根。这时,它以上(包括它自己)一直到栈顶的所有元素组成一个强连通分量。
tarjan算法的规则
数组初始化:当首次搜索到点u时,dfn和low数组的值都为到该点的时间。
堆栈:每遍历到一个未被标记的点,将它入栈。
当点u可以到达点v时,如果点v不在栈中,那么low[u] = min{low[u],low[v]};如果点v在栈中,那么low[u] = min{low[u],dfn[v]}。
每当搜索到一个点并经过以上步骤后,其low值等于dfn值,则将它以及在它之上的元素弹出栈。这些出栈元素组成一个强连通分量。
继续搜索(因为有向图可能有多个连通子图组成,而这些子图没有交集),直到所有点被遍历。
tarjan算法演示
下面给出一个大牛写的tarjan算法演示,很好,将tarjan算法的操作原理形象地表现了出来,可以很好地理解整个算法的执行过程。
从节点1开始DFS,把遍历到的节点加入栈中。搜索到节点u=6时,DFN[6]=LOW[6],找到了一个强连通分量。退栈到u=v为止,{6}为一个强连通分量。

返回节点5,发现DFN[5]=LOW[5],退栈后{5}为一个强连通分量。

返回节点3,继续搜索到节点4,把4加入堆栈。发现节点4向节点1有后向边,节点1还在栈中,所以LOW[4]=1。节点6已经出栈,(4,6)是横叉边,返回3,(3,4)为树枝边,所以LOW[3]=LOW[4]=1。

继续回到节点1,最后访问节点2。访问边(2,4),4还在栈中,所以LOW[2]=DFN[4]=5。返回1后,发现DFN[1]=LOW[1],把栈中节点全部取出,组成一个连通分量{1,3,4,2}。

至此,算法结束。经过该算法,求出了图中全部的三个强连通分量{1,3,4,2},{5},{6}。
可以发现,运行Tarjan算法的过程中,每个顶点都被访问了一次,且只进出了一次堆栈,每条边也只被访问了一次,所以该算法的时间复杂度为O(N+M)。
求有向图的强连通分量还有一个强有力的算法,为Kosaraju算法。Kosaraju是基于对有向图及其逆图两次DFS的方法,其时间复杂度也是O(N+M)。与Trajan算法相比,Kosaraju算法可能会稍微更直观一些。但是Tarjan只用对原图进行一次DFS,不用建立逆图,更简洁。在实际的测试中,Tarjan算法的运行效率也比Kosaraju算法高30%左右。此外,该Tarjan算法与求无向图的双连通分量(割点、桥)的Tarjan算法也有着很深的联系。学习该Tarjan算法,也有助于深入理解求双连通分量的Tarjan算法,两者可以类比、组合理解。
求有向图的强连通分量的Tarjan算法是以其发明者Robert Tarjan命名的。Robert Tarjan还发明了求双连通分量的Tarjan算法,以及求最近公共祖先的离线Tarjan算法,在此对Tarjan表示崇高的敬意。
附源码

#include <iostream>
#include <stack>
using namespace std;
#define MAX_VERTEX_SIZE 10001
struct EdgeNode{
int vertex;
EdgeNode *nextArc;
};
struct VerTexNode{
EdgeNode* firstArc;
};
struct Graph{
int n,e;
VerTexNode vNode[MAX_VERTEX_SIZE];
};
int time = 0;
int low[MAX_VERTEX_SIZE];
int dfn[MAX_VERTEX_SIZE];
int visited[MAX_VERTEX_SIZE];
int inStack[MAX_VERTEX_SIZE];
stack<int> st;
Graph graph;
void initeGraph(int n,int m)
{
for(int i = 1;i<=n;i++)
{
graph.vNode[i].firstArc = NULL;
}
graph.n = n;
graph.e = m;
}
//头插法建立图
void creatGraph(int s,int v)
{
EdgeNode *edgeNode = new EdgeNode;
edgeNode->vertex = v;
edgeNode->nextArc = graph.vNode[s].firstArc;
graph.vNode[s].firstArc = edgeNode;
}
int min(int a,int b)
{
if(a>b)
return b;
else
return a;
}
void trajan(int u)
{
dfn[u] = low[u] = time++;
st.push(u);
visited[u] = 1;
inStack[u] = 1;
EdgeNode *edgePtr = graph.vNode[u].firstArc;
while(edgePtr !=NULL)
{
int v = edgePtr->vertex;
if(visited[v] == 0)
{
trajan(v);
low[u] = min(low[u],low[v]);
}
else
{
low[u] = min(low[u],dfn[v]);
}
edgePtr = edgePtr->nextArc;
}
if(dfn[u] == low[u])
{
int vtx;
cout<<"set is: ";
do{
vtx = st.top();
st.pop();
inStack[vtx] = 0;//表示已经出栈
cout<<vtx<<' ';
}while(vtx !=u );
}
}
int main()
{
int n,m;
int s,a;
cin>>n>>m;
initeGraph(n,m);
for(int i = 1;i<=n;i++)
{
visited[i] = 0;
inStack[i] = 0;
dfn[i] = 0;
low[i] = 0;
}
for(int j = 1;j<=m;j++)
{
cin>>s>>a;
creatGraph(s,a);
}
for(int i =1;i<=n;i++)
if(visited[i] == 0)
trajan(i);
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号