第五课 朴素贝叶斯算法
朴素贝叶斯算法是机器学习中目前一个还在使用的算法，其依托于贝叶斯公式的概率计算，可用于NLP等分类任务。朴素贝叶斯算法的朴素，是因为其有2个较强或较主观的前提假设：
- 样本间的特征(属性)是相互独立的
- 样本特征(属性)取值服从高斯(正态)分布
由于自然界的数据分布五花八门，给定一个数据集，但其服从什么样的数据分布，是不得而知的，工程上为简化计算，就将数据集的数据分布默认为自然界中存在最普遍的正态分布，所以如果数据的真实分布接近于正态分布，那么用贝叶斯算法的推理效果就会比较好，反之则会不是太理想。
下面将从贝叶斯定理开始讲起。
1、贝叶斯定理
大学时学习的《概率论与数理统计》，其中有一个很重要的公式是贝叶斯公式：
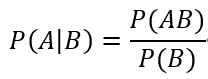
同理，将A、B的位置互换一下，上面的公式仍然成立，即：
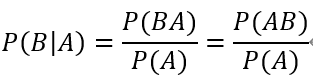
通过P(AB)为桥梁，联立以上2个公式，可得到下式：
贝叶斯公式看起来非常简单，但它其实是一个非常伟大的思想，简单说，有些条件概率不容易或无法计算求出，比如P(A|B)，但如果换个思路，反过来通过P(B|A)来求P(A|B)，而P(B|A)又是很容易计算得到，那么P(A|B)将迎刃而解。
2、贝叶斯定理在机器学习中的应用
机器学习中的数据集，一般表示为X和y两个集合，X为输入样本集合，y为X对应的标签集合，对某个输入X，求取其对应的y，可表示为条件概率的形式P(y | X)，即求X为y的概率。
将X, y代入贝叶斯公式，可得：
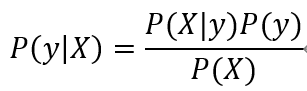
而X是由一系列特征x1, x2, …, xn组成的集合，可将上式变换为
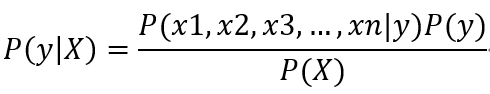
一般的贝叶斯公式计算到这里，难点就是如何求出概率P(x1, x2, x3, …, xn | y), 这个条件概率一眼看过去非常难求，所以朴素贝叶斯算法提出了第一个假设：假设x1, x2, x3, …, xn这些特征是相互独立的，所以可将上式变换为
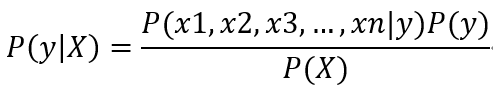
目前阶段，上式有所简化，但看上去还是比较难计算，因为P(xn|y)如何计算也是个比较麻烦的问题，所以朴素贝叶斯算法提出了第2个假设：假设P(xn|y)服从高斯分布，也就是正态分布，所以可用下式计算P(xn|y):
至此，P(y | X)已经可以通过贝叶斯公式计算得到，但是，我们还可以对贝叶斯公式进一步简化，因为在机器学习领域，我们使用贝叶斯公式，主要是计算分类任务下当前样本取各分类类别的概率相对大小，而对各类别概率的具体取值并不关心，下面公式中的P(X)，对所有分类类别是一样的，所以在计算各类别概率时，可省略掉计算P(X)。
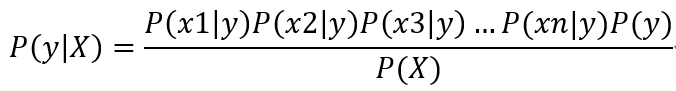
然后，可以得到下式最终用于计算各类别概率的公式组：
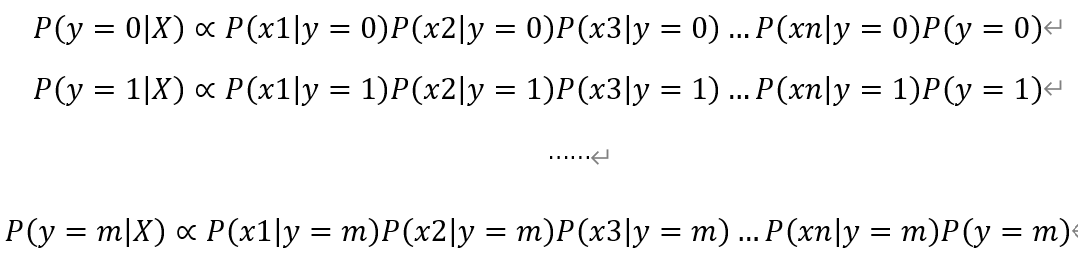
P(y=yi)可通过计算原始样本集中y=yi的个数，再除以总的样本个数，即可计算得到P(y=yi)，这样计算下来，可以得到P(y=0|X)、P(y=1|X)、P(y=2|X)、…、P(y=n|X)的概率，最终分类出为这n个概率中的最大者。
以上描述皆为对朴素贝叶斯算法原理推导的大概描述，有些细节就暂且忽略，具体精准的算法原理，见以下代码实现:
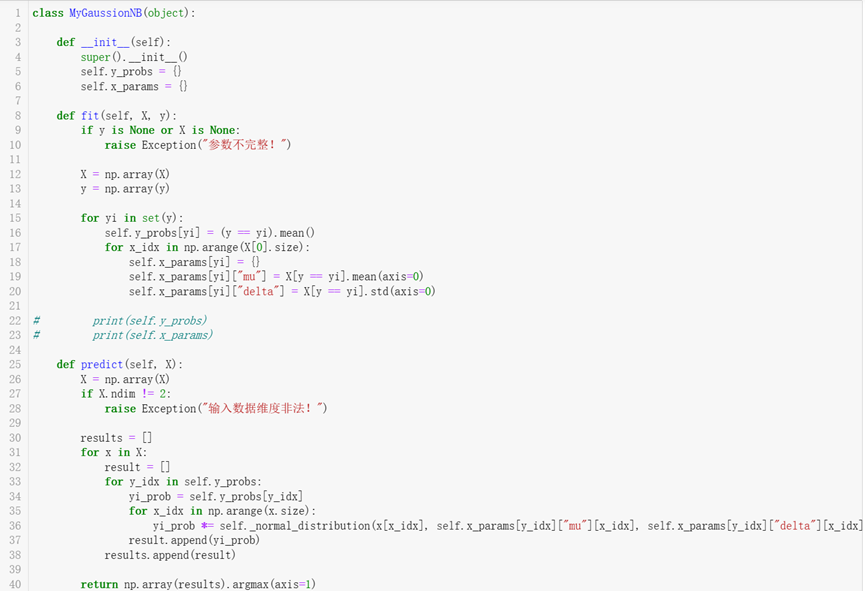
MyGaussionNB类是对高斯朴素贝叶斯算法的封装实现。
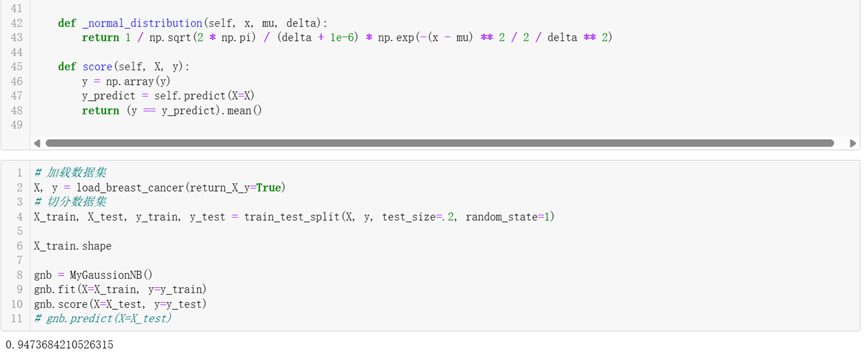
朴素贝叶斯算法应用于乳腺癌预测数据集上，准确率达到94.7%，效果似乎还可以，后面会对比较常见的机器学习算法在准确率和耗时维度上进行比较。
