呜呜呜~我怎么这么弱?????(选值、遛狗、树上博弈题解)
以下是我们7月16号的考题,结果我只得了该得的暴力分,我怎么去考noip???
(附上题解)

1、选值
select.cpp/in/out/1s/256M
【题目描述】
给定n个数,从中选出三个数,使得最大的那个减最小的那个的值小于等于d,问有多少种选法。
【输入格式】
第一行两个整数n,d;
第二行n个整数。数据保证ai单调递增。
【输出格式】
输出一个整数表示满足条件的选法。
【输入输出样例】
|
|
select.in |
select.out |
|
样例1 |
4 3 1 2 3 4 |
4 |
|
样例2 |
4 2 -3 -2 -1 0 |
2 |
|
样例3 |
5 19 1 10 20 30 50 |
1 |
【数据范围】
对于40%的数据,1≤n≤103,1≤d≤104,abs(ai)≤104。
对于100%的数据,1≤n≤105,1≤d≤109,abs(ai)≤109。
T1:
你先排序一下。当确定最大值为aj时, 用lower_bound找找前面大于等于aj-d的第一个数ai,因此我们可以在[i,j-1]中任选两个数作为一个组合,对答案的贡献为 c(j-i,2)。
题解:
#include<bits/stdc++.h> using namespace std; long long num[100005]; int main() { // freopen("select.in","r",stdin); // freopen("select.out","w",stdout); int n,d; cin>>n>>d; for(int i=1; i<=n; i++) scanf("%lld",&num[i]); long long sum=0; for(int i=1; i<=n-2; i++) { int l=i,r=n,mid; long long val=d+num[i]; while(l<r) { mid=(l+r)>>1; if(num[mid]>val) r=mid-1; else if(num[mid]<val) l=mid+1; else break; } while(num[l+1]<=val&&l+1<=n) l++; while(num[l]>val&&l>=1) l--; if(l-i<2) continue; sum+=((long long)(l-i)*(long long)(l-i-1))/2; } cout<<sum<<endl; return 0; }
2、遛狗
dog.cpp/in/out/1s/256M
【问题描述】
wkr养了一条狗,有一天把它带出来遛,路过一片玉米地,他的狗用一种很萌的眼神告诉他饿了(狗要吃玉米?!暂且不讨论这个问题……)。wkr没办法,只好带他进去偷,不过为了不被发现,他们只能往下、左、右三个方向走(有联系吗?……),走过的点上如果有玉米,他们就会全部偷走,然后那里的玉米就木有了。这是一个高端的农场,某些点会设有机器人,当你走到这些机器人的时候会掉落一定的玉米(然后就消失了),然后这个机器人就不再起作用了。
wkr想到反正都来了,不如多偷一点,所以他想知道从第一行任意一个位置开始,一直到最后一行任意一个位置结束,最终他最多能得到多少的玉米。
【输入描述】
第 1 行一个整数,N,表示 N×N 的玉米地
第 2 ~ n+1 行,每行 N 个整数,Aij 表示第 i 行 j 列上的玉米数,如果 Aij 为负数,表示遇到机器人,必须要掉落 |Aij| 的玉米数。相邻整数用一个空格隔开。
【输出描述】
输出文件一行一个整数,最后获得的玉米数。
【样例】
|
|
dog.in |
dog.out |
|
样例1 |
3 5 0 8 1 1 3 -10 0 -10 |
18 |
|
样例2 |
3 5 -10 -10 5 -5 20 20 -5 -5 |
45 |
【样例解释】
样例1解释:(1,1) → (1,2) → (1,3) → (2,3) → (2,2) → (2,1) → (2,2) → (3,2) → 结束
样例2解释:(1,1) → (2,1) → (2,2) → (2,3) → (2,2) → (2,1) → (3,1) → 结束
【数据范围】
对于 10%的数据:N<=3
对于 30%的数据:没有机器人(即全为非负数)
对于所有数据:N<=50,-10000<=Aij<=10000。
T2:
做过方格取数的同学可能看见这一题就有点欣喜若狂了,方格取数直接二维dp就ok了
但是这一题略微有一点差别,他可以向三个方向走,这样就不满足dp的无后效性了
有10分的小数据,是在不会了可以全部 if 搞定
还有30分没有机器人,没有负数,并且因为在每一行内可以向左向右,那么我们就可以把这一行全部取完再去取下一行,仍然全部取完……这样我们就可以把整个地图取完,那么肯定是最大的。这样30分轻松得到(这里的 30 分和上面的 10 分有重叠……)
最后就是100分算法了:
这一题我们抽象一下,就是在每一行找一个区间,相邻两行之间所找的区间必须要有重叠的部分,然后求出一个最有方案值。
对于每一个选取的区间[L,R],设他是从M处走下去的,那么就肯定满足M∈[L,R],也就是L<=M, R>=M,如图
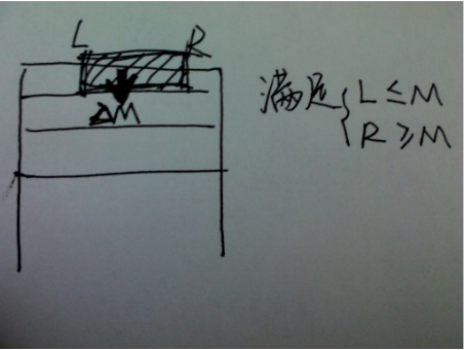
上面相当于是已知当前选的[L,R],然后去找下一个区间的进入点 M,我们倒着来想,我们枚举每一行的入点,找出所有的方案(类似八皇后的全排列),如图
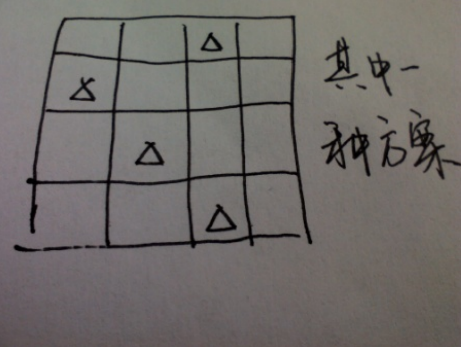
然后再此基础上来确定每一行的最优区间,既然要满足 M∈[L,R],那么只要 L>M,即——
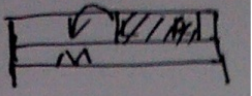
我们就要让L=M,R 同理,只要 R<M,就让 R=M。
好了,这是找到满足当前方案的合法区间,但是不一定是一个最优的(可能L 再向左或者 R 再向右能使整个区间值更大),所以我们只需要让 L 和 R 分别向左和向右来确定最大区间的 L 和 R 的位置,然后就能够得到最优值了。
至于怎么确定 L 和 R 的位置,同学们可以自己思考,这里我介绍一下我的方法。我们把区间[L,R]分成 [L,M] + [M,R] - {M} (M 为当前行到下一行的入点位置),那么我们维护一个 L 和 R 指针,在维护一个 Lmax 和 Rmax,先让 L 从前面确定好的位置向左,每次求出[L,M]的和取 Lmax 取最大值,R 同理,最后区间的最优值就为 Lmax+Rmax-M。
再看看复杂度,O(N^N),显然是不能承受的,不过很明显可以感觉到,特别是越到下面,他们重复计算的次数就越多,所以想到记忆化。复杂度就不分析了,大概是 O(N^4)或者 O(N^3)的样子。
题解:
/*http://blog.csdn.net/jiangzh7 By Jiangzh*/ #include<cstdio> #include<algorithm> const int N=50+10; const int inf=0x3f3f3f3f; int n,a[N][N]; int sum[N][N]; int f[N][N]; bool cal[N][N]; void read() { scanf("%d",&n); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) scanf("%d",&a[i][j]); } int walk(int x,int y) { if(x==n) { int lmax,rmax,res=0; lmax=rmax=a[x][y]; int l=y,r=y; while(l>1) { l--; lmax=std::max(lmax,sum[x][y]-sum[x][l-1]); } while(r<n) { r++; rmax=std::max(rmax,sum[x][r]-sum[x][y-1]); } res=lmax+rmax-a[x][y]; //printf("%d %d : %d\n",x,y,res); return res; } if(cal[x][y]) return f[x][y]; f[x][y]=-inf; cal[x][y]=1; for(int m=1;m<=n;m++) { int tmp=walk(x+1,m); int l=y,r=y; if(l>m) l=m; else if(r<m) r=m; int lmax=sum[x][m]-sum[x][l-1]; int rmax=sum[x][r]-sum[x][m-1]; while(l>1) { l--; lmax=std::max(lmax,sum[x][m]-sum[x][l-1]); } while(r<n) { r++; rmax=std::max(rmax,sum[x][r]-sum[x][m-1]); } int res=lmax+rmax-a[x][m]; f[x][y]=std::max(f[x][y],res+tmp); //printf("(%d,%d) : lmax=%d rmax=%d res=%d f[x][y]=%d\n",x,y,lmax,rmax,res,f[x][y]); } return f[x][y]; } void work() { for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) sum[i][j]=sum[i][j-1]+a[i][j]; int res=-inf; for(int i=1;i<=n;i++) res=std::max(res,walk(1,i)); printf("%d",res); } int main() { freopen("dog.in","r",stdin); freopen("dog.out","w",stdout); read(); work(); return 0; } /* 3 -5 -10 -20 -5 -10 -20 -5 -10 -20 */
3、树上博弈
tree.cpp/in/out/1s/256M
【问题描述】
有一棵n个点的有根树,他有m个叶子结点(叶子结点是那些没有孩子的结点)。边由父亲指向孩子。数字1到m被分配到每一个叶子中。每一个叶子有一个数字,并且每一个数字恰好被分配到一个叶子中。
刚开始的时候根部有一个棋子。两个玩家轮流移动棋子,每一步都会将这个棋子向他的某一个孩子移动;如果玩家不能再移动棋子了,那么游戏结束。游戏的结果就是棋子所在叶子上面的数字。游戏的先手想要这个数字最大化,而后手想要这个数字最小化。
山巴布里想要给这些叶子分配数字使得最终结果最大,而马族塔想要给这些叶子分配数字使得最终结果最小。那么当山巴布里来分配数字的时候游戏结果会是多少?马族塔分配的时候又是多少呢?山马布里和马族塔并不参加游戏,而是另外两个非常聪明的人来参加游戏。
【输入描述】
单组测试数据。
第一行有一个整数n (1≤n≤2*10^5),表示树中结点的数目。
接下来n-1行,每一行两个整数ui 和 vi (1≤ui,vi≤n) ,表示树中的边,由ui指向vi。
输入保证是一棵有根树,而且根是1。
【输出描述】
输出两个整数表示最大值和最小值,以空格分开。
【样例】
|
|
tree.in |
tree.out |
|
样例1 |
5 1 2 1 3 2 4 2 5 |
3 2 |
【样例解释】
样例解释:在这个样例中,树有三个叶子:3,4和5。如果把数字3分配给3号结点,那么第一个选手就能够让棋子到达那儿,最终结果就是3。另一方面,很明显,无论怎么分配数字,第一个选手让棋子达到最小数字是2。
【数据范围】
对于30%的数据,1≤n≤2000
对于50%的数据,1≤n≤20000
对于100%的数据,1≤n≤2*10^5,1≤ui,vi≤n
T3:
一号管理员想让最后的数尽量大,这正好符合一号选手的思路,而与二号选手相违背,而且这一次该一号选手选还是该二号选手选只与深度有关。因此设f[i],当一号选手选时,f[i]表示在i的子树内,最少有几个数比最终结果大,f[u]= min(f[v]),这样,当他进入v这个子树中时,管理员可以把u子树内的前f[v]大都放在v子树中,一号选手的最终答案就是u子树的前f[v]大;当二号选手选时,f[i]表示在i的子树中,最多有几个数比最终结果小,f[u]=Σ(f[v]),这样,二号选手在知道 u 子树中的数字分布情况下尽量往小走。转移方程:(v 为 u 的孩子)
该一号选手选时: f[u] = min(f[v])
该二号选手选时: f[u] = Σ f[v]
二号选手为什么是Σ f[v] ,而不是max(f[v]) 呢?因为在当前,他有多棵子树可以选,他当然选最大值最小的那棵(相当于更大的值因为不选而废了),所以就用 Σ 了(还是难理解?那我没办法了)
二号管理员控制时就反过来, f[i] 分别表示该一号选手选时当前比最终结果小的数最多有多少,当二号选手选时表示当前结果比最终结果少的数最多有多少,转移方程类似。
这种在不同时刻 f 的意义不同的,状态表示还这么巧妙的题真强。
题解·:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; const int N=200010, INF=1000000000; int n, mi, all; int head[N], f[N], g[N], chu[N]; struct Edge { int to,next; } e[N<<1]; inline void add(int u,int v) { e[++mi] = (Edge) { v,head[u] }; head[u] = mi; } void dfs1(int u,int fa,int dep) { for(int p=head[u]; p; p=e[p].next) if(e[p].to!=fa) dfs1(e[p].to, u, dep+1); if(!chu[u]) all++, f[u]=g[u]=1; else { if(dep&1) // 讨论这一步该谁选 { f[u] = INF; for(int p=head[u]; p; p=e[p].next) if(e[p].to!=fa) { f[u] = min(f[u], f[e[p].to]); // 一号管理员控制 g[u] += g[e[p].to]; // 二号管理员控制 } } else { g[u] = INF; for(int p=head[u]; p; p=e[p].next) if(e[p].to!=fa) { f[u] += f[e[p].to]; g[u] = min(g[u], g[e[p].to]); } } } } int main() { freopen("tree.in","r",stdin); freopen("tree.out","w",stdout); scanf("%d",&n); for(int i=1, u, v; i<n; ++i) { scanf("%d%d",&u,&v); add(u,v); add(v,u); chu[u]++; } dfs1(1,0,1); printf("%d %d\n",all-f[1]+1, g[1]); }
本蒟蒻第一次发题解,见谅!!!

