归并和快排
一、归并排序
核心思想:就是采用了经典的分治策略(分治法将问题分(divide)成一些小的问题,然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案“修补”在一起,即分而治之)
思路分析:对于"分"的阶段:我们只要找到数组的中间下标mid,然后将下标值小于等于mid的元素分成一个子数组,将下标值大于mid的元素也分成一个子数组;然后将分出来的两个子数组继续拆分,直到每个子数组只剩一个元素。 对于"治"的阶段:我们定义一个临时数组tmp,大小和拆分前的原始数组一样。用两个游标i和j,分别指向两个子数组的第一个元素。比较arr[i]和arr[j]大小,将小的元素先放到tmp数组,然后游标后移,直到其中一个数组元素全部遍历完,然后将另一个数组的剩余元素放到tmp的末尾。最后再把tmp数组的数据拷贝到原始数组。
图解:
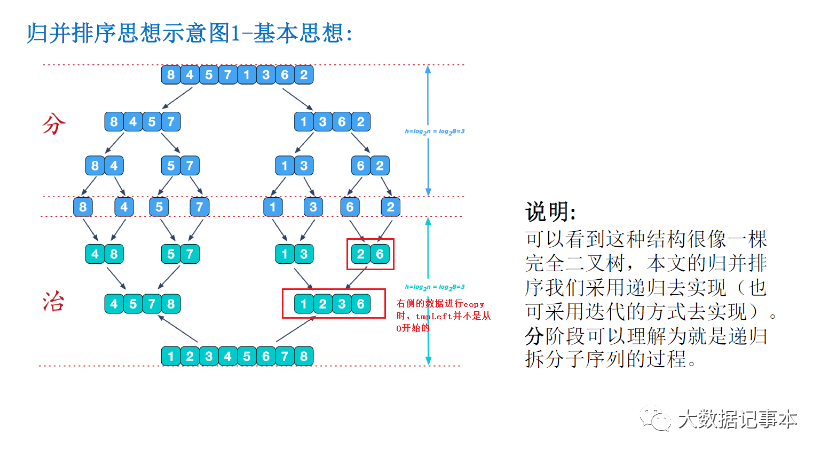
在"分"的阶段,我们把原始数组不断地从中间分开,形成两个新的数组,一直分到每个数组只剩一个元素
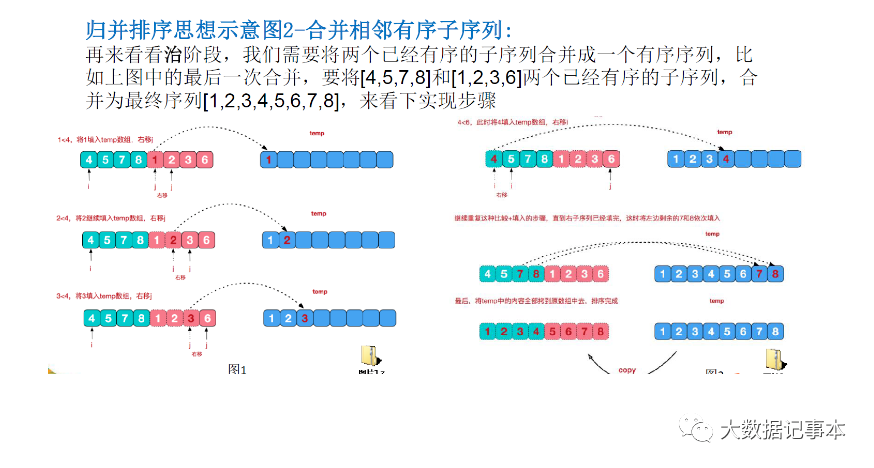
而在"治"的阶段,又把分成的多个数组两两按顺序合起来,从而形成最后排好序的数组。
下面用分析一下归并排序的好坏:
(1)归并排序是否是稳定排序算法
从上面的代码中我们可以看出,要判断归并排序是不是稳定关键要看merge()函数,在合并的过程中,由于arr[left,mid] 中元素的下标都小于 arr[mid+1,right] 的下标,我们的判断条件是:if (arr[i]<=arr[j]){tmp[t]=arr[i];t++;i++;},如果有相同的元素,下标小的合并时放入tmp数组的下标也小,在合并前后顺序是不变的,所以归并排序也是一种稳定的排序算法。
(2)归并排序的时间复杂度是多少
由于归并排序采用了递归,假设原始数组排序为问题a,两个子数组排序分别为问题b和问题c,对应的求解时间分别是 T(a), T(b) 和 T( c),那么就有:
T(a)=T(b)+T(c)+K
其中,K为子问题b和子问题c合并成问题a所花费的时间。
假设对 n 个元素进行归并排序需要的时间是 T(n),那分解成两个子数组排序的时间都是 T(n/2)。merge() 函数合并两个有序子数组的时间复杂度是 O(n)。所以,套用前面的公式,归并排序的时间复杂度的计算公式就是:
T(1) = C; n=1时,只需要常量级的执行时间,所以表示为C。T(n) = 2*T(n/2) + n;n>1
分解得:
T(n) = 2*T(n/2) + n = 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2*n = 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n = 8*(2*T(n/16) + n/8) + 3*n = 16*T(n/16) + 4*n ...... = 2^k * T(n/2^k) + k * n ......
得到 T(n) = 2^kT(n/2^k)+kn。当 T(n/2^k)=T(1) 时,也就是 n/2^k=1,我们得到 k=log2n 。将 k 值代入上面的公式,得到 T(n)=Cn+nlog2n 。如果我们用大 O 标记法来表示的话,T(n) 就等于 O(nlogn)。所以归并排序的时间复杂度是 O(nlogn)。
归并排序的执行效率与要排序的原始数组的有序程度无关,所以其时间复杂度是非常稳定的,不管是最好情况、最坏情况,还是平均情况,时间复杂度都是 O(nlogn)。
(3)归并排序的空间复杂度是多少
从上面分析可以看出,每次merge都需要一个和原始数组大小相同的tmp数组。所以归并排序并不是一个原地排序算法。
那么它的空间复杂度如何计算呢?尽管每次merge都需要申请一块和原始数组一样大的内存空间,但是合并完成之后,这个空间也就释放了。在任意时刻,只有一个函数在执行,也就只有一个临时数组在使用,所有临时空间最大也就是存放n个元素,所以空间复杂度是O(n)。
归并排序+求逆序对:(hdu4911)
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=100005; 4 typedef long long ll; 5 ll a[maxn], b[maxn], cnt;//cnt用于记录逆序对的数目 6 ll n, k; 7 void merge(ll l, ll mid, ll r){ 8 ll i=l, j=mid+1, t=0; 9 while(i<=mid && j<=r){ 10 if(a[i]>a[j]){ 11 b[t++]=a[j++]; 12 cnt+=mid-i+1; //记录逆序对的数量 13 } 14 else b[t++]=a[i++]; 15 } 16 //一个子序列中的数都处理完了,另一个还没有,把剩下的直接复制过去 17 while(i<=mid)b[t++]=a[i++]; 18 while(j<=r)b[t++]=a[j++]; 19 for(int i=0; i<t; i++)a[l+i]=b[i];//把排好序的b[]复制回a[] 20 } 21 void mergesort(ll l, ll r){ 22 if(l<r){ 23 ll mid=(l+r)/2; //平均分成两个子序列 24 mergesort(l, mid); // 25 mergesort(mid+1, r); // 26 merge(l, mid, r); //合并子序列 27 } 28 } 29 int main() 30 { 31 32 cin>>n; 33 for(int i=1; i<=n; i++)cin>>a[i]; 34 mergesort(1, n); 35 cout<<cnt; 36 return 0; 37 }
二、快速排序
快排利用的也是分治的思想。
- 如果要排序数组中begin到end之间的一组数据,我们选择begin到end之间的一个数据作为分区点(pivot)。
- 遍历begin到end之间的数据,将小于pivot的放到左边,大于pivot的放到右边。
- 经过这个步骤,数组begin到end之间就被分成了三个部分,begin到p-1之间的都是小于pivot的,中间是pivot,p+1到end之间的都是大于pivot的。
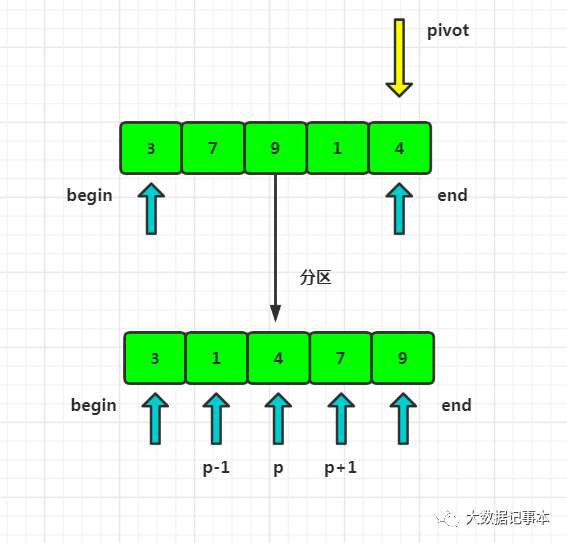
- 根据分治、递归的处理思想,我们可以用递归排序下标从 begin 到 p-1 之间的数据和下标从 p+1 到end 之间的数据,直到区间缩小为 1,就说明所有的数据都有序了。
思路分析:
这里定义一个 partition() 分区函数。partition() 分区函数就是随机选择一个元素作为 pivot(一般情况下,可以选择 begin 到end区间的最后一个元素),然后对 arr[begin…end]分区,函数返回 pivot 在数组中的下标。
为了让快排实现原地排序,即空间复杂度为O(1),这里的分区函数partition()必须是一个原地分区函数。它的实现思路如下:
- 定义一个游标i,将arr[begin,end-1]分成两部分,arr[begin...i-1]的元素都是小于pivot的,称为“已处理区域”,arr[i...end-1]是“未处理区域”。
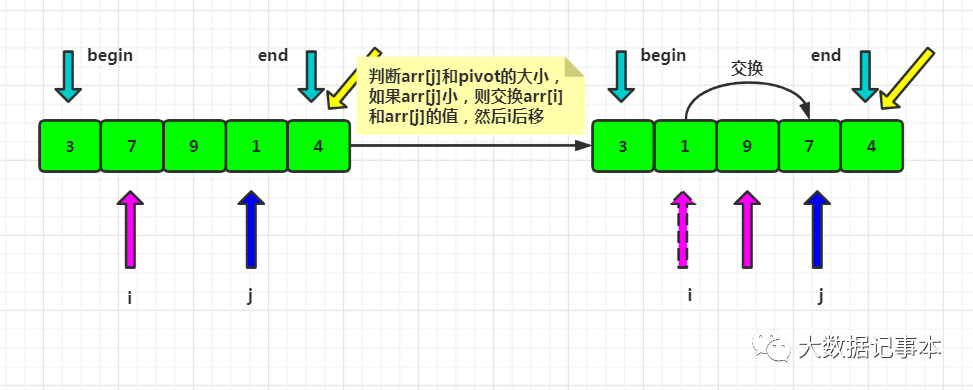
- 每次都从未处理区域arr[i...end-1]取一个元素arr[j],与pivot对比,如果小于等于pivot,则将其加入到已处理区间的尾部,即arr[i]的位置,然后i后移。
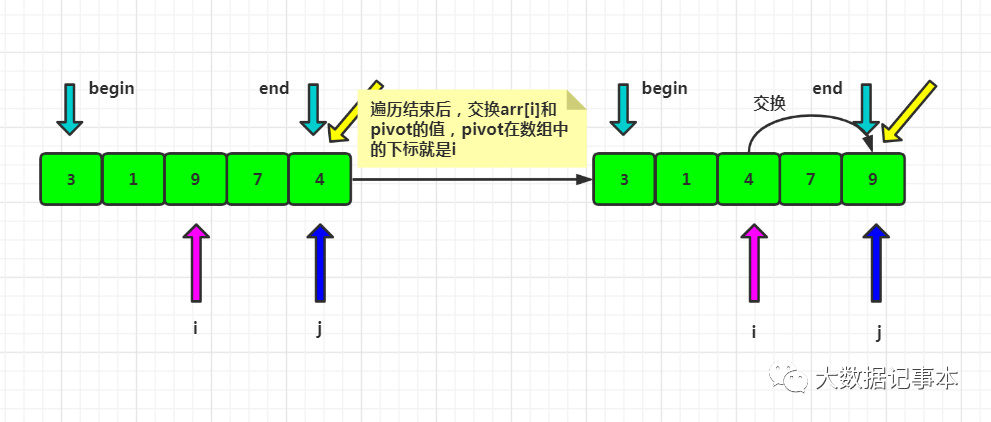
- 遍历结束后,i对应的位置就是排序后pivot的位置,所以交换arr[i]和pivot,此时pivot左边的数都小于等于pivot,右边的数都大于pivot。
图解:
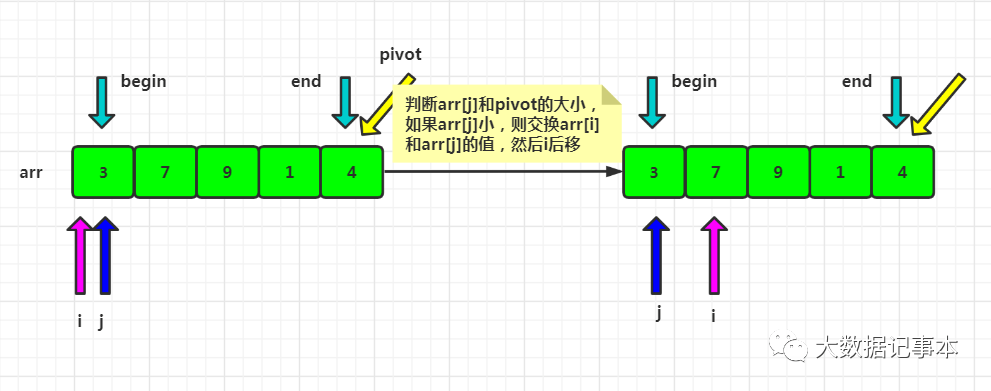
下面用分析一下快速排序的好坏:
(1)快速排序是否是稳定排序算法
因为分区的过程涉及交换操作,如果数组中有两个相同的元素,比如序列 5,7,5,3,4,在经过第一次分区操作时,3和第一个5会交换,两个5 的相对先后顺序就会改变。所以,快速排序并不是一个稳定的排序算法。
(2)快速排序是否是原地排序算法
上面分析中提到, 分区函数partition()是一个原地分区函数,所以快速排序是一个原地排序算法。
(3)快速排序的时间复杂度是多少
- 最好时间复杂度:快排也是用递归来实现的。对于递归代码的时间复杂度,上面归并排序的公式,这里也还是适用的。如果每次分区操作,都能正好把数组分成大小接近相等的两个小区间,那快排的时间复杂度递推求解公式跟归并是相同的。所以,快排的时间复杂度也是 O(nlogn)。
- 最坏时间复杂度:如果数组中的数据原来已经是有序的了,比如 1,2,3,4,5。如果每次选择最后一个元素作为 pivot,那每次分区得到的两个区间都是不均等的。我们需要进行大约 n 次分区操作,才能完成快排的整个过程。每次分区我们平均要扫描大约 n/2 个元素,这种情况下,快排的时间复杂度就从 O(nlogn) 退化成了 O(n^2)。
- 平均时间复杂度:O(nlogn)。
1.写法一:

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=1000010; 4 int n, a[maxn]; 5 void qsort(int l, int r){ 6 int i=l, j=r, mid=a[(i+j)/2]; 7 do{ 8 while(a[i]<mid)i++; 9 while(a[j]>mid)j--; 10 if(i<=j){ 11 swap(a[i], a[j]); 12 i++; j--; 13 } 14 }while(i<=j); 15 16 for(int k=1; k<=n; k++)cout<<a[k]<<" "; 17 cout<<endl; 18 19 if(l<j)qsort(l, j); 20 if(i<r)qsort(i, r); 21 } 22 int main() 23 { 24 cin>>n; 25 for(int i=1; i<=n; i++)cin>>a[i]; 26 qsort(1, n); 27 for(int i=1; i<=n; i++)cout<<a[i]<<" "; cout<<endl; 28 29 return 0; 30 }
2.写法二:(POJ2338)
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=10010; 4 int data[maxn]; 5 int partition(int left, int right){ //划分成左、右两部分,以i指向的数为边界 6 int i=left; 7 int temp=data[right]; //把尾部的数看成基准数 8 for(int j=left; j<right; j++){ 9 if(data[j] < temp){ 10 swap(data[j], data[i]); 11 i++; 12 } 13 } 14 swap(data[i], data[right]); 15 return i; //返回基准数的位置 16 } 17 void quicksort(int left, int right){ 18 if(left<right){ 19 int i=partition(left, right); //划分 20 quicksort(left,i-1); //分治:i左边的继续递归划分 21 quicksort(i+1,right); //分治:i右边的继续递归划分 22 } 23 } 24 int main() 25 { 26 int n; 27 cin>>n; 28 for(int i=1; i<=n; i++)cin>>data[i]; 29 quicksort(1, n); 30 for(int i=1; i<=n; i++)cout<<data[i]<<" "; cout<<endl; 31 cout<<data[(1+n)/2]; 32 return 0; 33 }
3.求前第k大的数(hud1425)(时间复杂度为O(n)) 为什么基于快排的查找第k大数时间复杂度是O(n)?
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=10010; 4 int data[maxn]; 5 int n, k; 6 int partition(int left, int right){ 7 int i=left; 8 int temp=data[right]; 9 for(int j=left; j<right; j++){ 10 if(data[j] < temp){ 11 swap(data[j], data[i]); 12 i++; 13 } 14 } 15 swap(data[i], data[right]); 16 return i; 17 } 18 int quicksort(int left, int right){ 19 if(left<right){ 20 int i=partition(left, right); 21 if(i>k)return quicksort(left,i-1); 22 else if(i<k)return quicksort(i+1,right); 23 else return data[i]; 24 } 25 } 26 int main() 27 { 28 29 cin>>n>>k; 30 for(int i=1; i<=n; i++)cin>>data[i]; 31 32 cout<<quicksort(1,n); 33 return 0; 34 }
总结:
| 原地排序 | 稳定 | 最好时间复杂度 | 最差时间复杂度 | 平均时间复杂度 | |
| 快速排序 | 是 | 否 | O(nlogn) | O(n^2) | O(nlogn) |
| 归并排序 | 否 | 是 | O(nlogn) | O(nlogn) | O(nlogn) |




 浙公网安备 33010602011771号
浙公网安备 33010602011771号