蓝桥杯算法集训 - Week 2：双指针、归并排序、多路归并

蓝桥杯算法集训 - Week 2

本系列随笔用于整理AcWing题单——《蓝桥杯集训·每日一题2024》的系列题型及其对应的算法模板。

一、双指针

Ⅰ、代码模板

常见问题分类：
(1) 对于一个序列，用两个指针维护一段区间
(2) 对于两个序列，维护某种次序，比如归并排序中合并两个有序序列的操作

for (int i = 0, j = 0; i < n; i++) {
    while (j < i && check(i, j)) j++;

    // 解决问题的具体逻辑
    // ...
}

Ⅱ、无重复字符的最长子串

3. 无重复字符的最长子串 - 力扣

class Solution {
    public int lengthOfLongestSubstring(String s) {
        // 哈希集合，记录每个字符是否出现过
        Set<Character> occ = new HashSet<Character>();
        int n = s.length();
        // 右指针，初始值为 -1，相当于我们在字符串的左边界的左侧，还没有开始移动
        int ans = 0;
        for (int i = 0, rk = -1; i < n; ++i) {
            if (i != 0) {
                // 左指针向右移动一格，移除一个字符
                occ.remove(s.charAt(i - 1));
            }
            while (rk + 1 < n && !occ.contains(s.charAt(rk + 1))) {
                // 不断地移动右指针
                occ.add(s.charAt(rk + 1));
                ++rk;
            }
            // 第 i 到 rk 个字符是一个极长的无重复字符子串
            ans = Math.max(ans, rk - i + 1);
        }
        return ans;
    }
}

二、归并排序

归并排序原理复习参考：归并排序 - Hello 算法

Ⅰ、代码模板

static void mergeSort(int q[], int l, int r) {
    if (l >= r) return;

    int mid = l + (r - l) / 2;
    mergeSort(q, l, mid);
    mergeSort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k++] = q[i++];
        else tmp[k ++ ] = q[j ++ ];

    while (i <= mid) tmp[k++] = q[i++];
    while (j <= r) tmp[k++] = q[j++];

    for (i = l, j = 0; i <= r; i ++, j ++) q[i] = tmp[j];
}

Ⅱ、超快速排序

107. 超快速排序 - AcWing题库

import java.io.*;

public class Main {
	static final int N = 500010;
	static int n;
	static long res;
	static int[] a = new int[N], temp = new int[N];

	public static void main(String[] args) throws NumberFormatException, IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		n = Integer.parseInt(br.readLine());
		while (n != 0) {
			res = 0;
			for (int i = 0; i < n; i++)
				a[i] = Integer.parseInt(br.readLine());
			mergeSort(a, 0, n - 1);
			System.out.println(res);
			
			n = Integer.parseInt(br.readLine());
		}
		br.close();
	}

	// 归并排序模板
	static void mergeSort(int q[], int l, int r) {
		if (l >= r)
			return;

		int mid = l + (r - l) / 2;
		mergeSort(q, l, mid);
		mergeSort(q, mid + 1, r);

		int k = 0, i = l, j = mid + 1;
		while (i <= mid && j <= r) {
			if (q[i] <= q[j])
				temp[k++] = q[i++];
			else { // 顺序需要调整
				res += mid - i + 1; // 记录逆序对
				temp[k++] = q[j++];
			}
		}

		while (i <= mid)
			temp[k++] = q[i++];
		while (j <= r)
			temp[k++] = q[j++];

		for (i = l, j = 0; i <= r; i++, j++)
			q[i] = temp[j];
	}
}

三、多路归并

多路归并复习参考：多路归并排序的原理和Java实现

Ⅰ、代码模板

// 多路归并模板——基于优先队列
static List<Integer> kMergeSort(int[][] data) {
	if (data == null || data.length == 0) {
		return null;
	}
	List<Integer> result = new ArrayList<>();

	// 建立一个优先队列，指定比较器为升序
	PriorityQueue<int[]> queue = new PriorityQueue<>((a, b) -> a[0] - b[0]);
	// 将每个子序列的第一个元素加入优先队列中
	for (int i = 0; i < data.length; i++) {
		if (data[i].length > 0) {
			// 每个元素是一个数组，包含三个信息：值，所在行号，所在列号
			queue.offer(new int[]{data[i][0], i, 0});
		}
	}
	// 当优先队列不为空时循环执行
	while (!queue.isEmpty()) {
		// 弹出队列顶元素，并将其值添加到结果集合中
		int[] min = queue.poll();
		result.add(min[0]);
		// 如果该元素所在子序列还有下一个元素，则将其加入优先队列中
		if (min[2] + 1 < data[min[1]].length) {
			queue.offer(new int[]{data[min[1]][min[2] + 1], min[1], min[2] + 1});
		}
	}
	// 返回结果集合
	return result;
}

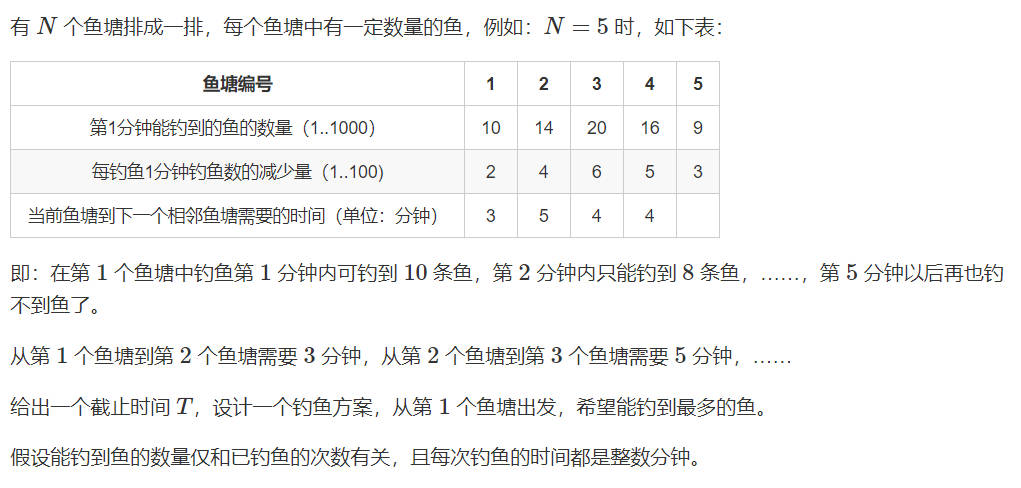
Ⅱ、鱼塘钓鱼

1262. 鱼塘钓鱼 - AcWing题库

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.PriorityQueue;

public class Main {
	static final int N = 110;
	static int n, t;
	static int[] c = new int[N], d = new int[N], prefix = new int[N];

	public static void main(String[] args) throws NumberFormatException, IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		n = Integer.parseInt(br.readLine());
		String[] split = br.readLine().split(" ");
		for (int i = 0; i < n; i++) {
			c[i] = Integer.parseInt(split[i]);
		}
		split = br.readLine().split(" ");
		for (int i = 0; i < n; i++) {
			d[i] = Integer.parseInt(split[i]);
		}
		split = br.readLine().split(" ");
		for (int i = 1; i <= n - 1; i++) {
			prefix[i] = prefix[i - 1] + Integer.parseInt(split[i - 1]);
		}
		t = Integer.parseInt(br.readLine());
		br.close();
		
		int res = 0;
		for (int i = 1; i <= n; i++) {
			// 枚举经过鱼塘数从 1 到 n 的最大鱼数
			res = Math.max(res, kMerge(Arrays.copyOfRange(c, 0, i)).stream().reduce(Integer::sum).orElse(0));
		}
		System.out.println(res);
	}

	// 多路归并获取最大 res 集合
	static List<Integer> kMerge(int[] a) {
		if (a == null || a.length == 0) {
			return null;
		}

		List<Integer> res = new ArrayList<Integer>();
		PriorityQueue<int[]> queue = new PriorityQueue<>((arr1, arr2) -> Integer.compare(arr2[0], arr1[0]));
		for (int i = 0; i < a.length; i++) {
			queue.offer(new int[] { a[i], i });
		}

		int time = t - prefix[a.length - 1]; // 贪心：最优路线总是从前往后而不折返，即减去当前子结构的消耗时间（前缀和）
		while (time > 0 && !queue.isEmpty()) {
			int[] max = queue.poll();
			res.add(max[0]);
			a[max[1]] -= d[max[1]]; // 衰减鱼塘的鱼量
			
			if (a[max[1]] > 0) {
				queue.offer(new int[] { a[max[1]], max[1] }); // 将收益不为零的鱼塘加入队列
			}

			time--;
		}

		return res;
	}
}