poj3764-The xor-longest Path

Description

In an edge-weighted tree, the xor-length of a path p is defined as the xor sum of the weights of edges on p:

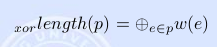⊕ is the xor operator.

We say a path the xor-longest path if it has the largest xor-length. Given an edge-weighted tree with n nodes, can you find the xor-longest path? 　

Input

The input contains several test cases. The first line of each test case contains an integer n(1<=n<=100000), The following n-1 lines each contains three integers u(0 <= u < n),v(0 <= v < n),w(0 <= w < 2^31), which means there is an edge between node u and v of length w.

Output

For each test case output the xor-length of the xor-longest path.

Sample Input

4
0 1 3
1 2 4
1 3 6

Sample Output

7

Hint

The xor-longest path is 0->1->2, which has length 7 (=3 ⊕ 4)

题意:求树上两点路径的异或和的最大值

用d[x]表示根到x路径上所有边权的异或和，由异或的性质，x到y路径上所有边权的异或和等于d[x] xor d[y]，所以就是在d[0]-d[n-1]中找两个数，使得异或之后最大。
把每个整数看作长度为31的01串（数值较小的在前面补0），然后插入到一棵字典树中
每次查找一个数，先尝试沿着与当前位相反的字符指针向下访问，如果没有就访问相同的，这样构造出来的一定是与当前查找的数做xor运算结果最大的。

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
//#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N=2e5+100;
int n,cnt,tot;
int last[N],d[N];
struct tree{
    int v,nex,w;}t[N*2];
int trie[N*32][2];
void add(int x,int y,int z)
{
    cnt++;
    t[cnt].v=y;
    t[cnt].nex=last[x];
    last[x]=cnt;
    t[cnt].w=z;
}
void dfs(int x,int fa,int dis)
{
    d[x]=dis;
    for (int i=last[x];i;i=t[i].nex)
    {
        if (t[i].v==fa) continue;
        dfs(t[i].v,x,dis^t[i].w);
    }
}

void Insert(int x)
{
    int p=0,now;
    for (int i=31;i>=0;i--)
    {
        now=(x>>i)&1;
        if (!trie[p][now]) trie[p][now]=++tot;
        p=trie[p][now];
    }
}
int fund(int x)
{
    int p=0,now,ret=0;
    for (int i=31;i>=0;i--)
    {
        now=!((x>>i)&1);
        ret<<=1;
        if (trie[p][now])
        {
            p=trie[p][now];
            ret++;
        }
        else p=trie[p][!now];
    }
    return ret;
}
int main()
{
    while(scanf("%d",&n)!=EOF)
    {
        memset(last,0,sizeof(last));
        memset(trie,0,sizeof(trie));
        cnt=0; tot=0;

        int x,y,z;
        for (int i=1;i<n;i++)
        {
            scanf("%d%d%d",&x,&y,&z);
            add(x,y,z); add(y,x,z);
        }
        d[0]=0;
        dfs(0,-1,0);

        int ans=0;
        for (int i=0;i<n;i++) Insert(d[i]);
        for (int i=0;i<n;i++) ans=max(ans,fund(d[i]));
        printf("%d\n",ans);
    }

    return 0;
}