树状数组

什么是树状数组

树状数组其实是一个数组，只是每个节点维护的信息是某一段区间的信息。

树状数组原理

对于长度为8的数组\(A[8]\)，如果我们对其建立线段树，如下图所示：

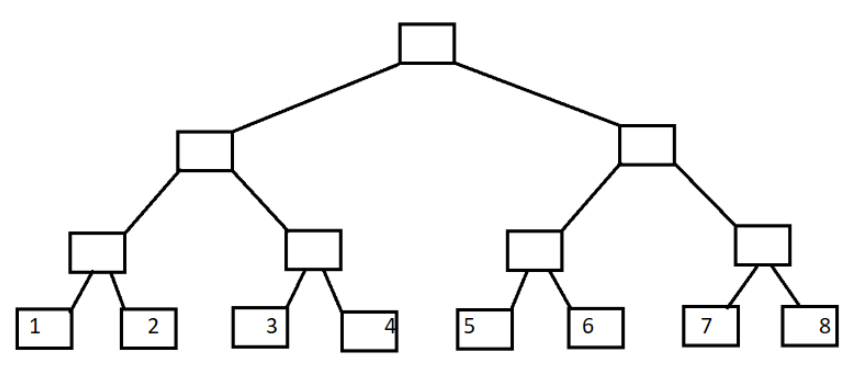
线段树中每个节点维护的也是一段区间的信息，对于节点\(x\)，维护的区间为\([l,r]\)，那么他的左儿子\(x*2\)，维护的区间就是\([l,mid]\)，右儿子\(x*2+1\)维护的区间就是\([mid+1,r]\)。

那么如果我们建立树状数组，情况会是这个样子：

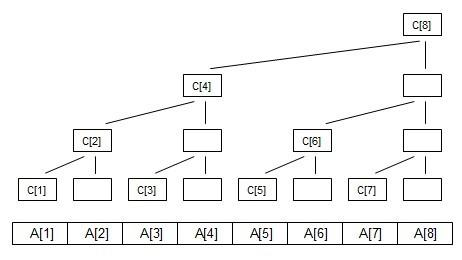
\(C[i]\)为树状数组的节点，更直白一点展示每个节点维护的区间的信息，如下图所示：

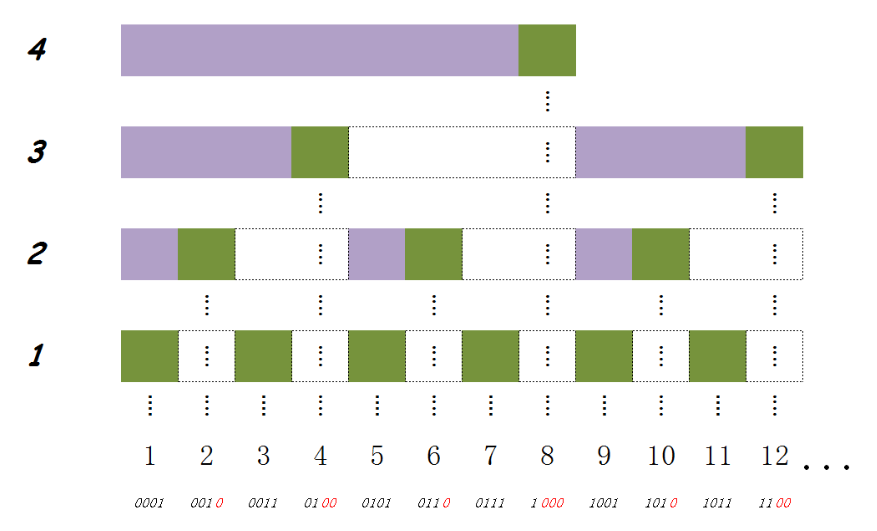
树状数组是二进制思想的经典应用。与线段树不同，树状数组中每一个元素的编号变成了二进制编码，如\(6=(110)_2\)，再通过这些二进制编码末尾0的个数来决定存储什么信息，假设节点编号为\(x\)，那么这个节点存储数据的区间为\(2^k\)（\(k\)为\(x\)二进制末尾0的个数）个元素，即这个节点存储的数据为\(A[x-2^n+1]+…+A[x]\)。

在这里我们引入\(lowbit(x)\)来替代上文的\(2^k\)，\(lowbit(x)\)表示\(x\)的二进制表示中最低的一位1所对应的值，即\(lowbit(6)=(10)_2=2\)。

到现在，我们可以得到树状数组的一些性质：
①每个节点维护的区间的长度是2的幂；
②上一层节点维护的区间的长度是下一层的两倍；
③一个节点只要补上自己维护的区间的长度就可以得到下一个包含这段区间的节点。

lowbit(x)的实现

int lowbit(x) {   
    return x & -x;
}

这个式子运用了计算机的补码计算原理，补码是原码的反码反加一。如：\((0110)_2=6\)，变为反码后为\(0001\)，再加一为\(0010\)即它的补码。可以发现变为反码后\(x\)与反码数字位每一位都不同， 所以当反码加1后，逢1一直进位直到遇到0，且这个0变成了1，所以这个数最后面出现了一个100…串。由于是反码，进位之后由于1的作用使进位的部分全部取反及与原码相同，所以可以发现\(lowbit\)以前的部分\(x\)和\(-x\)补码相反，\(lowbit\)位\(x\)和\(-x\)都是1，\(lowbit\) 以后\(x\)和\(x\)都是0 所以\(x\&-x\)后除了\(lowbit\)位是1，其余位都是0。

求和操作

假如现在我们如果想求\(Sum(6)\)，首先要加上\(C[6]\)，如上文所述\(C[6]\)表示的是右端点为6，长度为\(lowbit(6)=2\)的区间和，因此下面我们要再加上\(C[6-lowbit(6)]\)即\(C[4]\)，而\(C[4]\)表示的是右端点为4，长度为\(lowbit(4)=4\)的区间和，计算完成。可以看出，这是一个二进制下的加法运算\(110=100+10\)，把长度为6的区间拆分成长度为4和2的区间。结合上图，便很好理解了。

int Sum(int x) {
	int sum=0;
	while(x) {
		sum += C[x];
		x -= lowbit(x);
	}
	return sum;
}

修改操作

和求和操作类似，如果我们现在修改了一个点的值，那么我们就要去修改在树状数组维护的区间内有这个点的点。根据上面所提到的性质③，我们只需要让不断地让\(x+lowbit(x)\)即可。

void update(int x,int val) {
	while(x <= n) {
		C[x] += val;
		x += lowbit(x);
	}
}

参考：
2009年国家集训队论文 浅谈信息学竞赛中的“0”和“1”——武森
https://blog.csdn.net/flushhip/article/details/79165701