杭电多校第一场-M-Code
题目描述
After returning with honour from ICPC(International Cat Programming Contest) World Finals, Tom decides to say goodbye to ICPC and start a new period of life. He quickly gets interested in AI.
In the subject of Machine Learning, there is a classical classification model called perceptron, defined as follows:
Assuming we get a set of training samples: D={(x1,y1),(x2,y2),...,(xN,yN)}, with their inputs x∈Rd, and outputs y∈{−1,1}. We will try to find a function
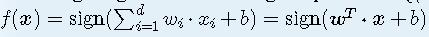 so that f(xi)=yi,i=1,2,...,N.
so that f(xi)=yi,i=1,2,...,N.
w,x mentioned above are all d-dimensional vectors, i.e. w=(w1,w2,...,wd), x=(x1,x2,...,xd). To simplify the question, let w0=b, x0=1, then
In the subject of Machine Learning, there is a classical classification model called perceptron, defined as follows:
Assuming we get a set of training samples: D={(x1,y1),(x2,y2),...,(xN,yN)}, with their inputs x∈Rd, and outputs y∈{−1,1}. We will try to find a function
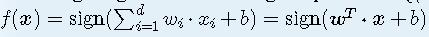 so that f(xi)=yi,i=1,2,...,N.
so that f(xi)=yi,i=1,2,...,N.w,x mentioned above are all d-dimensional vectors, i.e. w=(w1,w2,...,wd), x=(x1,x2,...,xd). To simplify the question, let w0=b, x0=1, then

Therefore, finding a satisfying function f(x) is equivalent to finding a proper w.
To solve the problem, we have a algorithm, PLA(Popcorn Label Algorithm).
Accoding to PLA, we will randomly generate w.
If f(x)=sign(wT⋅x) fails to give
any element (xi,yi)∈D the right classification, i.e. f(xi)≠yi, then we will replace w with another random vector. We will do this repeatedly until all the samples ∈D are correctly classified.
As a former-JBer, Tom excels in programming and quickly wrote the pseudocode of PLA.
w := a random vector
while true do
flag:=true
for i:=1 to N do
if f(x[ i ]) != y[ i ] then
flag:=false
break
if flag then
break
else
w := a random vector
return w
But Tom found that, in some occasions, PLA will end up into an infinite loop, which confuses him a lot. You are required to help Tom determine, when performed on a given sample set D, if PLA will end up into an infinite loop. Print Infinite loop! if so, or Successful! otherwise.
We only consider cases when d=2 for simplification.

To solve the problem, we have a algorithm, PLA(Popcorn Label Algorithm).
Accoding to PLA, we will randomly generate w.
If f(x)=sign(wT⋅x) fails to give
any element (xi,yi)∈D the right classification, i.e. f(xi)≠yi, then we will replace w with another random vector. We will do this repeatedly until all the samples ∈D are correctly classified.
As a former-JBer, Tom excels in programming and quickly wrote the pseudocode of PLA.
w := a random vector
while true do
flag:=true
for i:=1 to N do
if f(x[ i ]) != y[ i ] then
flag:=false
break
if flag then
break
else
w := a random vector
return w
But Tom found that, in some occasions, PLA will end up into an infinite loop, which confuses him a lot. You are required to help Tom determine, when performed on a given sample set D, if PLA will end up into an infinite loop. Print Infinite loop! if so, or Successful! otherwise.
We only consider cases when d=2 for simplification.

输入
The first line contains an integer T(1≤T≤1000), the number of test cases.
Each test case begins with a line containing a single integer n(1≤n≤100), size of the set of training samples D.
Then n lines follow, the ith of which contains three integers xi,1,xi,2,yi (−105≤xi,1,xi,2≤105, yi∈{−1,1}), indicating the ith sample (xi,yi) in D, where xi=(xi,1,xi,2).
Each test case begins with a line containing a single integer n(1≤n≤100), size of the set of training samples D.
Then n lines follow, the ith of which contains three integers xi,1,xi,2,yi (−105≤xi,1,xi,2≤105, yi∈{−1,1}), indicating the ith sample (xi,yi) in D, where xi=(xi,1,xi,2).
输出
For each test case, output a single line containing the answer: “Infinite loop!” or “Successful!”.
题意是给你n个三元组(x1,x2,y),问你是否存在a,b,c使得对所有的三元组满足sgn(ax1+bx2+c)=y; 官方题解: d=2 时,f(x) =sgn(ax1+bx2+c),f(x) = 0 对应于二维平面上的一条直线,直线一侧的点取值为 1,直线另一侧的取值为 -1。 故该问题等价于能否找到一条直线将平面上的两类点分开,等价于判断这两类点分别组成的两个凸包是否相交。
判断凸包是否相交,参考https://www.cnblogs.com/ITUPC/p/5987593.html

#include <bits/stdc++.h> #define ll long long using namespace std; const double eps=1e-8; const int N=150; int sgn(double x) { if (fabs(x)<eps)return 0; if (x<0)return -1; else return 1; } struct Point { ll x,y; Point() {} Point(ll _x,ll _y) { x=_x; y=_y; } Point operator -(const Point &b) { return Point(x-b.x,y-b.y); } ll operator ^(const Point &b) { return x*b.y-y*b.x; } ll operator *(const Point &b) { return x*b.x+y*b.y; } bool operator<(const Point &b)const { if(fabs(y-b.y)<eps) return x<b.x; return y<b.y; } }; double Length(Point A) { return sqrt(A*A); } double Angle(Point A,Point B) { return acos((A*B)/Length(A)/Length(B)); } bool Inter(Point a1,Point a2,Point b1,Point b2) { ll c1=(a2-a1)^(b1-a1),c2=(a2-a1)^(b2-a1),c3=(b2-b1)^(a1-b1),c4=(b2-b1)^(a2-b1); return sgn(c1)*sgn(c2)<0&&sgn(c3)*sgn(c4)<0; } int Graham(Point p[],int n,Point q[]) { int top=1; sort(p,p+n); if (n==0) return 0; q[0]=p[0]; if (n==1) return 1; q[1]=p[1]; if (n==2) return 2; q[2]=p[2]; for (int i=2;i<n;i++) { while(top&&((q[top]-q[top-1])^(p[i]-q[top-1]))<=0) top--; q[++top]=p[i]; } int len=top; q[++top]=p[n-2]; for (int i=n-3;i>=0;i--) { while (top!=len&&((q[top]-q[top-1])^(p[i]-q[top-1]))<=0) top--; q[++top]=p[i]; } return top; } bool C_S(Point ch1[],int t1,Point ch2[],int t2) { if (t1==1) return 1; double angle[1050],x; int i,j,k; if (t1==2) { for(i=0;i<t2;i++) { k=sgn((ch1[1]-ch1[0])^(ch2[i]-ch1[0])); if (k==0 && (ch1[1]-ch1[0])*(ch2[i]-ch1[0])>0) { if (Length(ch2[i]-ch1[0])<Length(ch1[1]-ch1[0])) break; } } if (i<t2) return 0; if (t2==2 && Inter(ch1[0],ch1[1],ch2[0],ch2[1])) return 0; return 1; } angle[0]=0; for (int i=2;i<t1;i++) angle[i-1]=Angle(ch1[1]-ch1[0],ch1[i]-ch1[0]); for (i=0;i<t2;i++) { j=sgn((ch1[1]-ch1[0])^(ch2[i]-ch1[0])); if (j<0 || (j==0 && (ch1[1]-ch1[0])*(ch2[i]-ch1[0])<0)) continue; j=sgn((ch1[t1-1]-ch1[0])^(ch2[i]-ch1[0])); if (j>0 || (j==0 && (ch1[t1-1]-ch1[0])*(ch2[i]-ch1[0])<0)) continue; x=Angle(ch1[1]-ch1[0],ch2[i]-ch1[0]); int m=lower_bound(angle,angle+t1-1,x)-angle; if (m==0) j=0; else j=m-1; k=sgn((ch1[j+1]-ch2[i])^(ch1[j+2]-ch2[i])); if (k>=0) break; } if (i<t2) return 0; return 1; } Point p1[N],p2[N],ch1[N],ch2[N]; int T,n; int main() { //freopen("1.in","r",stdin); //freopen("1.out","w",stdout); scanf("%d",&T); while(T--) { scanf("%d",&n); int cnt1=0,cnt2=0; ll x,y; int z; for(int i=0;i<n;i++) { scanf("%lld%lld%d",&x,&y,&z); if (z==1) p1[cnt1++]=Point(x,y); else p2[cnt2++]=Point(x,y); } int t1=Graham(p1,cnt1,ch1); int t2=Graham(p2,cnt2,ch2); if (C_S(ch1,t1,ch2,t2)&&C_S(ch2,t2,ch1,t1)) printf("Successful!\n"); else printf("Infinite loop!\n"); } //fclose(stdin); //fclose(stdout); return 0; }




【推荐】还在用 ECharts 开发大屏?试试这款永久免费的开源 BI 工具!
【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步