计算几何 poj 3347
题意:依次给出n个正方形的边长,要求在第一象限内依次放入正方形,满足:
①放入第i个正方形时,第i个正方形与前面的正方形都不重合
②放入正方形时,要求一个顶点在x轴上,且坐标值最小
其实看这个图就懂规则了
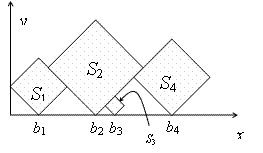
求放完所有正方形后,从高处向下照射竖直平行光,有部分会被照亮的正方形序号。
题解:
该题事实上只用到投影长度,将数据放大根号2倍,显然结果不变,但就只涉及整数计算,避免了精度问题
设正方形边长为s[i]=读入数据*根号2,顶点坐标为t[i]
考虑两件事——如何放正方形和如何判断是否被照亮:
放置①放第i个正方形的时候,扫描前i-1个正方形,now=max{s[k]+2*min{s[k],s[i]}},t[i]=max{now,s[i]}
判断②对第i个正方形,扫描1~i-1个正方形,l=max{s[j]+s[i]-(t[i]-t[j])},扫描i+1~n个正方形,r=max(r,s[j]+s[i]-(t[j]-t[i])),如果l+r<2*s[i],这个正方形就有被照亮的地方
写这种水题的时候常会失智,莫名写上半天
#include<cmath> #include<cstdio> #include<cstring> #include<algorithm> using namespace std; #define rep(i,a,b) for(int i=a;i<=b;++i) int n,k,now,r,l; int s[100],t[100]; int main() { while (~scanf("%d",&n)) { if (n==0) break; rep(i,1,n) scanf("%d",s+i); t[1]=s[1]; rep(i,2,n) { now=0; rep(j,1,i-1) now=max(now,t[j]+2*min(s[i],s[j])); now=max(now,s[i]); t[i]=now; } rep(i,1,n) { l=0;r=0; rep(j,1,i-1) if (s[j]>s[i]) l=max(l,s[j]+s[i]-(t[i]-t[j])); rep(j,i+1,n) if (s[j]>s[i]) r=max(r,s[j]+s[i]-(t[j]-t[i])); if (l+r<2*s[i]) printf("%d ",i); } printf("\n"); } }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号