Redis Hyperloglog的原理及数学理论的通俗理解

redis中有一种数据格式，hyperloglog，本文就此数据结构的作用、redis的实现及其背后的数学原理作一个整理。当然本文不包含任何数学公式，而是希望用直观的例子帮大家理解。
主要内容如下：
1.业务场景
2.使用效果
3.数学原理
4.redis的实现原理

1.业务场景

现在有这样一个业务场景，统计某个页面的uv。和pv不同，在统计uv的时候需要根据用户id进行去重，因此就很难用一个简单的累加计数器来累加pv。当用户量达到千万甚至更高级别的时候，去重所需要的额外存储空间将是巨大的。而hyperloglog数据结构正是用来解决这类问题的，它用仅仅12kb的字节，就能统计\(2^{64}\)数量级别的去重数据统计。当然这种统计是一种估计量，当数量足够大的时候，误差在1%左右。因此如果我们要求的统计结果不需要特别精确，那么就可以使用这种数据结构节省大量存储空间。

2.使用效果

我们先看下使用效果，分别记录1000、10000、100000个不同的id，观察统计数据 ：

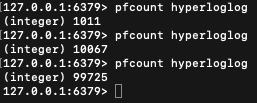
可以看到每次的统计结果都略有误差，但在可接受范围内。

3.数学原理

极大似然估计的直观理解

其使用的数学原理是统计学中的极大似然估计。接下去我将用多个场景逐步深入解析。
场景1：现在有2个不透明的口袋，其中都装有100个球，A口袋中是99个白球1个黑球，B口袋中是99个黑球1个白球。当我们随机挑选一个口袋，然后从中拿出一个球。如果拿出的球是白色的，那么我们可以说“大概率”我们取出的是A口袋。这种直觉的推测其实就包含了“极大似然估计”的思想。

场景2：我们只保留A口袋，其中99个白球，1个黑球。很容易我们就可以得出结论，从中取出任意一个球，是白球的概率为99%，是黑球的概率为1%。这是一种正向的推测：
我们知道了条件（99个白球，1个黑球），从而推测出结果（取出任意一个球，是白球的概率为99%）。
但这只是理论上的推测，如果实际取球100次，每次都放回，那么取出黑球的次数并不一定是1次，可能是0次，也可能超过1次。我们取球的次数越多，实际情况将越符合理论情况。

场景3：还是A口袋，只不过此时其中白球和黑球的数量我们并不知晓。于是我们开始从中拿球，每拿出一个球都记录下结果，并将其放回。如果我们取球100次，其中99次是白球，1次是黑球，我们可以说A口袋中可能是99个白球，但并不能非常肯定。当我们取球10000次的时候，其中9900次是白球，100次是黑球，此时我们就可以大概率确定A口袋中是99个白球，而这种确定程度随着我们实际取球次数的增加也将不断增加。这就是一种反向的推测：
我们观察了结果（取10000次球，9900次是白球，100次是黑球），可以推测出条件（A口袋中放了99个白球，1个黑球）。
当然这种推测的结果并非是准确的，而是一种大概率的估计。
无论是正向推测或是反向推测，只有当实际执行操作的次数足够多的时候，才能使得实际情况更接近理论推测。这就非常符合hyperloglog的特点，只有当数据量足够大的时候，误差才会足够小。

因此极大似然估计的本质就是：当能观察的结果数量足够多时，我们就可以大概率确定产生相应结果所需要的条件的状态。这种通过大量结果反向估计条件的数学方法就是极大似然估计。

伯努利实验与极大似然估计

了解极大似然估计之后，我们就需要引入第二个数学概念，伯努利实验。
不要被这个名字唬住，伯努利实验其实就是扔硬币，接下去我们就来了解下这枚硬币要怎么扔。下文所说的硬币都是最普通的硬币，只有正反两面，且每一面朝上的概率都是50%。
场景1：我们随机扔一次硬币，那么得到正面或反面的可能性是相同的。如果我们扔10000次硬币，那么可以估计到大概率是接近5000次正面，5000次反面。这是最简单的正向推测。

场景2：如果我们扔2次硬币，是否可能2次都是正面？当然有可能，并且概率为1/4。如果我们扔10次硬币呢，是否可能10次都是正面？虽然概率很小，但依然是有可能的，概率为1/1024。同样的，无论是100次、1000次，即使概率很小，也依然存在全部都是正面朝上的情况，假如扔了n次，那么n次都是正面的概率为\(\frac{1}{2^n}\)。这也是正向的推测，只不过增加了全都是正面朝上的限定。

场景3：现在我们按下面这种规则扔硬币：不断扔硬币，如果是正面朝上，那么就继续扔，直到出现反面朝上，此时记录下扔硬币的总次数。例如我们抛了5次硬币，前4次都是正面朝上，第5次是反面朝上，我们就记录下次数5。通过场景2，我们可以知道这种情况发生的概率为1/32。按我们的直觉可以推测，如果一个结果发生的概率是1/32，那么我们大体上就需要做32次同样的事情才能得到这个结果（当然从更严谨的数学角度，并不能这么说，但本文不想涉及专业的数学描述，所以姑且这么理解，其实也挺符合一般常识判断的）。
那么假如张三做了若干次这种实验，我观察结果，发现记录下的总次数的最大值是5，那就说明在这若干次实验中，至少发生了一次4次正面朝上，第5次反面朝上的情况，而这种情况发生的概率是1/32，于是我推测，张三大概率总共做了32次实验。这就是一种反向推测：
即根据结果（发生了一次1/32概率才会出现的结果），推测条件（大概率做了32次实验）。
更通俗来说，如果一个结果出现的概率很小，但却实际发生了了，就可以推测这件事情被重复执行了很多次。结果出现的概率越小，事情被重复执行的次数就应当越多。就像生活中中彩票的概率很低，普通人如果想中那可不就得买很多次嘛，中奖概率越低，一般需要购买彩票的次数就越多。相应的如果一个人中奖了，我们可以说这个人大概率上购买了非常多次彩票。这就是伯努利实验与极大似然估计结合的通俗理解。

另外特别注意的，我们推测条件时，需要观察的总次数的最大值，因为最大值代表了最小概率，而最小概率才是推测条件的依据。下文redis同理。

Redis中的实现

在redis中扔硬币

redis实现本质也是利用了“扔硬币”产生的“极大似然估计”原理，因此接下去我们就详细看看redis是怎么扔硬币的。
在伯努利试验的场景3中，我们做的实验有3个特点：
1.硬币只有正反两面。
2.硬币正反面出现的概率相同。
2.单次实验需要投掷多次硬币。

而计算机中的hash算法正好可以满足这3个条件：
1.hash结果的每一个bit只有0和1，代表硬币的正反两面。
2.如果hash算法足够好，得到的结果就足够随机，可以近似认为每一个bit的0和1产生的概率是相同的。
3.hash的结果如果是64个bit，正好代表投掷了64次硬币。

因此执行一次hash，就相当于完整地进行了一次场景3中的投币实验。按照约定，实验完成后，我们需要记录硬币投掷的结果。
假定现在有2个用户id；user1、user2
先对user1进行hash，假定得到如下8个bit的结果：
10100100
此时从右到左，我们约定0表示反面，1表示正面，于是在这次实验中，第一个为1的bit出现在第三位，相当于先投出了2次反面，然后投出1次正面，于是我们记录下这次实验的投掷次数为3。因为约定只要投出正面，当次实验就结束，所以第一个1左边的所有bit就不再考虑了。
再对user2进行hash，假定得到：
01101000
第一个为1的bit出现在第4位，于是记录下4。
对于每个用户的访问请求，我们都可以对用户的id进行hash（相当于场景3中进行一次实验），并记录下第一个为1的bit出现的位数（相当于场景3中记录下硬币的投掷次数），那么通过记录到的位数的最大值，我们就可以大概估计出一共进行了多少次实验（相当于场景3中的反向推测），也就是有多少个不同的用户发生了访问。
例如某个页面有若干个用户进行了访问，我们观察记录下的数据，发现记录下的最大值是10，就意味着hash的结果至少出现了一次右边9个bit都为0的情况。而这种情况发生的概率为1/1024，于是我们可以推测大概有1024个用户访问过该页面，才有可能出现一次这种结果。

4.redis中的具体数据结构

在本文开头，有说到redis使用了12kb的存储空间来存储hyperloglog的结果，那这12kb是如何具体分配的呢？接下去就来讨论这个部分。

redis的分桶

要使用极大似然估计，需要可观察的结果足够多，但这个“足够多”其实并没有严谨的规定，和100比1万也挺多了，但和100万比较又显得少了，况且观察结果再多，误差总是有的，一些极端情况也是有可能发生的（就像有的人可能买一次彩票就中奖了，有的人可能买一辈子也没有中过）。为了减小这种误差，redis将统计结果分散到了总计16384个桶中，在最终计算总的结果的时候，再将这每一个桶的统计结果再做一次调和平均，使得各种极端情况的影响降到最低。

数据存储结构

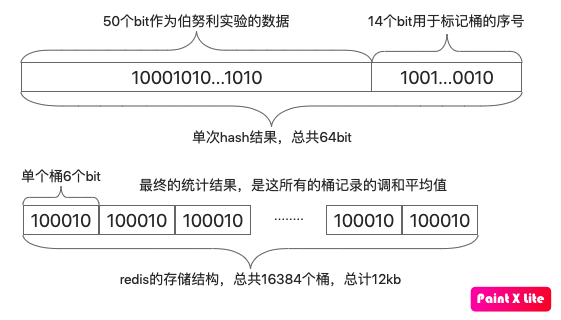
redis采用的hash算法能得到一个64bit的结果，前面讲到redis进行了分桶，于是为了确定这个hash的结果需要放到哪个桶中，就需要拿出14个bit来计算桶的序号，2的14次方正好是16384。
确定好放入哪个桶后，剩下的50个bit就作为扔硬币的实验结果，而最坏的实验结果是最左边的bit为1，其他bit都为0：10000....0000，此时我们需要记录的可能的最大数字就是50（即第一个为1的bit出现在第50位），而50的二进制是110010，需要6个bit存放。因此对于任意的hash结果，一个桶最多最多只需要6个bit就能存放下所有可能结果了
redis总共分了16384个桶，每个桶需要6bit，于是总计：$$16384\times6\div8\div1024=12kb$$
如下图：

稀疏结构与密集结构

当redis刚创建完一个hyperloglog结构的时候，其中的所有bit都为0。为了避免重复数据对存储空间的浪费，redis使用了几种特殊的数据结构来表示重复数据：
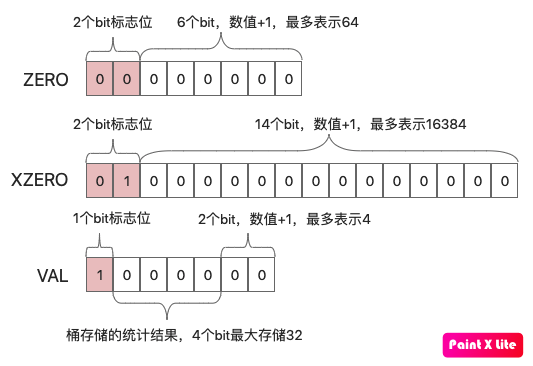
ZERO : 一字节，表示连续多少个桶计数为0，前两位为标志00，后6位表示有多少个桶，最大为64。
XZERO : 两个字节，表示连续多少个桶计数为0，前两位为标志01，后14位表示有多少个桶，最大为16384
VAL : 一字节，表示连续多少个桶的计数为多少，前一位为标志1，四位表示连桶内计数，所以最大表示桶的计数为32。后两位表示连续多少个桶。
（ZERO和XZERO的区别在于如果连续为0的桶数量小于64个的时候，就没必要用14个bit来表示数量，进一步节约空间）

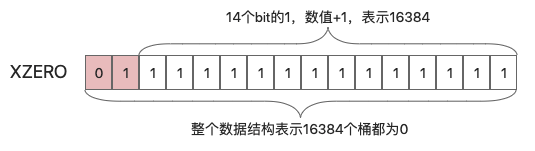
当redis创建完一个新的hyperloglog结构时，因为其中的所有bit都为0，所以并不需要实际使用12kb的空间存放16384个0，而是用2个字节的XZERO来表示：

经过用户的少数几次访问后，redis可能用如下结构存储：

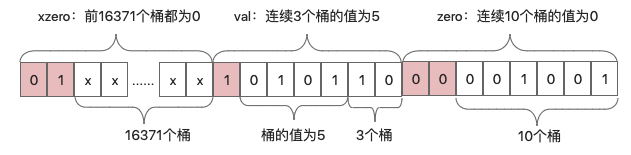
当满足如下条件时，就会从稀疏结构不可逆地变成密集结构：
1.任意一个val结构存储的值达到33，超出了能存储的最大值
2.稀疏结构的总字节数超过3000字节

最后回顾和总结一下本文的内容
1.hyperloglog适用于大数据量的去重统计
2.极大似然估计：当可观察的结果足够多时，我们可以“大概率”地推测出条件的状态。
3.伯努利实验：扔硬币
4.伯努利实验的极大似然估计：通过观察“最小概率”出现的实验结果，推测出实验进行的“大概率”次数。
5.redis通过hash算法，模拟伯努利实验，从而“大概率”推测出进行hash的次数。
6.为了减少误差，redis进行了分桶和调和平均
7.为了优化存储，redis引入了稀疏结构