双指针
关于指针的操作
int x;
int * p1 = &x; // 指针可以被修改,值也可以被修改
const int * p2 = &x; // 指针可以被修改,值不可以被修改(const int)
int * const p3 = &x; // 指针不可以被修改(* const),值可以被修改
const int * const p4 = &x; // 指针不可以被修改,值也不可以被修改
//指针函数:返回一个类型是指针的函数 int* func(int a,int b){ int* sum=new int(a+b); return sum; } //函数指针:指向函数的指针 int subtraction(int a, int b) { return a - b; } //minus就是函数指针 int (*minus)(int,int)=subtraction; int operation(int x, int y, int (*func)(int, int)) { return (*func)(x,y); }
167、
给你一个下标从 1 开始的整数数组 numbers ,该数组已按 非递减顺序排列 ,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 <= index1 < index2 <= numbers.length 。
以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。
你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
你所设计的解决方案必须只使用常量级的额外空间。
class Solution { public: vector<int> twoSum(vector<int>& numbers, int target) { int index1=0; int index2=numbers.size()-1; while(index1<index2) { if(numbers[index1]+numbers[index2]>target) index2--; if(numbers[index1]+numbers[index2]<target) index1++; if(numbers[index1]+numbers[index2]==target) return {index1+1,index2+1}; } return {-1,-1}; } };
88、
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
class Solution { public: void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) { int p1 = 0, p2 = 0; int sorted[m + n]; int cur; while (p1 < m || p2 < n) { if (p1 == m) { cur = nums2[p2++]; } else if (p2 == n) { cur = nums1[p1++]; } else if (nums1[p1] < nums2[p2]) { cur = nums1[p1++]; } else { cur = nums2[p2++]; } sorted[p1 + p2 - 1] = cur; } for (int i = 0; i != m + n; ++i) { nums1[i] = sorted[i]; } } };
142、
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
/** * Definition for singly-linked list. * struct ListNode { * int val; * ListNode *next; * ListNode(int x) : val(x), next(NULL) {} * }; */ class Solution { public: ListNode *detectCycle(ListNode *head) { ListNode* m=head,*k=head; while(k!=NULL&&k->next!=NULL) { k=k->next->next; m=m->next; if(k==m) { k=head; while(k!=m) { k=k->next; m=m->next; } return k; } } return NULL; } };
第一次出错:对快慢表理解不正确,当第一次相遇时只能确定存在环区,第二次相遇才是才是环的起点
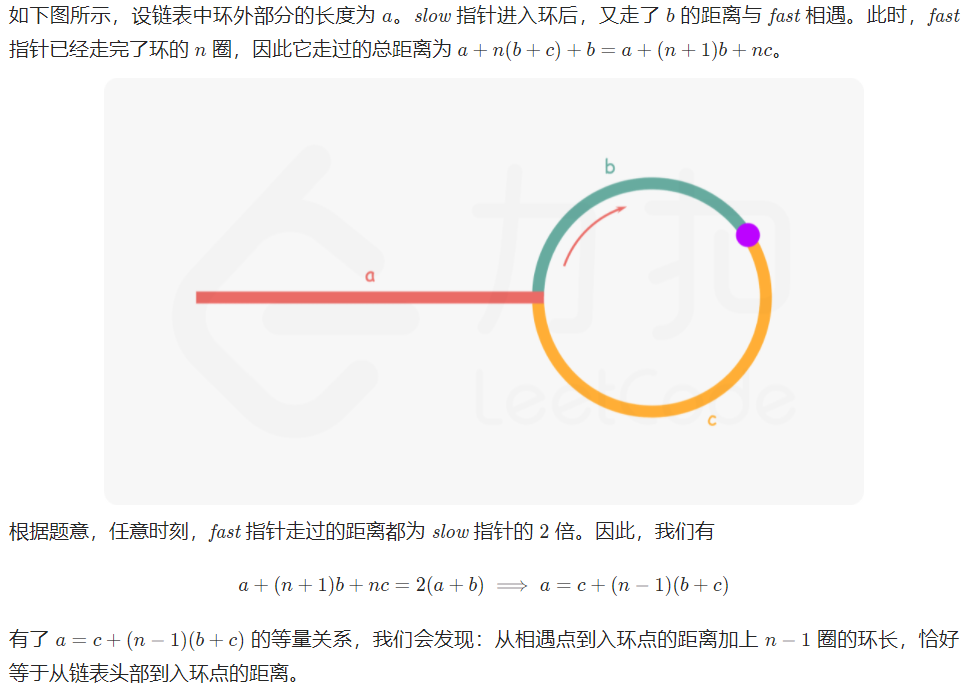
第二次出错:由于快指针一次走两个,无环情况快指针可能会访问到空指针出现错误(还有几次也是这个错误,要细心考虑不能太急躁了)
76、
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
class Solution { public: //检查hs中是否包含了ht的全部字符以及个数 bool check(unordered_map<char, int> &hs, unordered_map<char, int> &ht){ for(unordered_map<char,int>::iterator it=ht.begin();it!=ht.end();it++){ if(hs[it->first]<it->second){ return false; } } return true; } string minWindow(string s, string t) { unordered_map<char, int> hs; //用于保存字符串s的滑动窗口里元素出现次数 unordered_map<char, int> ht; //保存字符串t中各元素出现次数 int minlen = INT_MAX; //记录最小长度 int ansL = -1; //子串的左边起点 for(int i=0;i<t.size();i++) ht[t[i]]++; //遍历t,并统计各字符出现次数 //滑动窗口,让k不断往右移动,找到一个满足条件的子串 for(int i=0,j=0;i<=j&&j<s.size();){ //如果滑动窗口内元素是空的并且j所指元素不在ht中,可以让i和j都先右移,直到碰见第一个元素在ht里面 if(hs.empty()&&ht.find(s[j])==ht.end()){ i++; j++; } //如果j处元素在ht中有,那么j处元素也需要保存到hs中 if(ht.find(s[j])!=ht.end()) hs[s[j]]++; //往hs里面填充有效元素,非必要的不要放进去 //如果此时hs已经包含了ht中全部字符,就需要让i往右移 while(check(hs,ht)&&i<=j){ //如果当前子串长度更小,则更新 if(j-i+1<minlen){ minlen = j-i+1; ansL = i; //记录起点 } //如果i处元素在ht中有,将出现hs中对应出现次数-1 if(ht.find(s[i])!=ht.end()) hs[s[i]]--; //元素出现次数减1 i++; //i往右移 } j++; //j继续右移 } if(ansL==-1) return ""; else{ return s.substr(ansL, minlen); } } };
可以想到利用滑动窗口确定范围,但不知道怎么确定范围中的字符是否存在。
此代码和以下解析来源于作者:traveller-lzx。
利用滑动窗口的思想,不断更新窗口的左边界和右边界;
利用哈希表ht保存t中所有的元素和对应出现次数,哈希表hs保存滑动窗口中出现的有效元素(就是该元素在t/ht中出现过的元素)及对应出现次数;
让窗口的右边界j不断右移,直到窗口内的有效元素hs集合中元素出现次数>=ht中相应元素出现次数,此时让窗口左边界i开始向右缩小,并逐个剔除元素,直到窗口不能再缩小为止,保存此时窗口内有效子串的长度为minlen,并记录该子串的起点为ansL;
循环迭代上述过程,最后利用substr()函数,返回子串即可;
优化思路:
此代码基本按照官方的题解思路进行编写,有以下几个细节需要注意:
刚开始当还没有建立滑动窗口时,可能j指针会指向很多无效元素,例如"s=xxxABCxx,t=ABC",我们可以让i和j一开始先跳过前面的xxx,具体看代码实现;
哈希表hs需要存放有效元素(就是该元素在t/ht中出现过的元素),而不是每遍历一个元素,都要存进去,这样会浪费内存,最后不一定能通过;
check()函数里传递参数用引用传递的方式,如果是拷贝构造,可能会因为数据量过大,最后一个测试用例过不了;
更新res子串并不需要在调整窗口左边界的过程中进行,而是用子串长度minlen和子串起始位置ansL来记录即可,更新记录,最后再用substr()返回;
代码
作者:traveller-lzx
链接:https://leetcode-cn.com/problems/minimum-window-substring/solution/zui-xiao-fu-gai-zi-chuan-hua-dong-chuang-fado/
来源:力扣(LeetCode)
633、给定一个非负整数 c ,你要判断是否存在两个整数 a 和 b,使得 a2 + b2 = c 。
class Solution { public: bool judgeSquareSum(int c) { long a,b; if(c==0) return true; b=long(sqrt(c)); a=0; while(a<=b) { if(a*a+b*b==c) return true; else if(a*a+b*b>c) b--; else if(a*a+b*b<c) a++; } return false; } };
双指针的思想,出了点小问题,因为给的范围比较大,所以用int类型有可能溢出,换成了long。
一开始有点丢脸,想写开方结果写成了取对数。
680、
class Solution { public: bool validPalindrome(string s) { int i,j; i=0,j=s.size()-1; while(i<j) { if(s[i]==s[j]) { i++;j--; } else return deleteString(s,i+1,j)||deleteString(s,i,j-1); } return true; } bool deleteString(string s,int left,int right) { while(left<right) { if(s[left]==s[right]) { left++;right--; } else return false; } return true; } };
没有考虑到删任意边同时满足两边一致的情况,比如这个用例"cuppucu"如果先删左边,虽然删的时候满足了条件,但返回的时候是false,如果先删右边则是true.
上面 deleteString(s,i+1,j)||deleteString(s,i,j-1),判断两种情况,只要有一种成功,便返回true。




