环套圆的二维样本点如何实现全连接网络分类
1,数据生成
import random
import numpy as np
from matplotlib import pyplot as plt
aList = []
num1 = 0
bList = []
num2 = 0
for i in range(1000):
point = [random.random()*2-1, random.random()*2-1]
if point[0]**2+point[1]**2 <= 1/9 and num1<=100:
aList.append(point)
num1+=1
elif 4/9<=point[0]**2+point[1]**2<=1 and num2<=100:
bList.append(point)
num2+=1
a = np.array(aList)
b = np.array(bList)
a = np.concatenate((a, np.ones([np.shape(a)[0], 1])), axis=1)
b = np.concatenate((b, np.zeros([np.shape(b)[0], 1])), axis=1)
c = np.concatenate((a,b), axis=0)
np.savetxt('a.txt', a)
np.savetxt('b.txt', b)
np.savetxt('c.txt', c)
plt.scatter(a[:,0], a[:,1], c='r')
plt.scatter(b[:,0], b[:,1], c='b')
plt.show()
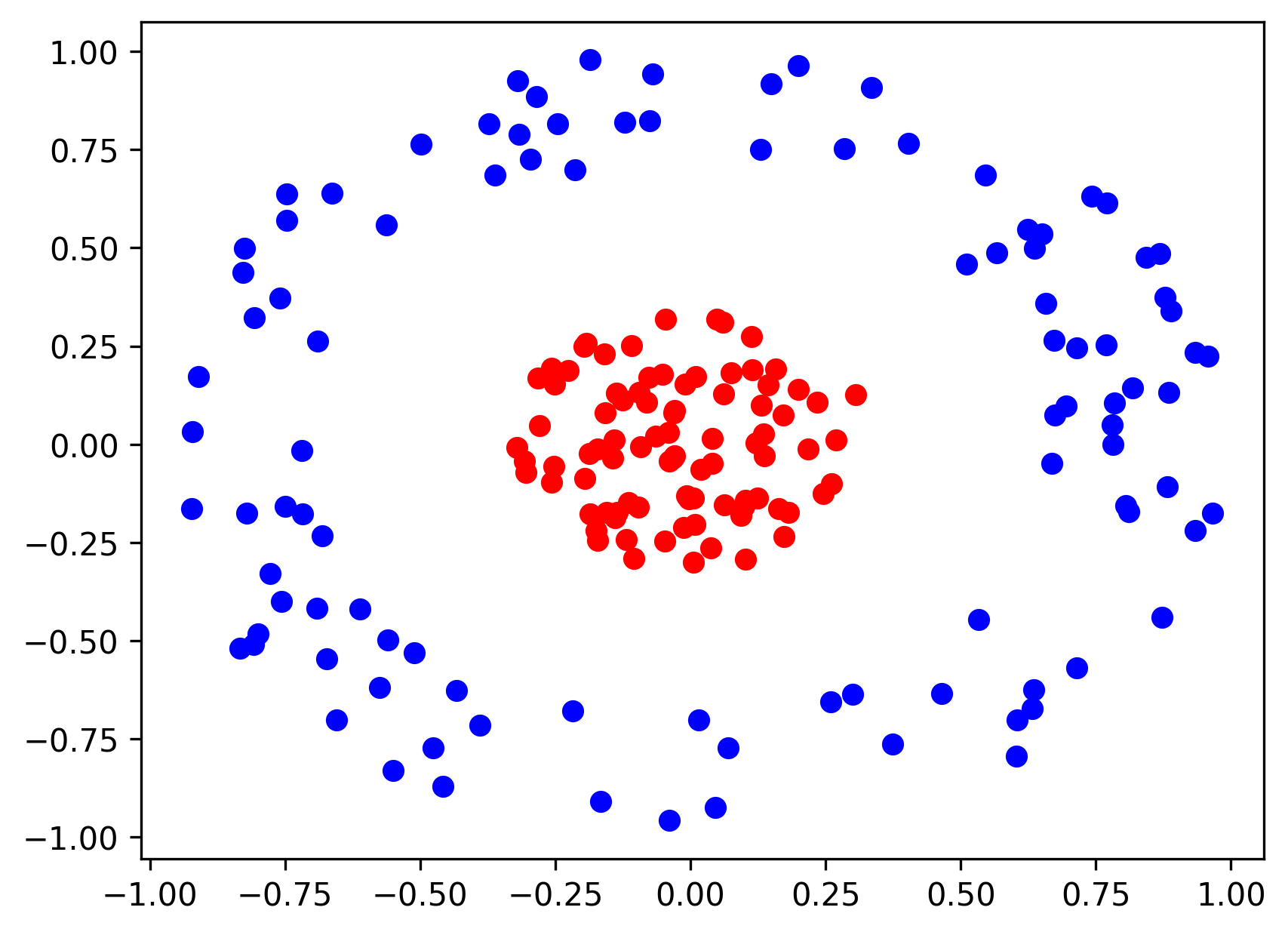
2,模型1:
import numpy as np
import torch
import torch.nn as nn
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
from tqdm import tqdm
from matplotlib import pyplot as plt
#1,准备数据集
data = np.loadtxt('c.txt')
class dataDataset(Dataset):
def __init__(self):
self.data = torch.tensor(data, dtype=torch.float)
def __len__(self):
return self.data.shape[0]
def __getitem__(self, index):
return self.data[index, :2], self.data[index, 2]
totalDataset = dataDataset()
total_dataloader = DataLoader(totalDataset, batch_size=20, shuffle=True)
#2,三要素:假设空间、评价指标、优化算法
net = nn.Sequential(nn.Linear(2,2), nn.Tanh(), nn.Linear(2,2), nn.Tanh(), nn.Linear(2,2), nn.Tanh(), nn.Linear(2,2), nn.Tanh(), nn.Linear(2,1)).cuda()
loss = nn.PairwiseDistance(p=2)
optimizer = torch.optim.Adam(net.parameters())
#3,零碎:学习率,更新代数
epoch = 100
for i in tqdm(range(epoch)):
for data, label in total_dataloader:
optimizer.zero_grad()
loss(label.cuda(), net(data.cuda())).mean().backward()
optimizer.step()
changedA = net[:-1](torch.tensor(np.loadtxt('a.txt')[:,:2],dtype=torch.float).cuda()).detach().cpu().numpy()
print(net(torch.tensor(np.loadtxt('a.txt')[:,:2],dtype=torch.float).cuda())[:10])
changedB = net[:-1](torch.tensor(np.loadtxt('b.txt')[:,:2],dtype=torch.float).cuda()).detach().cpu().numpy()
print(net(torch.tensor(np.loadtxt('b.txt')[:,:2],dtype=torch.float).cuda())[:10])
plt.scatter(changedA[:,0], changedA[:,1], c='r')
plt.scatter(changedB[:,0], changedB[:,1], c='b')
plt.savefig('模型1.png', dpi=300, bbox_inches='tight')
plt.show()
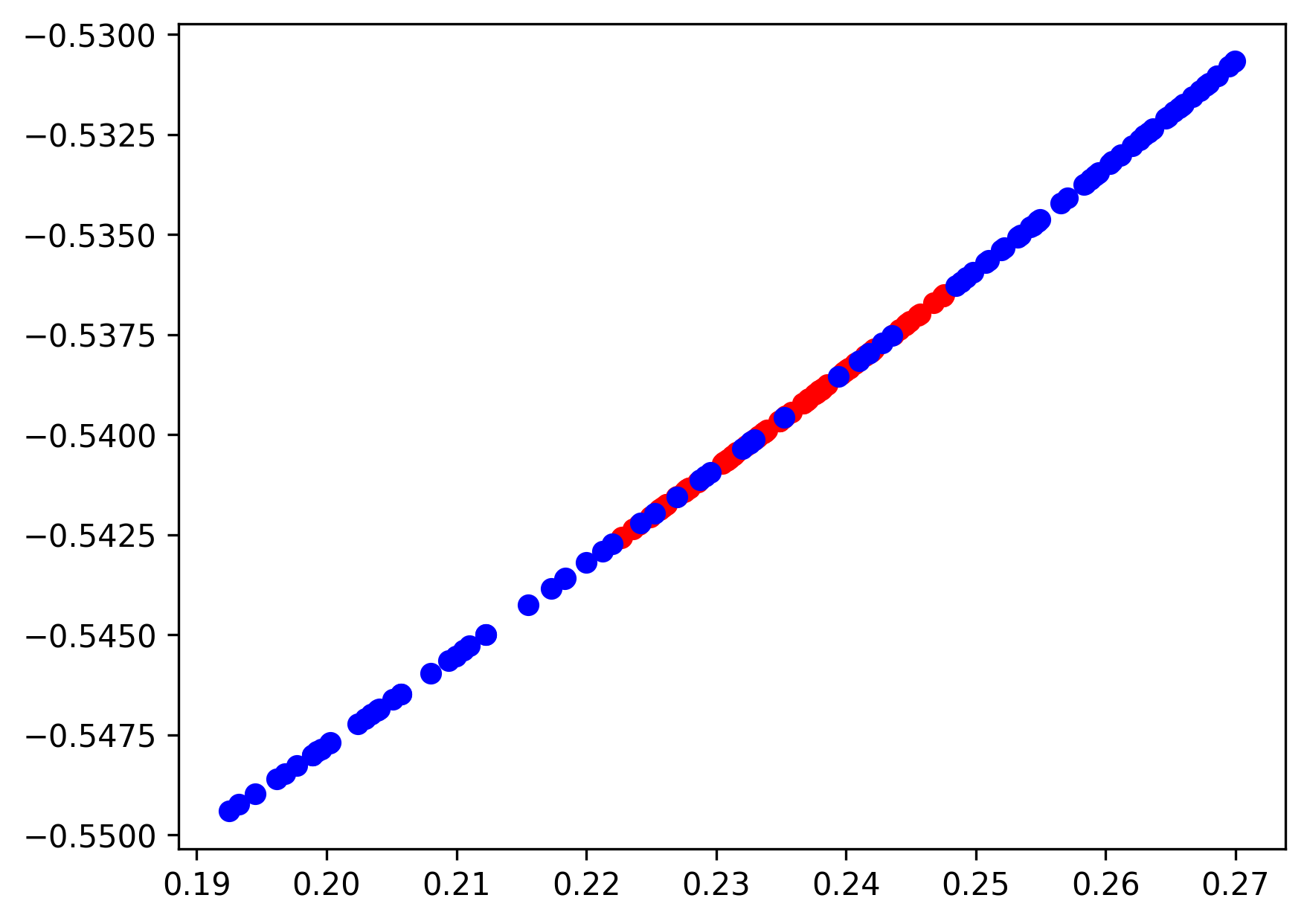
3,模型2:
import numpy as np
import torch
import torch.nn as nn
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
from tqdm import tqdm
from matplotlib import pyplot as plt
#1,准备数据集
data = np.loadtxt('c.txt')
class dataDataset(Dataset):
def __init__(self):
self.data = torch.tensor(data, dtype=torch.float)
def __len__(self):
return self.data.shape[0]
def __getitem__(self, index):
return self.data[index, :2], self.data[index, 2]
totalDataset = dataDataset()
total_dataloader = DataLoader(totalDataset, batch_size=20, shuffle=True)
#2,三要素:假设空间、评价指标、优化算法
net = nn.Sequential(nn.Linear(2,3), nn.Tanh(), nn.Linear(3,3), nn.Tanh(), nn.Linear(3,3), nn.Tanh(), nn.Linear(3,3), nn.Tanh(), nn.Linear(3,1)).cuda()
loss = nn.PairwiseDistance(p=2)
optimizer = torch.optim.Adam(net.parameters())
#3,零碎:学习率,更新代数
epoch = 100
for i in tqdm(range(epoch)):
for data, label in total_dataloader:
# print(label)
optimizer.zero_grad()
l = loss(label.cuda(), net(data.cuda())).mean()
print(l)
l.backward()
optimizer.step()
changedA = net[:-1](torch.tensor(np.loadtxt('a.txt')[:,:2],dtype=torch.float).cuda()).detach().cpu().numpy()
print(net(torch.tensor(np.loadtxt('a.txt')[:,:2],dtype=torch.float).cuda())[:10])
changedB = net[:-1](torch.tensor(np.loadtxt('b.txt')[:,:2],dtype=torch.float).cuda()).detach().cpu().numpy()
print(net(torch.tensor(np.loadtxt('b.txt')[:,:2],dtype=torch.float).cuda())[:10])
fig = plt.figure(figsize=(12,6))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(changedA[:, 0], changedA[:, 1],changedA[:,2],c="r")
ax.scatter(changedB[:, 0], changedB[:, 1],changedB[:,2],c="b")
plt.grid(True)
plt.savefig('模型2.png', dpi=300, bbox_inches='tight')
plt.show()
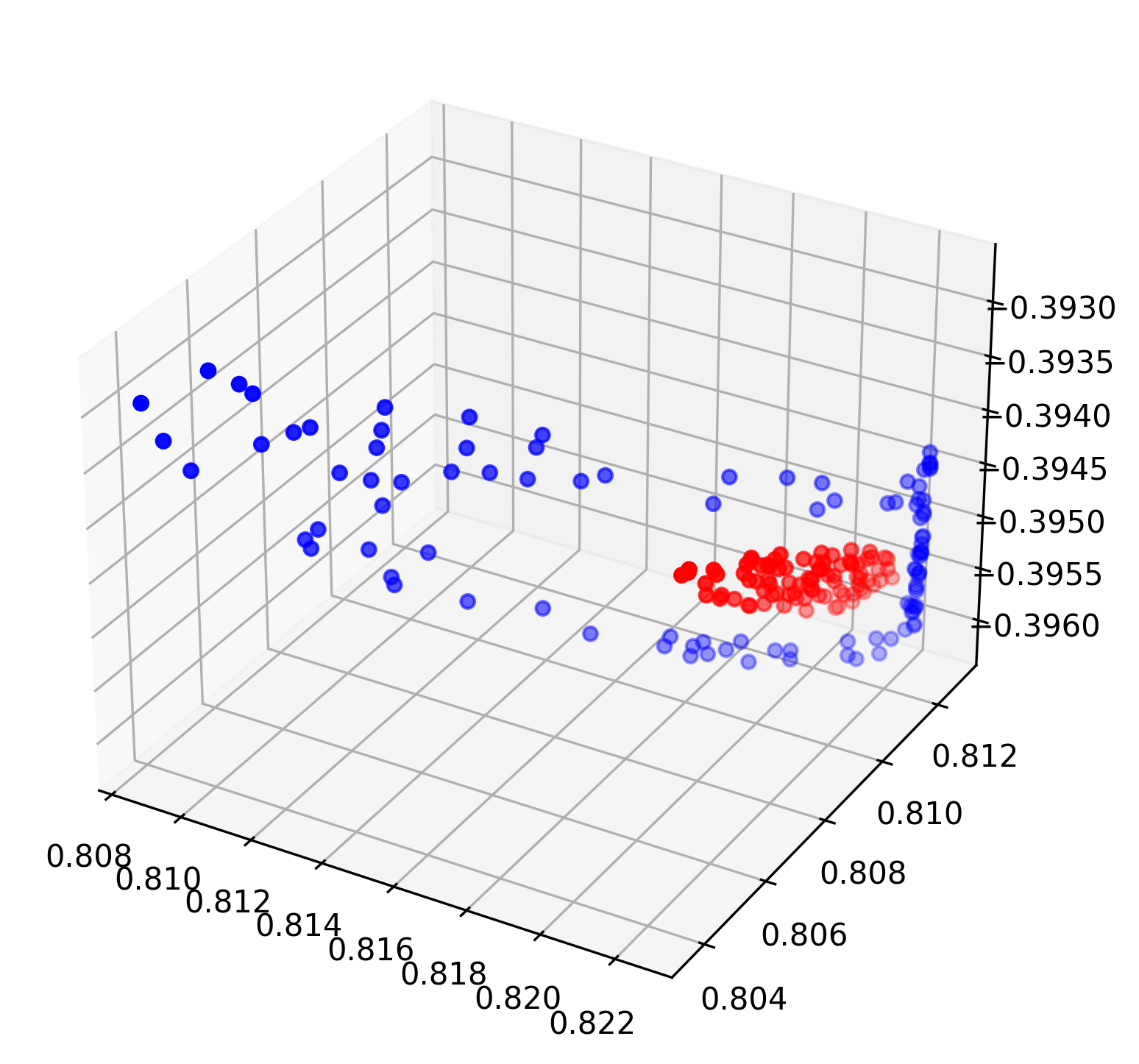
4,模型2的问题:
- 线性变换没有升维作用(强转高维依旧是低维流形),这里模型2使用线性函数与非线性激活函数的组合没有成功分开,只是模型不够宽以及损失函数没有用对。
5,模型3:
import numpy as np
import torch
import torch.nn as nn
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
from tqdm import tqdm
from matplotlib import pyplot as plt
#1,准备数据集
data = np.loadtxt('c.txt')
#1.1,数据升维
def dimensionIncreasion(dataset):
res = []
for data in dataset:
middle = []
middle.append(data[0])
middle.append(data[1])
middle.append(data[0]**2 + data[1]**2)
middle.append(data[2])
res.append(middle)
return np.array(res)
data = dimensionIncreasion(data)
class dataDataset(Dataset):
def __init__(self):
self.data = torch.tensor(data, dtype=torch.float)
def __len__(self):
return self.data.shape[0]
def __getitem__(self, index):
return self.data[index, :-1], self.data[index, -1]
totalDataset = dataDataset()
total_dataloader = DataLoader(totalDataset, batch_size=20, shuffle=True)
#2,三要素:假设空间、评价指标、优化算法
net = nn.Sequential(nn.Linear(3,3), nn.ReLU(), nn.Linear(3,1)).cuda()
loss = nn.PairwiseDistance(p=2)
optimizer = torch.optim.Adam(net.parameters())
#3,零碎:学习率,更新代数
epoch = 100
for i in tqdm(range(epoch)):
for data, label in total_dataloader:
print(label)
optimizer.zero_grad()
l = loss(label.cuda(), net(data.cuda())).mean()
# print(l)
l.backward()
optimizer.step()
dataA = dimensionIncreasion(np.loadtxt('a.txt'))
dataB = dimensionIncreasion(np.loadtxt('b.txt'))
changedA = net[:-1](torch.tensor(dataA[:,:-1],dtype=torch.float).cuda()).detach().cpu().numpy()
print(net(torch.tensor(dataA[:,:-1],dtype=torch.float).cuda())[:10])
changedB = net[:-1](torch.tensor(dataB[:,:-1],dtype=torch.float).cuda()).detach().cpu().numpy()
print(net(torch.tensor(dataB[:,:-1],dtype=torch.float).cuda())[:10])
fig = plt.figure(0, figsize=(12,6))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(dataA[:, 0], dataA[:, 1],dataA[:,2],c="r")
ax.scatter(dataB[:, 0], dataB[:, 1],dataB[:,2],c="b")
plt.grid(True)
plt.savefig('模型3-0.png', dpi=300, bbox_inches='tight')
fig = plt.figure(1, figsize=(12,6))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(changedA[:, 0], changedA[:, 1],changedA[:,2],c="r")
ax.scatter(changedB[:, 0], changedB[:, 1],changedB[:,2],c="b")
plt.grid(True)
plt.savefig('模型3-1.png', dpi=300, bbox_inches='tight')
plt.show()
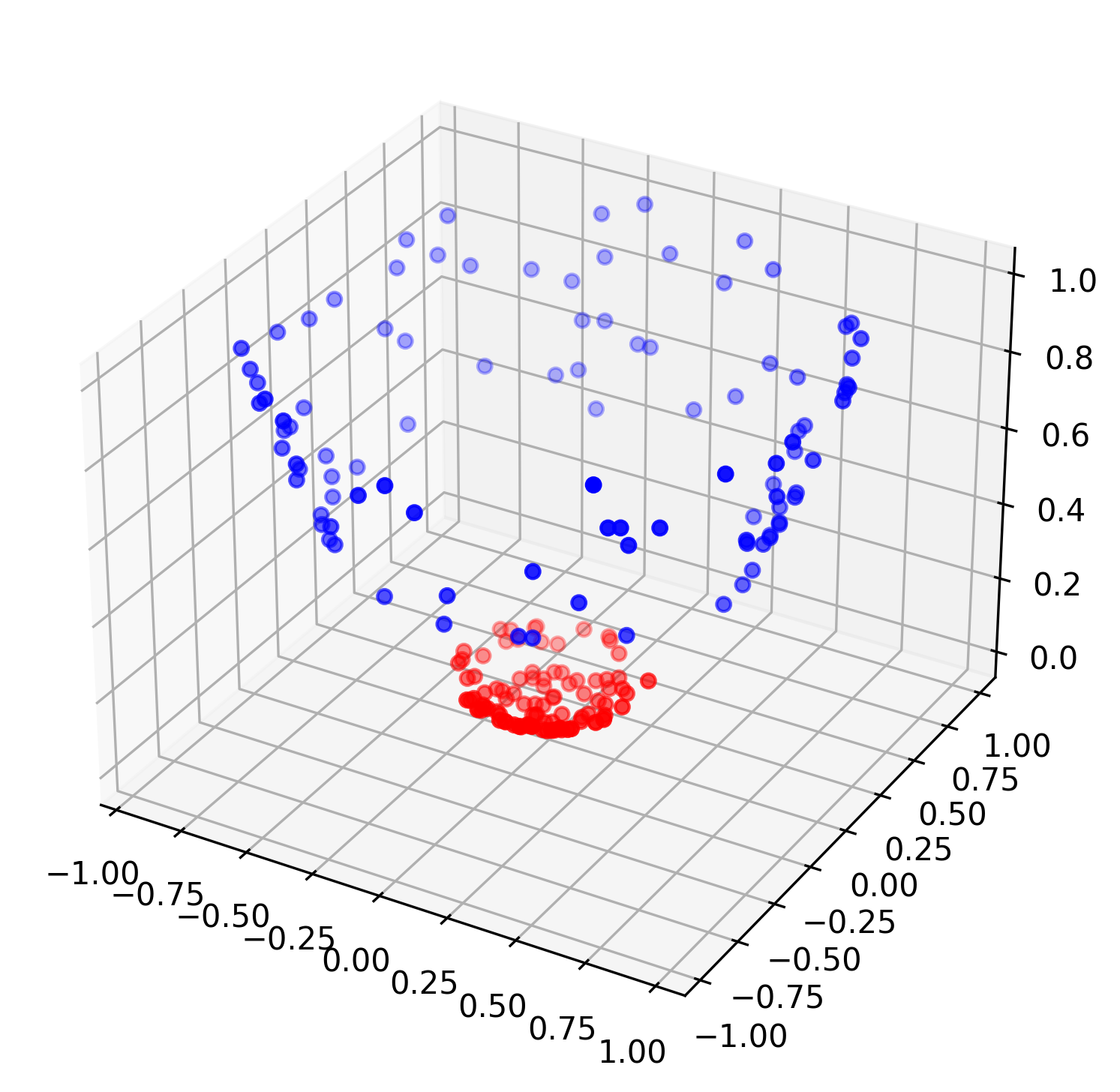
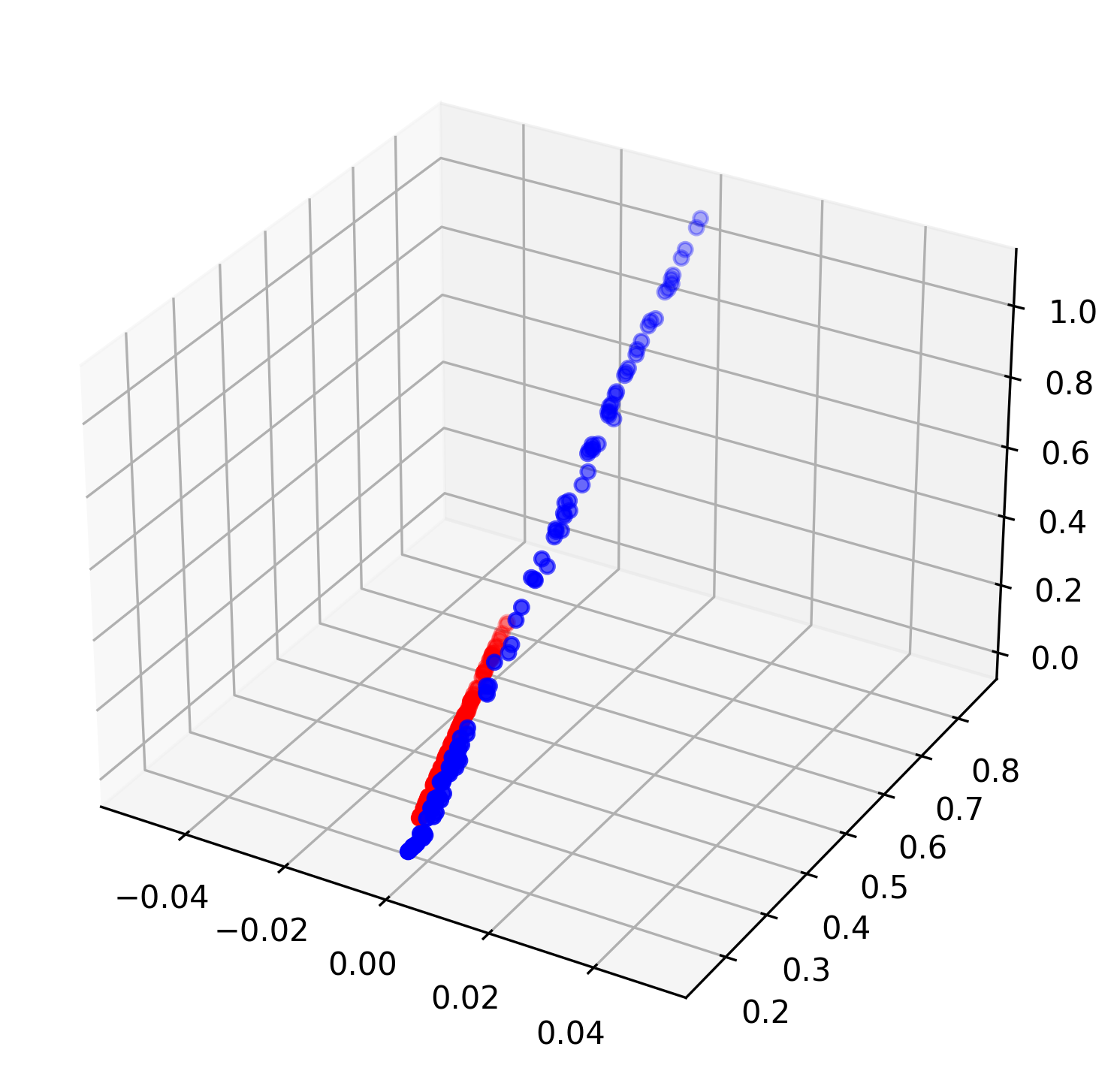
6,模型3的问题:
- 通过非线性变换人为将数据升到3维,可以很明显的看出数据此时在3维空间是线性可分的,但是结果依旧很差,这里的问题出在损失函数上。nn.PairwiseDistance()等距离度量型损失函数直接用于分类相当于将所有的数据样本映射到同一个值,这不是一个[3,3],[3,1]矩阵可以做到的。(这纯粹是记录样本信息,并将各样本进行值的映射,甚至算不上是数据挖掘)
7,模型3的改进:
- 使用nn.CrossEnrtopyLoss()等交叉熵损失函数,包含不定阈值划分,将同类数据样本映射到一个区域(区间)
import numpy as np
import torch
import torch.nn as nn
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
from tqdm import tqdm
from matplotlib import pyplot as plt
#1,准备数据集
data = np.loadtxt('c.txt')
#1.1,数据升维
def dimensionIncreasion(dataset):
res = []
for data in dataset:
middle = []
middle.append(data[0])
middle.append(data[1])
middle.append(data[0]**2 + data[1]**2)
middle.append(data[2])
res.append(middle)
return np.array(res)
data = dimensionIncreasion(data)
class dataDataset(Dataset):
def __init__(self):
self.data = torch.tensor(data, dtype=torch.float)
def __len__(self):
return self.data.shape[0]
def __getitem__(self, index):
return self.data[index, :-1], self.data[index, -1]
totalDataset = dataDataset()
total_dataloader = DataLoader(totalDataset, batch_size=20, shuffle=True)
#2,三要素:假设空间、评价指标、优化算法
net = nn.Sequential(nn.Linear(3,3), nn.ReLU(), nn.Linear(3,2)).cuda()
loss = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters())
#3,零碎:学习率,更新代数
epoch = 100
for i in tqdm(range(epoch)):
for data, label in total_dataloader:
print(label)
optimizer.zero_grad()
l = loss(net(data.cuda()), label.cuda().to(torch.long)).mean()
# print(l)
l.backward()
optimizer.step()
dataA = dimensionIncreasion(np.loadtxt('a.txt'))
dataB = dimensionIncreasion(np.loadtxt('b.txt'))
changedA = net[:-1](torch.tensor(dataA[:,:-1],dtype=torch.float).cuda()).detach().cpu().numpy()
print(net(torch.tensor(dataA[:,:-1],dtype=torch.float).cuda())[:10])
changedB = net[:-1](torch.tensor(dataB[:,:-1],dtype=torch.float).cuda()).detach().cpu().numpy()
print(net(torch.tensor(dataB[:,:-1],dtype=torch.float).cuda())[:10])
fig = plt.figure(0, figsize=(12,6))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(dataA[:, 0], dataA[:, 1],dataA[:,2],c="r")
ax.scatter(dataB[:, 0], dataB[:, 1],dataB[:,2],c="b")
plt.grid(True)
plt.savefig('模型3-0.png', dpi=300, bbox_inches='tight')
fig = plt.figure(1, figsize=(12,6))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(changedA[:, 0], changedA[:, 1],changedA[:,2],c="r")
ax.scatter(changedB[:, 0], changedB[:, 1],changedB[:,2],c="b")
plt.grid(True)
plt.savefig('模型3-1.png', dpi=300, bbox_inches='tight')
plt.show()
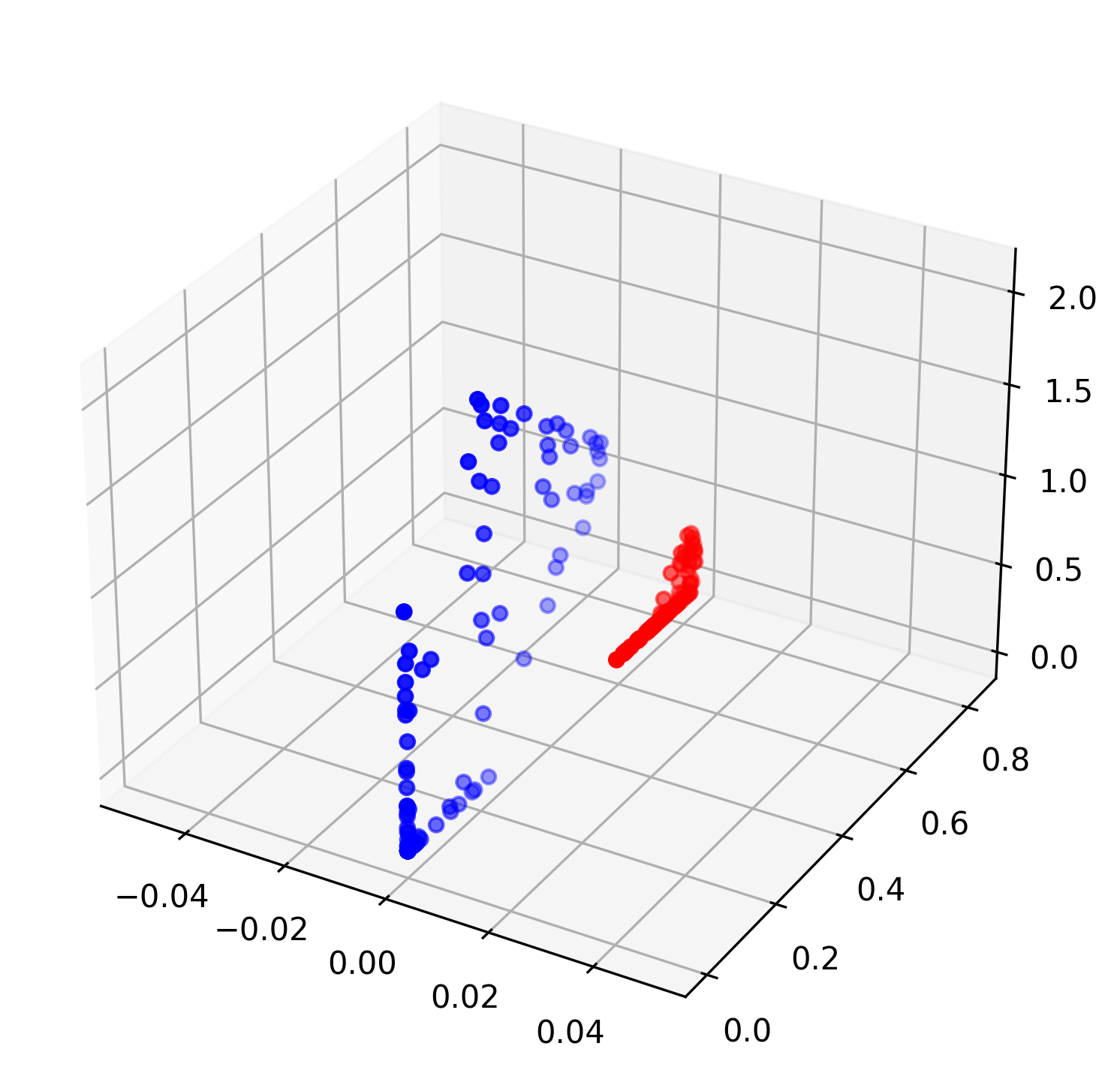
8,一个问题:
- 如果加上非线性激活函数,怎样的线性变换和非线性激活函数的组合可以起到与人为的非线性变换类似的效果?
9,模型2的改进:
import numpy as np
import torch
import torch.nn as nn
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
from tqdm import tqdm
from matplotlib import pyplot as plt
#1,准备数据集
data = np.loadtxt('c.txt')
class dataDataset(Dataset):
def __init__(self):
self.data = torch.tensor(data, dtype=torch.float)
def __len__(self):
return self.data.shape[0]
def __getitem__(self, index):
return self.data[index, :2], self.data[index, 2]
totalDataset = dataDataset()
total_dataloader = DataLoader(totalDataset, batch_size=20, shuffle=True)
#2,三要素:假设空间、评价指标、优化算法
net = nn.Sequential(nn.Linear(2,6), nn.Tanh(), nn.Linear(6,6), nn.Tanh(), nn.Linear(6,3), nn.Linear(3,2)).cuda() #可以尝试改变这里的6,进行随意取值,观察不同的结果。
loss = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters())
#3,零碎:学习率,更新代数
epoch = 100
for i in tqdm(range(epoch)):
for data, label in total_dataloader:
# print(label)
optimizer.zero_grad()
l = loss(net(data.cuda()), label.cuda().to(torch.long)).mean()
print(l)
l.backward()
optimizer.step()
changedA = net[:-1](torch.tensor(np.loadtxt('a.txt')[:,:2],dtype=torch.float).cuda()).detach().cpu().numpy()
print(net(torch.tensor(np.loadtxt('a.txt')[:,:2],dtype=torch.float).cuda())[:10])
changedB = net[:-1](torch.tensor(np.loadtxt('b.txt')[:,:2],dtype=torch.float).cuda()).detach().cpu().numpy()
print(net(torch.tensor(np.loadtxt('b.txt')[:,:2],dtype=torch.float).cuda())[:10])
fig = plt.figure(figsize=(12,6))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(changedA[:, 0], changedA[:, 1],changedA[:,2],c="r")
ax.scatter(changedB[:, 0], changedB[:, 1],changedB[:,2],c="b")
plt.grid(True)
plt.savefig('模型2.png', dpi=300, bbox_inches='tight')
plt.show()
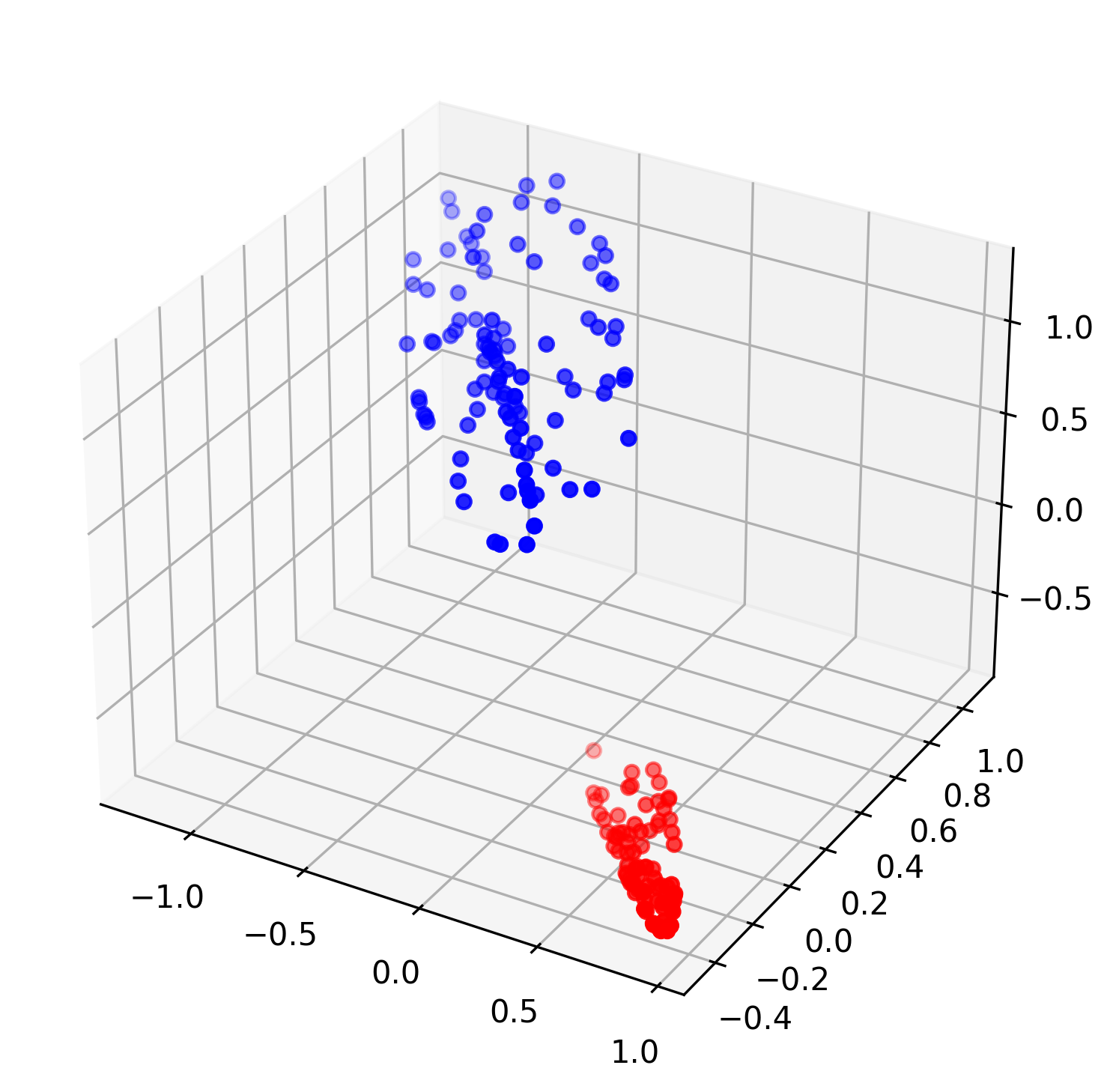
10,一个问题:
- 如果一直不升维,使用线性变换和非线性激活函数的组合可以做到可分吗?
11,模型1的改进:
- 似乎很难
import numpy as np
import torch
import torch.nn as nn
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
from tqdm import tqdm
from matplotlib import pyplot as plt
#1,准备数据集
data = np.loadtxt('c.txt')
class dataDataset(Dataset):
def __init__(self):
self.data = torch.tensor(data, dtype=torch.float)
def __len__(self):
return self.data.shape[0]
def __getitem__(self, index):
return self.data[index, :2], self.data[index, 2]
totalDataset = dataDataset()
total_dataloader = DataLoader(totalDataset, batch_size=20, shuffle=True)
#2,三要素:假设空间、评价指标、优化算法
net = nn.Sequential(nn.Linear(2,2), nn.Tanh(), nn.Linear(2,2), nn.Tanh(), nn.Linear(2,2), nn.Tanh(), nn.Linear(2,2), nn.Tanh(), nn.Linear(2,2), nn.Linear(2,2), nn.Tanh(), nn.Linear(2,2), nn.Tanh(), nn.Linear(2,2), nn.Tanh(), nn.Linear(2,2), nn.Tanh(), nn.Linear(2,2)).cuda()
loss = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters())
#3,零碎:学习率,更新代数
epoch = 100
for i in tqdm(range(epoch)):
for data, label in total_dataloader:
optimizer.zero_grad()
loss(net(data.cuda()), label.cuda().to(torch.long)).mean().backward()
optimizer.step()
changedA = net[:-1](torch.tensor(np.loadtxt('a.txt')[:,:2],dtype=torch.float).cuda()).detach().cpu().numpy()
print(net(torch.tensor(np.loadtxt('a.txt')[:,:2],dtype=torch.float).cuda())[:10])
changedB = net[:-1](torch.tensor(np.loadtxt('b.txt')[:,:2],dtype=torch.float).cuda()).detach().cpu().numpy()
print(net(torch.tensor(np.loadtxt('b.txt')[:,:2],dtype=torch.float).cuda())[:10])
plt.scatter(changedA[:,0], changedA[:,1], c='r')
plt.scatter(changedB[:,0], changedB[:,1], c='b')
plt.savefig('模型1.png', dpi=300, bbox_inches='tight')
plt.show()
总结:
- 非线性变换可以由线性变换以及非线性激活函数的组合进行模拟
- 维度变换:
- 低维无法线性可分的问题,升到高维后可以线性可分;
- 低维复杂的非线性现象只是高维线性现象在低维的投影;
- 由低维到高维这一升维过程,体现在坐标点维度的提升;由高维到低维这一过程,体现为坐标点的某些维度被移除。
- 损失函数:
- nn.PairwiseDistance(),nn.L1Loss(),nn.MSELoss()等欧式度量距离损失函数,如果直接用于分类,相当于将所有的数据样本映射到同一个值,这并不合理。
- nn.CrossEnrtopyLoss()等交叉熵损失函数,是将数据映射到C维向量,并根据相对大小进行比较(不定阈值),相当于将所有的数据样本映射到一个区域,该区域内的样本是同类的。
参考:
(透彻理解高斯核函数背后的哲学思想与数学思想)[https://blog.csdn.net/weixin_42137700/article/details/86756365]
行动是治愈恐惧的良药,而犹豫拖延将不断滋养恐惧。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号